@
目录1.图的概念
- 图的组成部分
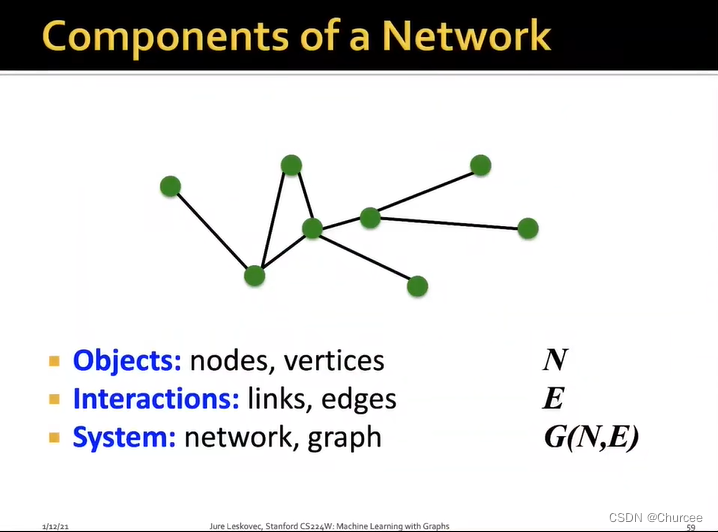
- 图的意义
作为一种解决问题的通用语言,将问题抽象成图,用同一种机器学习的算法可以求解多个问题。
但为问题选择合适的表示是很难的问题——选择合适的点、边和问题域
2.design choice
- 有向图和无向图directed/undirected graphs
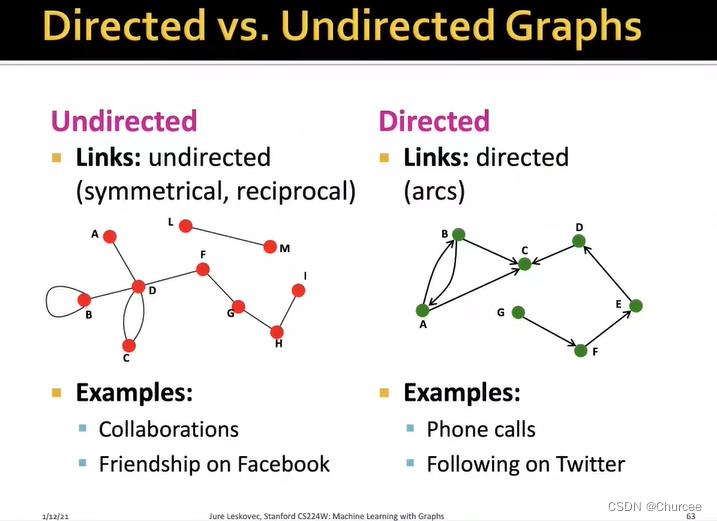
- 节点度node degrees
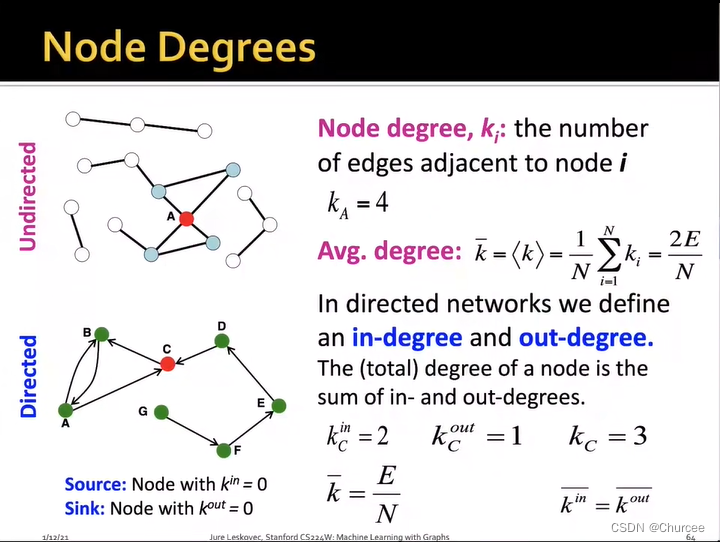
- 无向图的每个节点都被计算两次,平均节点度*2
- 自循环的无向图,增加一个节点会增加两个节点度
- 有向图分为入度in-degree和出度out-degree
- 如节点B,在无向图中节点度为2,在有向图中节点度为3
- 二部图bipartite graph
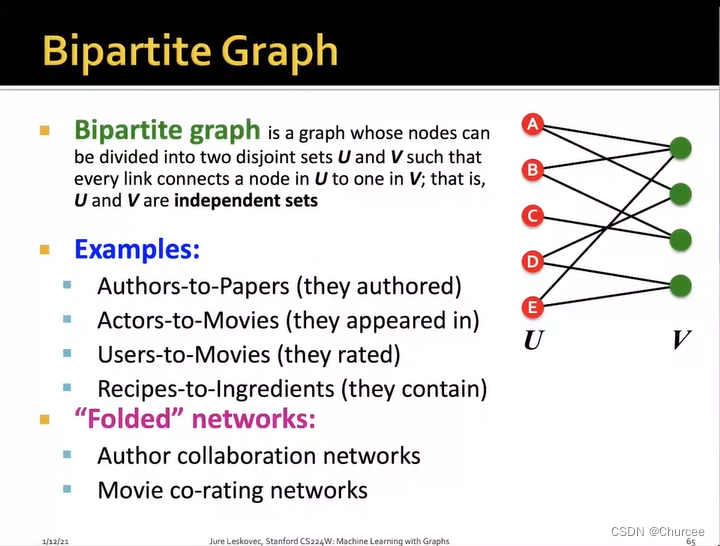
- 通常有两种不同类型的节点,其中,A类型的节点只与B类型的节点进行交互且图的边仅从左侧开始
- 折叠网络即是里面一种节点类型所建的单独的网络
- 基于此,还可以类推出多部图multipartite
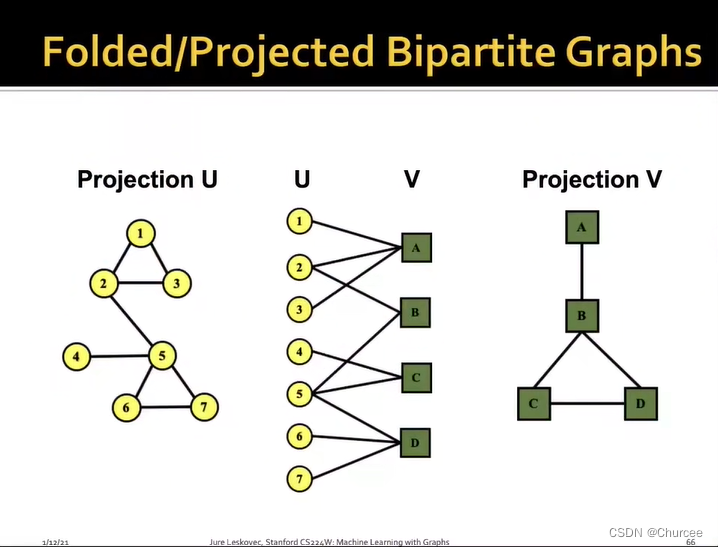
如上图,是作者U和文章V的图,当作者1,2,3一起写了文章A,那作者图里1,2,3即存在连边。所以,当我们有了二分图,可以将其投影到左侧或右侧。
3.图的表示representing graphs
- 使用邻接矩阵adjacency matrix
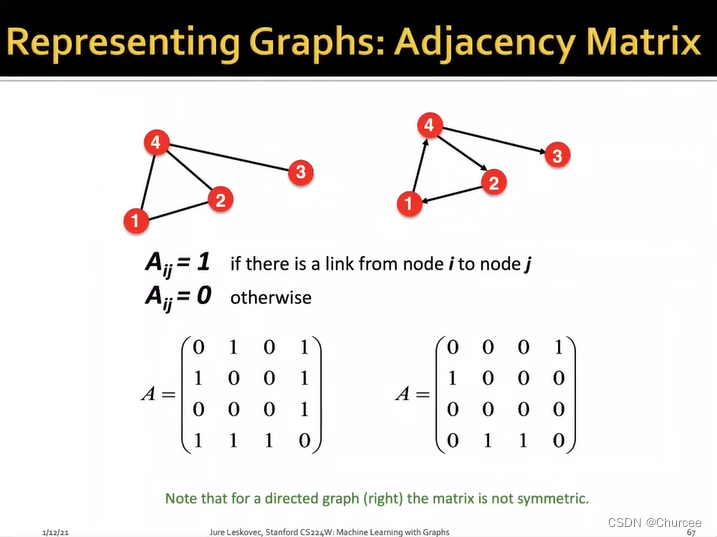
采用0-1两种选择,当两个节点间有边时,权重为1,否则权重为0.
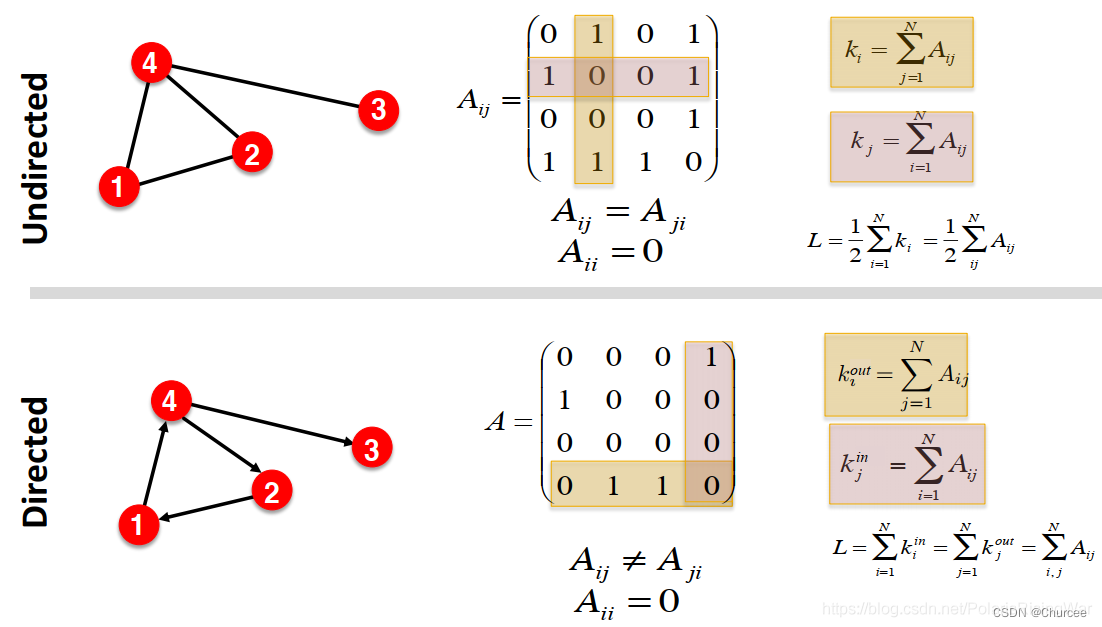
无向图和有向图邻接矩阵在路径上的区别。

大多数的网络是稀疏的sparse,如:电网power-girds、互联网连接internet connection等 - 使用边列表egde list——在深度学习中很受欢迎
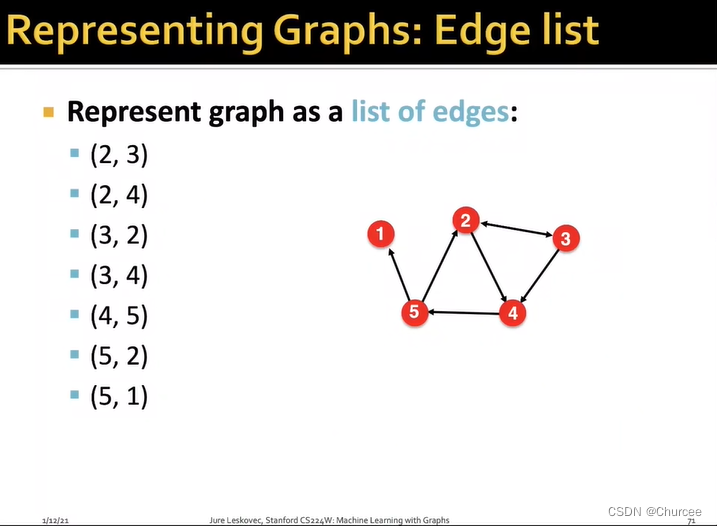
将两个节点之间的连接表示为二维矩阵two-dimensional matrix,常用于深度学习框架中,问题在于很难进行图的操作和分析,就算只是计算图中点的度数都会很难 - 使用邻接表adjacency list——便于进行图分析和处理graph analysis and mainpulation

- 适用于大型和稀疏矩阵
- 能够快读检索给定节点的所有邻边
4.图的附加属性property/attributes

- 节点的重量——可以用邻接矩阵表示
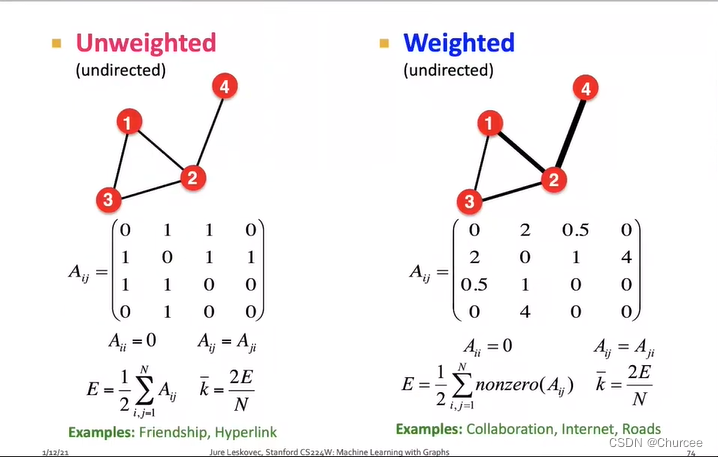
节点的重量可以表示两个节点连接的强度 - 自环和多图
具有自环的节点:如节点4的度为3
多图:一对节点间可以有多条边
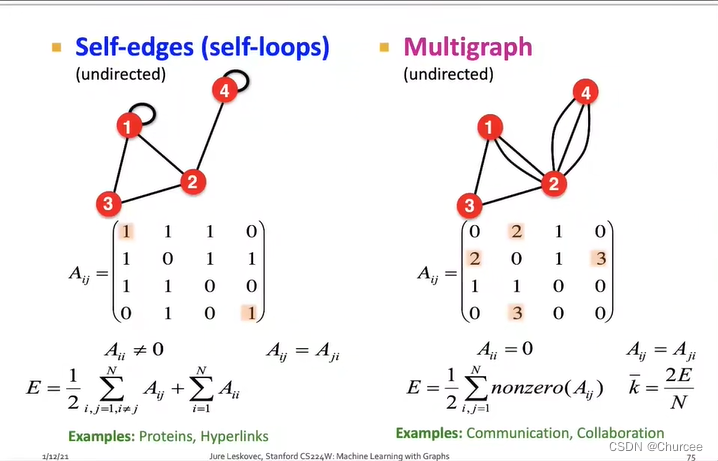
- 图的连通性connectivity of undirected graphs
- 无向图的连通性
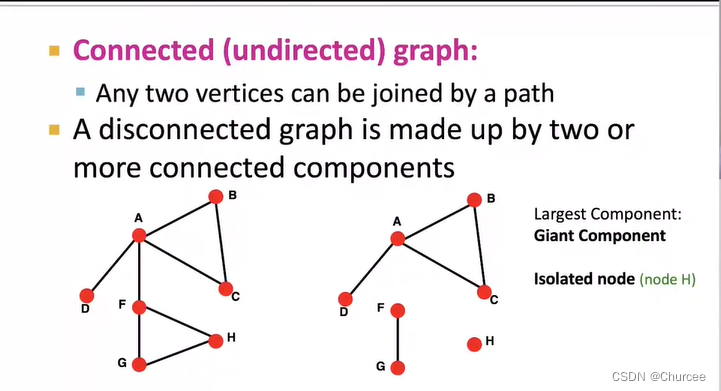
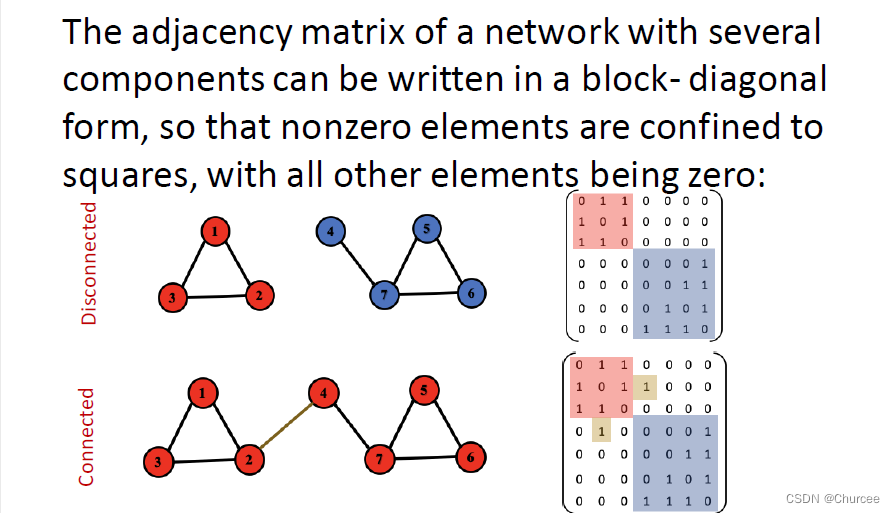
当图没有连通时,邻接矩阵可以被分成几个对角块,所以在聚类系数里面只要弄清有几个对角块就可以知道有几类。 - 有向图的连通性
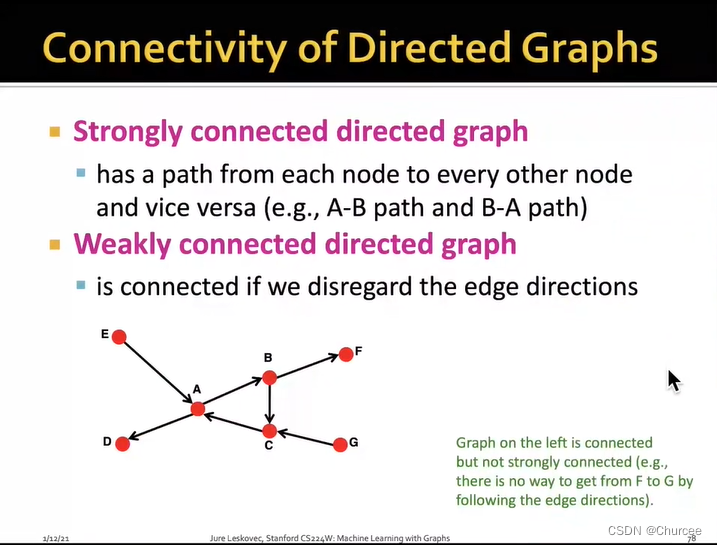
分为强连接和弱连接,强连接中的每对节点都相连,而弱连接则不是。
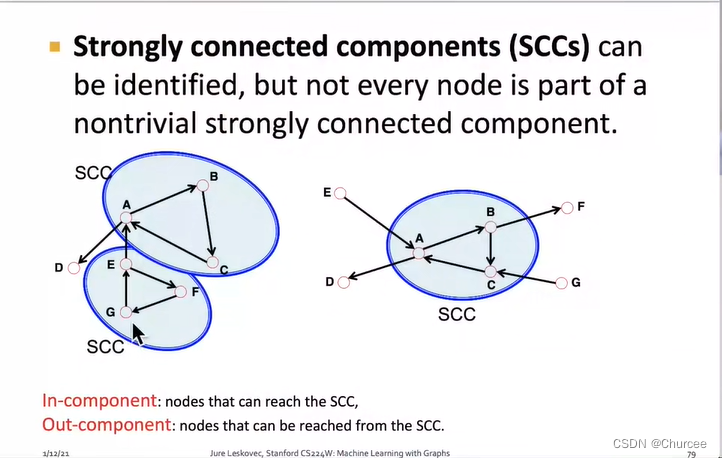
- 无向图的连通性