微积分与概率论基础

标签：cos 临边 lim 微积分 基础 对边 极限 概率论 sin

1、两边夹定理

当 \(x \in U(x_0,r)\) 时，有\(g(x) \leq f(x) \leq h(x)\)成立，并且 $$\lim_{x \to x_0}g(x)=A , \lim_{x \to x_0}h(x)=A$$
那么

\[\lim_{x \to x_0}f(x)=A \]

（1）极限

三角函数边与角度的关系：

1. tanx = 对边 / 临边
2. sinx = 对边 / 斜边
3. cosx = 临边 / 斜边
4. cotx = 临边 / 对边

注意：由于弧长=圆心角*半径，因此弧\(\mathop{AB}\limits^{\frown}\)长度为x；另外线段OC的长度为cosx，BC线段长度为sinx；由于tanx=对边/临边，因此AD线段长度为tanx。

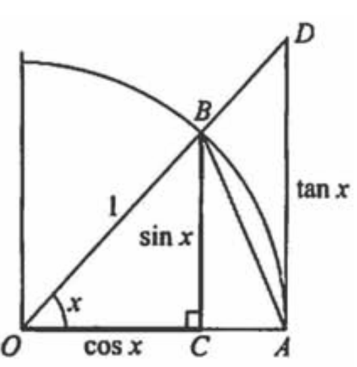
• 因此：sinx：\(\sin x<x<\tan x\)，\(x \in U(x_0, \varepsilon)\)
• 从而：\(1 < x/ \sin x < 1/ \cos x\)
• 即：\(\cos x < \sin x /x < 1\)
• 因为：$$\lim_{x \to 0} \cos x = \cos 0 = 1$$
• 从而：$$\lim_{x \to 0} \frac{\sin x}{x}=1$$
• 该式将三角函数和多项式建立了极限关系

（2）思考平方

同理上式的平方依然是1，即：

\[\lim_{x \to 0} \frac{\sin^2 x}{x^2} = 1 \]

2、极限存在定理

单调有界数列必有极限。
单调数列有上界，则其必有极限。

标签：cos,临边,lim,微积分,基础,对边,极限,概率论,sin
From： https://www.cnblogs.com/xiugeng/p/16928802.html