CF1650G 『Counting Shortcuts』题解

标签：Shortcuts 题解短路 int text CF1650G 转移 dp dis

从洛谷博客那里搬过来的（

~~图论专题本来打算先挑最简单的做，结果做了两个多小时（~~

题意就是让你找从起点 \(s\) 到终点 \(t\) 的最短路以及次短路个数，本题次短路长度指的是最短路长度 \(-1\)。

考虑 \(\text{DP}\)。

设 \(dp_{u,0/1}\) 为当前到了点 \(u\)，\(0/1\) 是与 \(s\) 到 \(u\) 的最短路长度相差 \(0/1\) 的路径的条数。

手模几组样例容易得出转移方程。先跑一遍 \(\text{Dijkstra}\) 算出 \(s\) 到所有点的最短路 \(dis\)，设当前点为 \(u\)，下一个点为 \(v\)。则有：

若 \(dis_u = dis_v\)，则说明 \(v\) 的最短路并非 \(u\) 的最短路 \(+1\)，而是 \(u\) 的最短路和 \(v\) 的最短路差 \(1\)，则可 \(dp_{u, 0} \to dp_{v, 1}\)。
若 \(dis_u = dis_v\)，则说明 \(v\) 的最短路是可以由 \(u\) 转移过来的。于是v继承u的所有状态。即：\(dp_{u, 0} \to dp_{v, 0}\text{，}dp_{u, 1} \to dp_{v, 1}\)。

初态是 \(dp_{s, 0} = 1\)，因为题目问的是最短路与次短路个数之和所以末态为 \(dp_{t, 0} + dp_{t, 1}\)。

至此就可以高高兴兴写出一个 \(\text{dfs}\) 代码了。

void dfs(int x) {
	if (x == hd)
		return ;
	vis[x] = true;
	for (re i = head[x] ; i ; i = e[i].nxt) {
		int v = e[i].v;
		if (vis[v] == true)
			continue;
		if (dis[v] == dis[x])
			Plus(dp[v][1], dp[x][0]);
		else if (dis[v] == dis[x] + 1)
			Plus(dp[v][0], dp[x][0]), Plus(dp[v][1], dp[x][1]);
		dfs(v);
	}
	vis[x] = false;
}

然后测一下前三个样例，哇，都过了。以为这题就要切了，测第四个样例结果发现输出 1204。

显然是转移多了。考虑下面一张图：

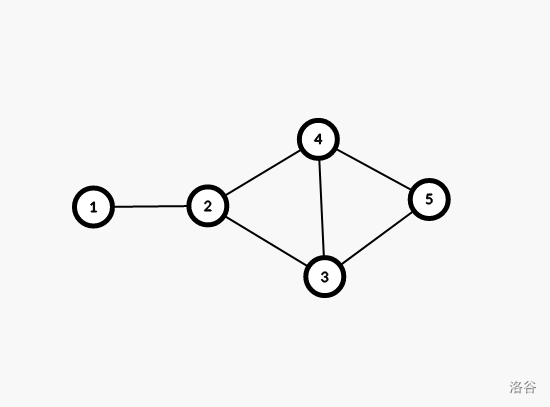
按照写的 \(\text{dfs}\) 模一下发现点 \(4\) 和点 \(3\) 转移到点 \(5\) 的时候出现了问题：转移顺序。

比如转移顺序：\(2 \to 4 \to 5\)，但是还有 \(2 \to 3 \to 4 \to 5\)，发现在第一遍转移的时候已经转移给了点 \(5\)，但是第二次转移的时候除了把新的值转移给了 \(5\)，还把以前的值又转移了一遍。所以就转移多了。

考虑如何解决。既然你是重复转移了前一次的，那我对于每个点转移过了之后把他的 \(\text{dp}\) 值清空，下一次再来到这个点的时候就不会重复转移上一次的值了。

void dfs(int x) {
	if (x == hd)
		return ;
	vis[x] = true;
	for (re i = head[x] ; i ; i = e[i].nxt) {
		int v = e[i].v;
		if (vis[v] == true)
			continue;
		if (dis[v] == dis[x])
			Plus(dp[v][1], dp[x][0]);
		else if (dis[v] == dis[x] + 1)
			Plus(dp[v][0], dp[x][0]), Plus(dp[v][1], dp[x][1]);
		dfs(v);
	}
	dp[x][0] = dp[x][1] = 0;// 多加了这一句
	vis[x] = false;
}

交上去会发现 TLE on test #3，我不太清楚 \(\text{dfs}\) 常数大还是咋地，卡了半天常也过不去（

考虑换一种解决方法。发现重复转移的实质就是拿还没转移完毕的去更新其他的了，于是考虑如何让他转移完毕再去更新。

注意到点 \(u\) 所有的转移都是对于 \(dis_v = dis_u\) 或 \(dis_v = dis_u + 1\) 的 \(v\) 去转移，这启示我们按照 \(dis\) 对原图进行分层。对于每个点 \(u\) 先对于同层也就是 \(dis_v = dis_u\) 的点 \(v\) 进行转移，全部转移完毕后再去转移 \(dis_v = dis_u + 1\) 的点 \(v\) 即可。

#pragma GCC optimize(2)
#include <iostream>
#include <cstdio>
#include <queue>
#include <vector>
#define GMY (520 & 1314)
#define char_phi int
#define re register int
#define FBI_OPENTHEDOOR(x, y) freopen(#x ".in", "r", stdin), freopen(#y ".out", "w", stdout)
#define N 2000005
#define M 2000005
#define P 1000000007
using namespace std;
inline void Fastio_setup() { ios :: sync_with_stdio(false); cin.tie(NULL), cout.tie(NULL); }
inline int MAX(int x, int y) { return ((x > y) ? (x) : (y)); }
inline int MIN(int x, int y) { return ((x < y) ? (x) : (y)); }
 
int n, m, star_cnt, yd, hd;
char vis[N];
int head[N], q[M<<3], dis[N];
int dp[N][2];
 
struct star { int v, nxt; };
struct Node {
	int x, d;
	
	friend bool operator < (Node A, Node B) { return A.d > B.d; }
};
 
struct star e[M<<1];
 
priority_queue<Node> heap;
vector<int> vec[N];
 
inline void star_add(int u, int v) { e[++ star_cnt].v=v, e[star_cnt].nxt=head[u], head[u]=star_cnt; }
inline void Clean() {
	star_cnt = 0; vec[0].clear();
	for (re i = 1 ; i <= n ; ++ i) {
		head[i] = dp[i][0] = dp[i][1] = 0;
		vec[i].clear();
	}
}
 
inline void Dijkstra() {
	int x = yd; for (re i = 1 ; i <= n ; ++ i) dis[i] = 0x3f3f3f3f, vis[i] = false;
	heap.push( (Node) {x, 0} ); dis[x] = 0;
	while (heap.empty() == false) {
		x = heap.top().x; heap.pop();
		if (vis[x] == true)
			continue;
		vis[x] = true;
		for (re i = head[x] ; i ; i = e[i].nxt) {
			int v = e[i].v;
			if (dis[v] > dis[x] + 1) {
				dis[v] = dis[x] + 1;
				if (vis[v] == false)
					heap.push( (Node) { v, dis[v] } );
			}
		}
	}
}
inline void Plus(int& who, int val) { who += val; if (who >= P) who -= P; }
 
inline void Search() {// 先更新0再更新1
	for (re i = 1 ; i <= n ; ++ i) {
		vis[i] = false;
		vec[dis[i]].emplace_back(i);
	}
	
	dp[yd][0] = 1;
	for (re dep = 0 ; dep <= n ; ++ dep) {
		for (auto x : vec[dep])
			for (re i = head[x] ; i ; i = e[i].nxt) {// 先转移同层的
				int v = e[i].v;
				if (dis[v] == dep)
					Plus(dp[v][1], dp[x][0]);
			}
		for (auto x : vec[dep])
			for (re i = head[x] ; i ; i = e[i].nxt) {// 再转移其他层的
				int v = e[i].v;
				if (dis[v] == dep + 1)
					Plus(dp[v][0], dp[x][0]), Plus(dp[v][1], dp[x][1]);
			}
	}
}


inline void work() {
	Clean();
	cin >> n >> m; cin >> yd >> hd;
	for (re i = 1, uu, vv ; i <= m ; ++ i)
		{cin >> uu >> vv; star_add(uu, vv), star_add(vv, uu);}
	
	Dijkstra();
	Search();// 也许算是bfs罢
	
	cout << (dp[hd][0] + dp[hd][1]) % P << '\n';
}
 
#undef int
// #define IXINGMY
char_phi main() {
	#ifdef IXINGMY
		FBI_OPENTHEDOOR(a, a);
	#endif
	Fastio_setup();
	int T; cin >> T;
	while (T --)
		work();
	return GMY;
}

\(\text{Hint}\)：参考了 \(\text{Jerry-Black}\) 大佬的思路。

标签：Shortcuts,题解,短路,int,text,CF1650G,转移,dp,dis
From： https://www.cnblogs.com/charphi/p/16888352.html

CF1650G 『Counting Shortcuts』题解

相关文章

赞助商

阅读排行

CF1650G 『Counting Shortcuts』 题解

相关文章

赞助商

阅读排行

CF1650G 『Counting Shortcuts』题解