前言
本文将基于各大优质博客题解并加之个人的总结,主要内容包括四类背包问题:0-1背包问题,完全背包问题,多重背包问题和分组背包问题。
0-1背包问题
题目
题解代码
1. 二维版本
状态\(f[i][j]\)定义:前 \(i\) 个物品(包括 \(i\) ),背包容量 \(j\) 下的最优解(最大价值)
根据在背包容量为 \(j\) 的情况下是否选取物品 \(i\) ,可以求得状态转移方程为:
\[f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i]) \]含义:
(1) 如果不装第 \(i\) 件物品,那么问题就转化为“前 \(i-1\) 件物品放入容量为 \(j\) 的背包中的最大价值”
(2) 如果装第 \(i\) 件物品,那么问题就转化为“前 \(i-1\) 件物品放入剩下的容量为 \(j-v[i]\) 的背包中的最 大价值”
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
f[i][j] = f[i - 1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
}
cout << f[n][m];
return 0;
}
2. 一维版本
观察原来的状态转移方程由于原来的\(f[i][j]\)都是由它左上角的状态更新过来的,并且仅由\(f[i-1]\)这一层状态更新,所以我们可以采用滚动数组的形式,也就是相当于总共就两行状态,第二行状态由第一行状态更新,第一行状态又由第二行状态更新,如此循环。最后,我们可以将二维数组压缩成一维数组。
我们将原来状态转移方程第一维抹除(但是你脑子里得当做它存在),此时的状态转换方程为:
\[f[j] = max(f[j], f[j - v[i]] + w[i]) \]此时 \(f[j]\) 的含义:背包容量 \(j\) 下的最优解(最大价值)
此时我们得关注遍历顺序,\(i\) 在外层,\(j\) 在内层,并且 \(j\) 需要逆序遍历!具体原因可以看这篇题解01背包问题 一维动态规划状态转移方程的解释
此时我们可以采取第一步优化(此处可参考题解01背包问题(状态转移方程讲解))
for(int i = 1; i <= n; i++)
for(int j = m; j >= 0; j--)
{
if(j < v[i])
f[i][j] = f[i - 1][j]; // 优化前
f[j] = f[j]; // 优化后,该行自动成立,可省略。
else
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]); // 优化前
f[j] = max(f[j], f[j - v[i]] + w[i]); // 优化后
}
实际上,只有当枚举的背包容量 \(>=v[i]\) 时才会更新状态,因此我们可以修改循环终止条件进一步优化。
for(int i = 1; i <= n; i++)
{
for(int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
最终我们可以得到一维版本的代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
完全背包问题
题目
题解代码
1. 二维版本
状态 \(f[i][j]\) 的定义与0-1背包是一样的,都是指:前\(i\)个物品(包括 \(i\) ),背包容量 \(j\) 下的最优解(最大价值)
首先画出y氏思考流程图: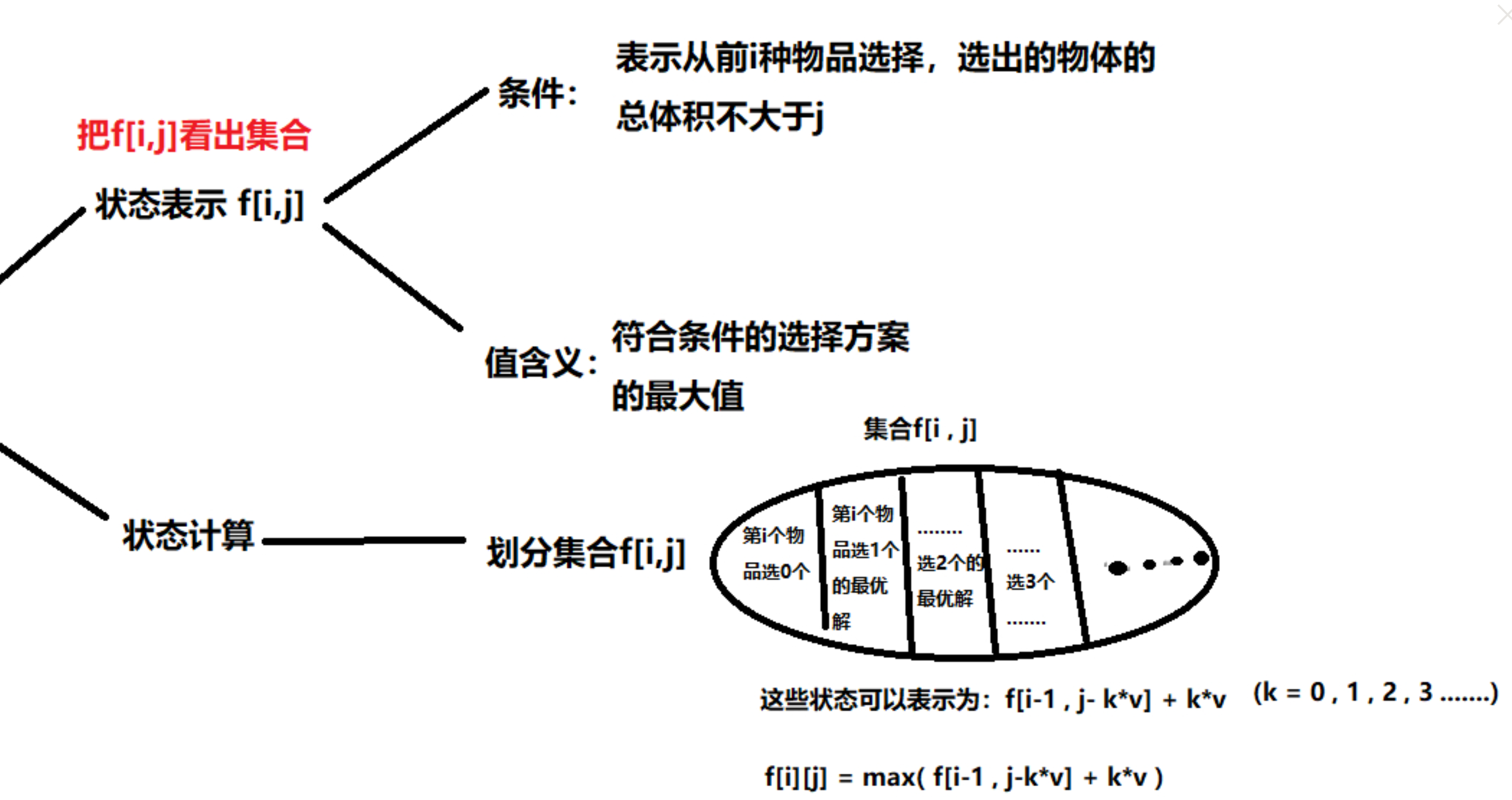
画出这张图之后,就可以比较容易写出以下代码了:
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
for(int k = 0; k <= j / v[i]; k++)
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
cout << f[n][m];
return 0;
}
2. 一维版本
以下部分主要取自Charles__的题解,很感谢他的题解,让我弄懂了优化的思路~
我们考虑以下两个式子的递推方程:
\[f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w , f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....) \]\[f[i , j-v]= max( f[i-1,j-v] , f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , .....) \]以上两个式子我们可以对比发现\(f[i][j - v]\)就是\(f[i][j]\)中除了第一项以外的项\(+w\),那么我们就可以将最终的状态转移方程简化为:
\[f[i][j]=max(f[i-1][j], f[i,j-v]+w) \]于是我们便可以对代码进行修改,我们首先可以去掉最内层的for循环:
for(int i = 1; i <= n; i++)
{
for(int j = 0; j <= m; j ++)
{
f[i][j] = f[i - 1][j];
if(j - v[i] >= 0)
f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
}
到了这一步,其实跟0-1背包已经很像了,直接去掉一维,得到以下代码:
for(int i = 1; i <= n; i++)
for(int j = v[i]; j <= m; j++) // 注意这里必须是正序遍历!
f[j] = max(f[j], f[j - v[i]] + w[i]);
对于遍历顺序的解释说明:
我们发现这里的第二层循环和0-1背包是相反的,可以这样来理解,首先来看一下两者最终的状态转换方程:
0-1背包:
\[f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i]) \]完全背包:
\[f[i][j]=max(f[i-1][j], f[i,j-v]+w) \]只有一个区别,注意两者第二个下标,由于是采用滚动数组的形式优化,完全背包是\(i\),说明用到的是当层已经完成更新的先前状态去更新当层正在更新的状态,而0-1背包是\(i-1\),说明是上层的状态去更新当层的状态,所以说完全背包需要的是正序,而0-1是逆序!
最终得到一维版本完整代码:
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = v[i]; j <= m; j++)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m];
return 0;
}