posted on 2021-10-23 22:52:47 | under 题解 | source
分类讨论。
一句话题意:求 \(\max\limits_{i=l}^{r}\{i\bmod n\}\)
首先画个数轴,按除以 \(n\) 向下取整的商把这些整数分块,大概是这样:
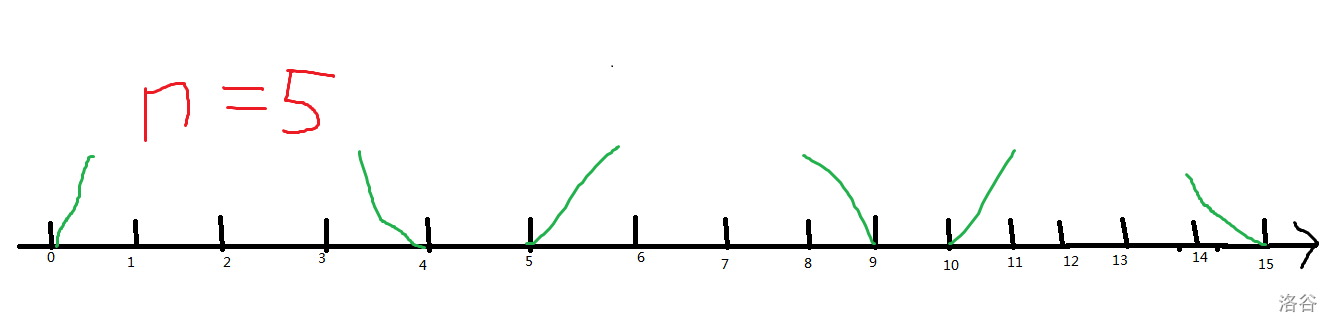
容易看出每块中的整数 \(\bmod n\) 的值单调递增,越往右越大。
接着,如果 \(l\) 和 \(r\) 不在同一块:
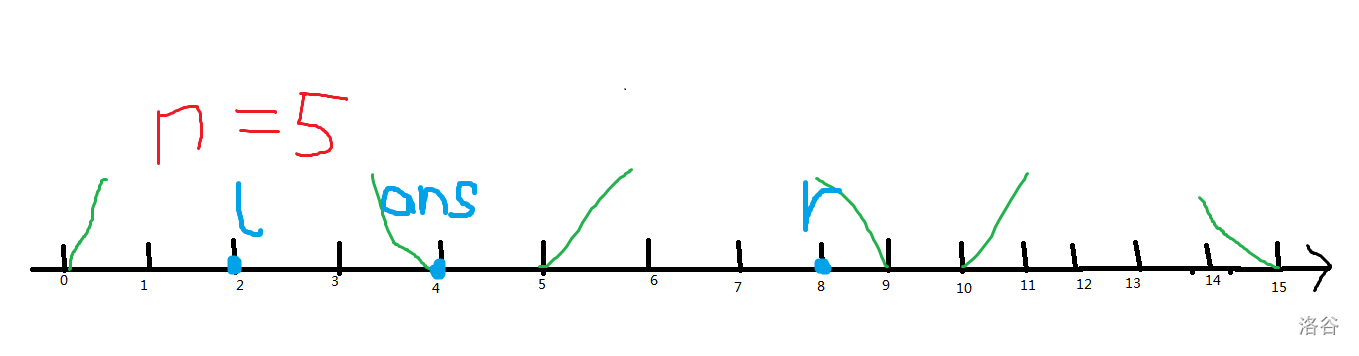
那么 \(l\) 和 \(r\) 一定会跨过一个块的右端点,所以 \(ans=n-1\)。
如果 \(l\) 和 \(r\) 在同一块:
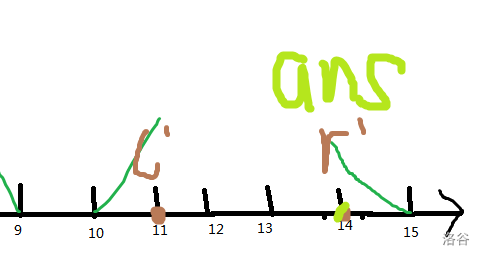
那 \(ans\) 最多能取到 \(r\bmod n\)。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
LL n,l,r;//其实不开 LL 也行
int main(){
freopen("candy.in","r",stdin);
freopen("candy.out","w",stdout);
scanf("%lld%lld%lld",&n,&l,&r);
if(l/n!=r/n) printf("%lld\n",n-1);
else printf("%lld\n",r%n);
return 0;
}