洛谷 [AGC021B] Holes 蓝 题解

标签：10 洛谷 int 题解 top Holes stk poi PDD

前言

学校基础模拟赛的题，当时有思路但是不太会写凸包就没做，下来看了看，自己的思路大部分是正确的，有些细节没有想到，在此写篇题解。

我用的是 Andrew 求凸包。

思路

答案为 0 的点

题目说：坐标系半径 \(R=10^{10^{10^{10}}}\)，你可以感受一下这个数字的大小，这个数字比 \(10^6\) 要大得多得多！根本不在一个数量级上！如果我们把题目中的所有点的凸包求出来，那么随机出来的点在这个凸包里面的概率非常非常小，小到在精确度 \(10^{-5}\) 的要求上可以忽略。

这样就可以得到很重要的一个结论：对于不在凸包上的所有点，它们的答案为 0

凸包上的点

考虑凸包上的点的答案怎么求。到点的距离这个东西，初中数学书上有一条重要的定理：一个线段的中垂线到这个线段的两个端点的距离相等。那对于一个点，如何求凸包上的那个点离它最近呢？不太好求，换一种思路，能不能求出：对于凸包上的每个点 \(A_i\)，求出与之对应的极大的一个区域，使得这个区域上的所有点离点 \(A_i\) 的距离是最近的，且不在这个区域上的所有点离点 \(A_i\) 的距离不是最近的。先上图：

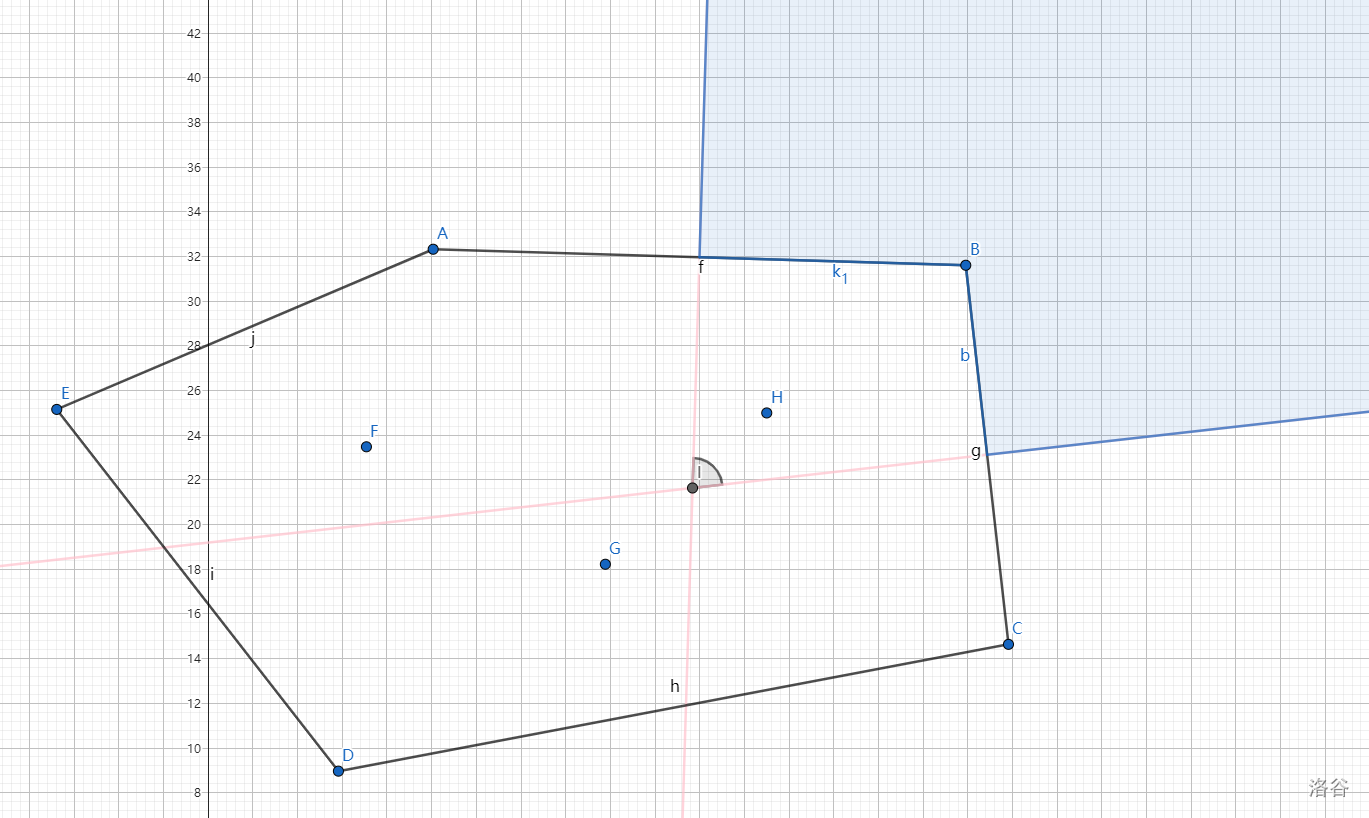
两条粉色的线分别为线段 \(AB,BC\) 的中垂线，那么能够直观感受到蓝色框框就是所求的极大的区域，这个区域里的所有点离点 \(B\) 是最近的。至于为什么不加凸包里面的部分，其实加和不加都一样，这么一点点面积，怎么能够和我 \(R=10^{10^{10^{10}}}\) 的坐标系相比较呢？根本不会影响答案。

那么点 \(B\) 的答案是多少呢？比较显然，就是两个中垂线所成夹角再除以 \(360^\circ\)，中垂线夹角也就是图中灰色的角。

怎么方便地求角度

你直接硬算肯定没问题，但是又更简单的方法，还拿上图举例子，如果我们能求出 \(\angle ABC\) 的大小，那么所求的灰色角的角度就是 \(180^\circ - \angle ABC\)，那么考虑如何求 \(\angle ABC\)

高中数学书上有一条重要的定理“余弦定理”：在 \(\triangle ABC\)，\(\cos C = \dfrac{a^2+b^2-c^2}{2ab}\)，其中线段 \(a,b,c\) 分别为角 \(A,B,C\) 对着的边，即：\(a=BC,b=AC,c=AB\)。

那么要求出 \(\angle ABC\)，我们可以先求出 \(\cos \angle ABC\)，再用反三角函数即可求出 \(\angle ABC\)

在这个图中 \(\cos \angle ABC = \dfrac{AB^2+BC^2-AC^2}{2 \cdot AB \cdot BC}\)，而点 \(A,B,C\) 的坐标都是已知的，那么很容易就能求出来，不赘述了。

细节问题

首先考虑如果一些点共线了该怎么办？如下图：

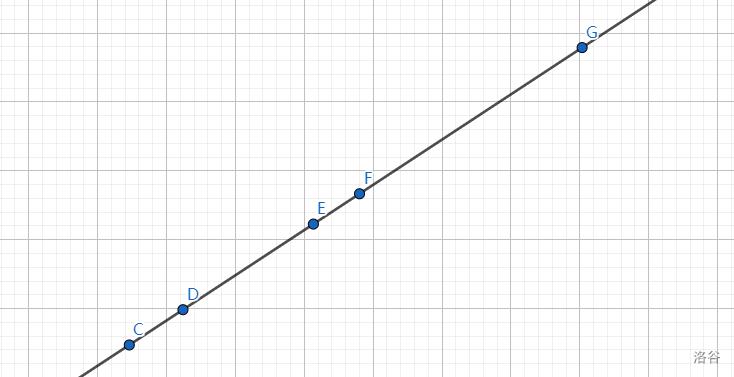
你还是每两个相邻点作中垂线，然后划分区域，得到下图：

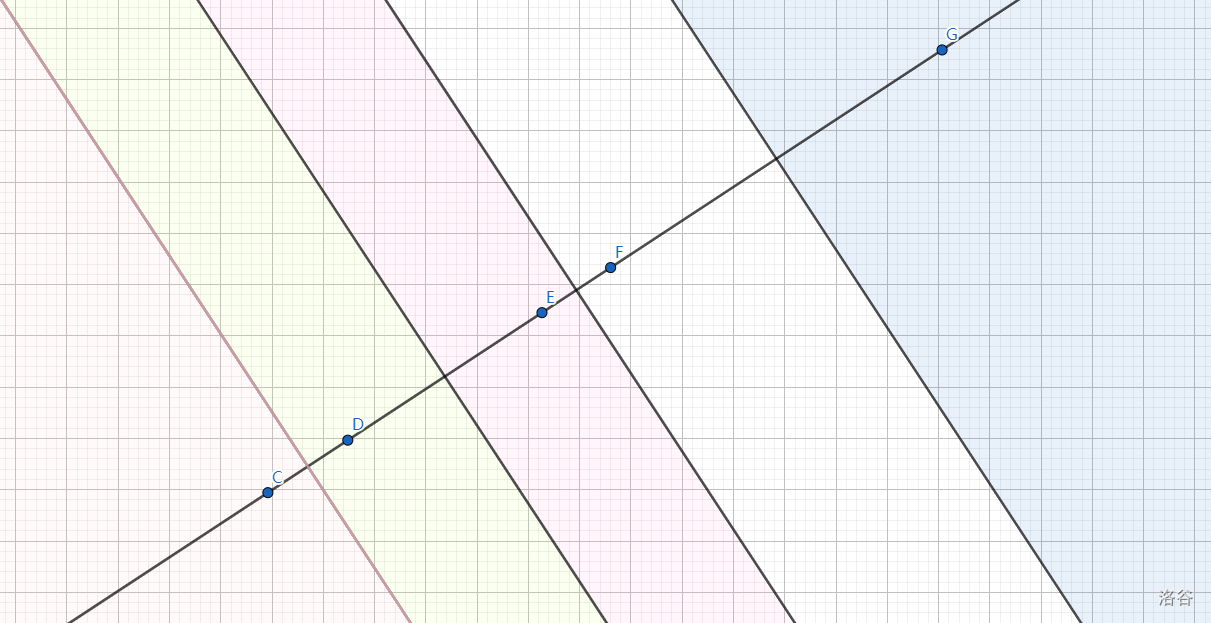
不用我多说，聪明的你一定能够知道每个区域是对应哪个点的，那么你考虑 \(C,D,E,F,G\) 这个五个点的答案分别是多少，答案：除了最左边的点 \(C\) 和最右边的点 \(G\) 的答案为 \(0.5\)，其他点的答案均为 \(0\)

为什么？虽然说 \(D,E,F\) 这三个点的区域也是无限向外延申的，但是他们可以形象地理解为“一维延伸”，确实，与直线垂直的方向上是无限延伸的，但是直线方向的长度是固定的；而对于 \(C,D\) 两点，他们可以形象地理解为“二维延伸”，与直线垂直的方向上是无限延伸的，直线方向上也是无限延伸的。还是那句话：“一维延伸”的区域怎么能够和我 \(R=10^{10^{10^{10}}}\) 的坐标系相比较呢？根本不会影响答案！

这说明求凸包时，要把共线的点当作不在凸包上，否则答案会错。

还有就是，如果只有一个点，那么直接输出 1 即可，这个很好理解。

Code

#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#define x first
#define y second

using namespace std;

typedef pair<double, double> PDD;
const int N = 210;
const double pi = acos(-1), pi_2 = 2 * acos(-1);

int n;
int top, stk[N];
struct warma
{
    PDD q;
    int id;
} poi[N];
double ans[N];

bool cmp(warma a, warma b)
{
    return a.q < b.q;
}

double get_dist(PDD a, PDD b)
{
    double dx = a.x - b.x;
    double dy = a.y - b.y;
    return sqrt(dx * dx + dy * dy);
}

double cross(PDD a, PDD b)
{
    return a.x * b.y - a.y * b.x;
}

double area(PDD a, PDD b, PDD c)
{
    PDD ab = (PDD){b.x - a.x, b.y - a.y};
    PDD ac = (PDD){c.x - a.x, c.y - a.y};
    return cross(ab, ac);
}

void andrew()
{
    sort(poi + 1, poi + 1 + n, cmp);
    top = 0;
    for (int i = 1; i <= n; i ++ )
    {
        while (top >= 2 && area(poi[stk[top - 1]].q, poi[stk[top]].q, poi[i].q) < 0) top -- ;
        stk[ ++ top] = i;
    }
    for (int i = n - 1; i >= 1; i -- )
    {
        while (top >= 2 && area(poi[stk[top - 1]].q, poi[stk[top]].q, poi[i].q) < 0) top -- ;
        stk[ ++ top] = i;
    }
    top -- ;
    stk[0] = stk[top], stk[top + 1] = stk[1]; //这么做为了防止越界，把它变成一个“环”
    return;
}


int main()
{
    // freopen("in.txt", "r", stdin);
    // freopen("out.txt", "w", stdout);
    cin >> n;
    if (n == 1)
    {
        printf("1\n");
        return 0;
    }
    for (int i = 1; i <= n; i ++ ) cin >> poi[i].q.x >> poi[i].q.y, poi[i].id = i;
    andrew();
    //以上是求凸包
    for (int i = 1; i <= top; i ++ )
    {
        double a = get_dist(poi[stk[i - 1]].q, poi[stk[i]].q);
        double b = get_dist(poi[stk[i]].q, poi[stk[i + 1]].q);
        double c = get_dist(poi[stk[i - 1]].q, poi[stk[i + 1]].q);
        double angle = pi - acos((a * a + b * b - c * c) / (2 * a * b)); //余弦定理
        ans[poi[stk[i]].id] = angle / pi_2;
    }
    for (int i = 1; i <= n; i ++ ) printf("%.10lf\n", ans[i]);
    return 0;
}

尾声

细节真是太多了，写这篇题解花了大概俩小时吧，还是有一些收获！还有 16 天左右就要 NOIP 了，准备退役啦！完结撒花！

标签：10,洛谷,int,题解,top,Holes,stk,poi,PDD
From： https://www.cnblogs.com/LittleMoMol-kawayi/p/solution_LuoGu_AT_agc021_b.html