首页 > 编程语言 >【算法】李超线段树

【算法】李超线段树

时间：2024-10-19 15:34:30浏览次数：7  
标签：return int 线段 李超 mid 算法 id cmp

1. 算法简介

李超线段树是用来维护一次函数的线段树，可以支持插入线段（一次函数），查询直线 \(x=k\) 的与区间内线段交点纵坐标的最值等操作。

考虑如何使用线段树维护线段。

可以利用标记永久化的思想，对于线段树内每一个节点存储所有在当前区间 \([l,r]\) 中，\(f(mid)\) 最大/最小的一次函数。

2. 算法实现

2.1 函数值比较函数

对于实数运算而言，运算的结果可能会丢失精度，这时我们需要定义一个比较函数 cmp 和误差精度常量 eps\(=10^{-9}\)。当两实数 \(x, y\) 比大小时，若 \(x-y>eps\) 则可判定为 \(x > y\)，其他比较同理。所有实数的存储最好使用 long double 来避免误差过大。

long double K(node x) {//斜率
  return 1.0 * (x.y1 - x.y0) / (x.x1 - x.x0);
}

long double B(node x) {//截距
  return 1.0 * x.y1 - K(x) * x.x1;
}

long double F(node t, long double x) {//f(x)值
  return t.k * x + t.b;
}

int cmp(long double x, long double y) {//比较函数
  if(x - y > eps) return 1;
  if(y - x > eps) return 0;
  if(fabs(x - y) <= eps) return -1;
}

2.2 插入线段

以维护最大值为例。

假设需要在李超线段树中插入线段 \(l_{new}:((x_1,y_1),(x_2,y_2))\)。首先从根节点走到线段树中修改的节点，即 \([x_1,l_1],[l_1+1,l_2],[l_2+1,l_3],\dots,[l_n,x2]\)。然后在每个区间插入线段。

具体而言，插入一条 \(l_{new}\) 步骤如下：

图示 1

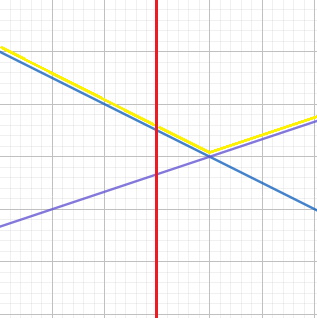
  1. 如果在当前 \(mid\) 处的 \(f_{new}(mid)>f_{old}(mid)\)，则将旧线段替换新线段；
  2. 如果在步骤 1 中未能替换成功：
    1. 如果 \(f_{new}(l)>f_{old}(l)\) 则说明 \(l_{new}\) 和 \(l_{old}\) 的交点在左侧，说明 \(l_{new}\) 能在 \([l,mid]\) 左儿子内还能产生贡献，递归处理左儿子；
    2. 如果 \(f_{new}(l)<f_{old}(l)\) 则说明 \(l_{new}\) 在左侧已经毫无贡献的可能，停止向儿子插入线段；
    3. 如果 \(f_{new}(r)>f_{old}(r)\) 则说明 \(l_{new}\) 和 \(l_{old}\) 的交点在右侧，说明 \(l_{new}\) 能在 \([mid+1,r]\) 右儿子内还能产生贡献，递归处理右儿子；
    4. 如果 \(f_{new}(r)<f_{old}(r)\) 则说明 \(l_{new}\) 在右侧已经毫无贡献的可能，停止向儿子插入线段；
  3. 如果在步骤 1 中替换成功：
    1. 如果 \(f_{old}(l)>f_{new}(l)\) 则说明 \(l_{old}\) 和 \(l_{new}\) 的交点在左侧，说明 \(l_{old}\) 能在 \([l,mid]\) 左儿子内还能产生贡献，递归处理左儿子；
    2. 如果 \(f_{old}(l)<f_{new}(l)\) 则说明 \(l_{old}\) 在左侧已经毫无贡献的可能，停止向儿子插入线段；
    3. 如果 \(f_{old}(r)>f_{new}(r)\) 则说明 \(l_{old}\) 和 \(l_{new}\) 的交点在右侧，说明 \(l_{old}\) 能在 \([mid+1,r]\) 右儿子内还能产生贡献，递归处理右儿子；
    4. 如果 \(f_{old}(r)<f_{new}(r)\) 则说明 \(l_{old}\) 在右侧已经毫无贡献的可能，停止向儿子插入线段；

Code：

void upd(int &p, int l, int r, int L, int R, int x) {//递归至修改节点
  if(!p) p = ++idx;
  if(L <= l && r <= R) {
    insert(p, l, r, x);
    return ;
  }
  int mid = l + r >> 1;
  if(L <= mid) upd(t[p].ls, l, mid, L, R, x);
  if(R > mid) upd(t[p].rs, mid + 1, r, L, R, x);
}

void insert(int &p, int l, int r, int x) {//插入线段
  if(!x) return ;
  if(!p) p = ++idx;
  int y = t[p].id, mid = l + r >> 1;
  if(x > y) swap(x, y);//模版题要求维护编号最小
  if(cmp(F(a[y], mid), F(a[x], mid)) == 1) swap(x, y);//将 f(mid) 大保存至该节点
  t[p].id = x;
  if(cmp(F(a[y], l), F(a[x], l)) == 1 || cmp(F(a[y], l), F(a[x], l)) == -1) {//左儿子有机会做贡献
    insert(t[p].ls, l, mid, y);
  }
  if(cmp(F(a[y], r), F(a[x], r)) == 1 || cmp(F(a[y], r), F(a[x], r)) == -1) {//右儿子有机会做贡献
    insert(t[p].rs, mid + 1, r, y);
  }
}

节点标记维护线段的编号即可，易实现且不占递归空间，比较函数大小时直接传入线段编号计算即可。

2.3 查询直线 \(x=k\) 与线段交点纵坐标最值

要做的跟单点查询一样，将线段树递归至单点的一路上的所有最值取最值即可。

其实就是每一个节点维护的是当前节点区间的 \(f(mid)\) 最值的线段，只要一路取最值那么便是直线 \(x=k\) 与所有已知线段交点的纵坐标最值了。

double ask(int p, int l, int r, int k) {
  if(l == r) return F(a[t[p].id], k);
  int mid = l + r >> 1;
  if(k <= mid) return max(F(a[t[p].id], k), ask(t[p].ls, l, mid, k));
  else return max(F(a[t[p].rs], k), ask(t[p].rs, mid + 1, r, k));
}

模版题要求查询纵坐标最小值的节点编号，若相同则编号小的为答案。也是同理：

int ask(int p, int l, int r, int k) {
  if(l == r) return t[p].id;
  int mid = l + r >> 1;
  int x = t[p].id, y;
  if(k <= mid) y = ask(t[p].ls, l, mid, k);
  else y = ask(t[p].rs, mid + 1, r, k);
  if(x > y) swap(x, y);//编号最小 
  if(cmp(F(a[y], k), F(a[x], k)) == 1) swap(x, y);
  return x; 
}

返回值类型因题而已。

考虑所有操作的时间复杂度，修改，插入线段，查询操作是 \(O(\log n)\) 的。所以带上总操作 \(m\) 的时间复杂度就是 \(O(m\log n)\)。

P4097 【模板】李超线段树 / [HEOI2013] Segment

模版题，三个操作拼一起就好了。

#include<bits/stdc++.h>
#define int long long
#define For(i,l,r) for(int i=l;i<=r;++i)
#define FOR(i,r,l) for(int i=r;i>=l;--i)
#define eps 1e-9
#define MOD 39989
#define mod 1000000007
#define inf 39989

using namespace std;

const int N = 1e5 + 10, M = 1e7 + 10;

struct node {
  int x0, y0, x1, y1;
  long double k, b;
  int id;
} a[N];

struct Node {
  int ls, rs, id;
} t[M];

int m, last, Id, idx, rt;

long double K(node x) {
  return 1.0 * (x.y1 - x.y0) / (x.x1 - x.x0);
}

long double B(node x) {
  return 1.0 * x.y1 - K(x) * x.x1;
}

long double F(node t, long double x) {
  return t.k * x + t.b;
}

int cmp(long double x, long double y) {
  if(x - y > eps) return 1;
  if(y - x > eps) return 0;
  if(fabs(x - y) <= eps) return -1;
}

int ask(int p, int l, int r, int k) {
  if(l == r) return t[p].id;
  int mid = l + r >> 1;
  int x = t[p].id, y;
  if(k <= mid) y = ask(t[p].ls, l, mid, k);
  else y = ask(t[p].rs, mid + 1, r, k);
  if(x > y) swap(x, y);//编号最小 
  if(cmp(F(a[y], k), F(a[x], k)) == 1) swap(x, y);
  return x; 
}

void insert(int &p, int l, int r, int x) {
  if(!x) return ;
  if(!p) p = ++idx;
  int y = t[p].id, mid = l + r >> 1;
  if(x > y) swap(x, y);//编号最小
  if(cmp(F(a[y], mid), F(a[x], mid)) == 1) swap(x, y);
  t[p].id = x;
  if(cmp(F(a[y], l), F(a[x], l)) == 1 || cmp(F(a[y], l), F(a[x], l)) == -1) {
    insert(t[p].ls, l, mid, y);
  }
  if(cmp(F(a[y], r), F(a[x], r)) == 1 || cmp(F(a[y], r), F(a[x], r)) == -1) {
    insert(t[p].rs, mid + 1, r, y);
  }
}

void upd(int &p, int l, int r, int L, int R, int x) {
  if(!p) p = ++idx;
  if(L <= l && r <= R) {
    insert(p, l, r, x);
    return ;
  }
  int mid = l + r >> 1;
  if(L <= mid) upd(t[p].ls, l, mid, L, R, x);
  if(R > mid) upd(t[p].rs, mid + 1, r, L, R, x);
}

signed main() {
  ios::sync_with_stdio(0);
  cin.tie(0), cout.tie(0);
  cin >> m;
  while(m--) {
    int op, x0, y0, x1, y1, k;
    cin >> op;
    if(op == 0) {
      cin >> k;
      k = (k + last - 1) % MOD + 1;
      last = ask(rt, 1, inf, k);
      cout << last << '\n';
    } else {
      cin >> x0 >> y0 >> x1 >> y1;
      x0 = (x0 + last - 1) % MOD + 1;
      x1 = (x1 + last - 1) % MOD + 1;
      y0 = (y0 + last - 1) % mod + 1;
      y1 = (y1 + last - 1) % mod + 1;
      if(x0 > x1) swap(x0, x1), swap(y0, y1);
      if(x0 == x1) a[++Id] = (node){x0, y0, x1, y1, 0, 1.0*max(y0, y1), Id};
      else a[++Id] = (node){x0, y0, x1, y1, K((node){x0, y0, x1, y1}), B((node){x0, y0, x1, y1}), Id};
      upd(rt, 1, inf, x0, x1, Id);
    }
  }
  return 0;
}

P4254 [JSOI2008] Blue Mary 开公司

将 \(P\) 当作斜率，\(S-P\) 当做截距。一次方案当做一次函数。实现函数插入，查询即可。

#include<bits/stdc++.h>
#define int long long
#define For(i,l,r) for(int i=l;i<=r;++i)
#define FOR(i,r,l) for(int i=r;i>=l;--i)
#define eps 1e-9
#define inf 6e9

using namespace std;

const int N = 1e5 + 10, M = 1e6 + 10;

struct Node {
  double k, b;
} a[N];

struct node {
  int ls, rs, id;
} t[M];

int m, id, idx, rt;

int cmp(double x, double y) {
  if(x - y > eps) return 1;
  if(y - x > eps) return -1;
  if(fabs(x - y) <= eps) return 0;
}

double F(Node t, int x) {
  return t.k * x + t.b;
}

void insert(int &p, int l, int r, int x) {
  if(!x) return ;
  if(!p) p = ++idx;
  int y = t[p].id, mid = l + r >> 1;
  if(cmp(F(a[y], mid), F(a[x], mid)) == 1) swap(x, y);
  t[p].id = x;
  if(cmp(F(a[y], l), F(a[x], l)) == 1 || cmp(F(a[y], l), F(a[x], l)) == 0) {
    insert(t[p].ls, l, mid, y);
  }
  if(cmp(F(a[y], r), F(a[x], r)) == 1 || cmp(F(a[y], r), F(a[x], r)) == 0) {
    insert(t[p].rs, mid + 1, r, y);
  }
} 

double ask(int p, int l, int r, int k) {
  if(l == r) return F(a[t[p].id], k);
  int mid = l + r >> 1;
  if(k <= mid) return max(F(a[t[p].id], k), ask(t[p].ls, l, mid, k));
  else return max(F(a[t[p].rs], k), ask(t[p].rs, mid + 1, r, k));
}

signed main() {
  ios::sync_with_stdio(0);
  cin.tie(nullptr), cout.tie(nullptr);
  cin >> m;
  while(m--) {
    string op;
    double s, p;
    int x;
    cin >> op;
    if(op == "Project") {
      cin >> s >> p;
      a[++id] = (Node){p, s-p};
      
      insert(rt, 1, inf, id); 
    } else {
      cin >> x;
      cout << floor(ask(rt, 1, inf, x) / 100)  << '\n';
    }
  }
  return 0;
}

3. 李超线段树斜率优化 dp

3.1 理论

假设有一个 dp 式子长成 \(dp_i=\min\limits_{1\le j < i}k_j x_i + b_j\) 的形式（或 \(\max\)，这里以 \(\min\) 为例），其中 \(k_j\) 可以为跟 \(j\) 有关的多项式，\(b_j\) 可以为跟 \(j\) 有关的多项式，\(x_i\) 可以为跟 \(i\) 有关的多项式。则可进行斜率优化 dp。

而使用李超线段树则可以无脑将斜优 dp 解决：先查询直线 \(x\) 与之前所有函数交点的纵坐标最值，更新 \(dp_i\)，再将 \(kx+b\) 插入李超线段树中。直到 dp 结束。

以 P2120 [ZJOI2007] 仓库建设 为例。

设 \(dp_i\) 表示前 \(i\) 个货物已经安置完毕，将部分货物安置在仓库 \(i\) 所需的最小代价。（距离记为 \(d\)，与题面 \(x\) 略有不同）

则可列出转移方程：

\[dp_i=\min\limits_{j\in[0,i-1]} \{dp_j + c_i + \sum\limits_{k\in[j+1,i]} p_k(d_i-d_k)\} \]

\[dp_i=\min\limits_{j\in[0,i-1]} \{dp_j + c_i + d_i\sum\limits_{k\in[j+1,i]} p_k - \sum\limits_{k\in[j+1,i]} p_kd_k\} \]

设 \(A_i=\sum\limits_{j=1}^ip_j\)，\(B_i=\sum\limits_{j=1}^i p_jd_j\)。

\[dp_i=\min\limits_{j\in[0,i-1]} \{dp_j + c_i + d_i(A_i-A_j) - B_i + B_j\} \]

\[dp_i=\min\limits_{j\in[0,i-1]} \{(-d_iA_j)+(dp_j+B_j)+(c_i-B_i+d_iA_i)\} \]

所以 \(k_j=-A_j,b_j=dp_j+B_j,x_i=d_i\) 然后再加上一坨 \((c_i-B_i+d_iA_i)\) 去更新 \(dp_i\)，再将 \(kx+b\) 插入李超线段树中。

及得 \(p_i=0\) 的细节：最后的一些地方没有货物可以不建厂。

#include<bits/stdc++.h>
#define int long long
#define eps 1e-9
#define For(i,l,r) for(int i=l;i<=r;++i)
#define FOR(i,r,l) for(int i=r;i>=l;--i)
#define inf 2147483648

using namespace std;

const int N = 1e6 + 10, M = 1e7 + 10;

struct Node {
  int ls, rs, id;
} t[M];

int n, d[N], p[N], A[N], B[N], c[N], dp[N], idx, rt, ans;

int cmp(int x, int y) {
  if(x - y > eps) return 1;
  if(y - x > eps) return -1;
  return 0;
}

int F(int id, int x) {
  return -A[id] * x + dp[id] + B[id];
}

void insert(int &p, int l, int r, int x) {
  if(!p) p = ++idx;
  int y = t[p].id, mid = l + r >> 1;
  if(cmp(F(x, mid), F(y, mid)) == 1) swap(x, y);
  t[p].id = x;
  if(cmp(F(x, l), F(y, l)) == 1) {
    insert(t[p].ls, l, mid, y);
  }
  if(cmp(F(x, r), F(y, r)) == 1) {
    insert(t[p].rs, mid + 1, r, y);
  }
}

int ask(int p, int l, int r, int k) {
  if(l == r) return F(t[p].id, k);
  int mid = l + r >> 1;
  if(k <= mid) return min(F(t[p].id, k), ask(t[p].ls, l, mid, k));
  else return min(F(t[p].id, k), ask(t[p].rs, mid + 1, r, k));
}

signed main() {
  ios::sync_with_stdio(0);
  cin.tie(nullptr), cout.tie(nullptr);
  cin >> n;
  For(i,1,n) cin >> d[i] >> p[i] >> c[i];
  For(i,1,n) {
    A[i] = A[i-1] + p[i];
    B[i] = B[i-1] + p[i] * d[i];
  }
  For(i,1,n) {
    dp[i] = ask(rt, 0, inf, d[i]) + (d[i] * A[i] - B[i] + c[i]);
    insert(rt, 0, inf, i);
  }
  ans = dp[n];
  FOR(i,n,1) {
    if(!p[i]) ans = min(ans, dp[i-1]);
    else break;
  }
  cout << ans << '\n';
  return 0;
}

标签：return,int,线段,李超,mid,算法,id,cmp
From： https://www.cnblogs.com/Daniel-yao/p/18475952

相关文章

  • 公共自行车借用量的分析与预测算法的实现
    个人名片......
  • 强化学习算法笔记之【DDPG算法】
    强化学习笔记之【DDPG算法】目录强化学习笔记之【DDPG算法】前言：原论文伪代码DDPG中的四个网络代码核心更新公式前言：本文为强化学习笔记第二篇，第一篇讲的是Q-learning和DQN就是因为DDPG引入了Actor-Critic模型，所以比DQN多了两个网络，网络名字功能变了一下，其它的就是软更新之......
  • acwing第二章算法模板
    17、单链表//head存储链表头，e[]存储节点的值，ne[]存储节点的next指针，idx表示当前用到了哪个节点inthead,e[N],ne[N],idx;//初始化voidinit(){    head=-1;    idx=0;}//在链表头插入一个数avoidinsert(inta){    e[idx]=a,ne[idx]=......
  • acwing第三章算法模板
    29、树与图的存储树是一种特殊的图，与图的存储方式相同。对于无向图中的边ab，存储两条有向边a->b,b->a。因此我们可以只考虑有向图的存储。(1)邻接矩阵：g[a][b]存储边a->b(2)邻接表：//对于每个点k，开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头结点int......
  • 【贪心算法】（第四篇）
    目录最⻓连续递增序列（easy）题目解析讲解算法原理编写代码买卖股票的最佳时机（easy）题目解析讲解算法原理编写代码最⻓连续递增序列（easy）题目解析1.题目链接：.-力扣（LeetCode）2.题目描述给定⼀个未经排序的整数数组，找到最⻓且连续递增的⼦序列，并返回该序列的⻓度。......
  • 【贪心算法】（第三篇）
    目录最⻓递增⼦序列（medium）题目解析讲解算法原理编写代码递增的三元⼦序列（medium）题目解析讲解算法原理编写代码最⻓递增⼦序列（medium）题目解析1.题目链接：https://leetcode.cn/problems/longest-increasing-subsequence/description/2.题目描述给你⼀个整数数组......
  • 贪心算法
    贪心算法基本要素1.贪心选择性质：通过每个子问题的最优选择，可以得到整个问题的最优解。意味着，当我们面对一个问题时，我们就可以通过贪心策略来做出局部最优的选择，最终得到全局最优的解。2.最优子结构：问题的最优解包含子问题的最优解。意味着，问题可以分解成若干个子问题，每个子问......
  • 贪心算法
    贪心算法基本要素1.贪心选择性质：通过每个子问题的最优选择，可以得到整个问题的最优解。意味着，当我们面对一个问题时，我们就可以通过贪心策略来做出局部最优的选择，最终得到全局最优的解。2.最优子结构：问题的最优解包含子问题的最优解。意味着，问题可以分解成若干个子问题，每个子问......
  • 贪心算法
    贪心算法 贪心算法基本要素1.贪心选择性质：通过每个子问题的最优选择，可以得到整个问题的最优解。意味着，当我们面对一个问题时，我们就可以通过贪心策略来做出局部最优的选择，最终得到全局最优的解。2.最优子结构：问题的最优解包含子问题的最优解。意味着，问题可以分解成若干个......
  • 数据结构与算法之线性表的基本操作
    数据结构之线性表的基本操作初始化，插入，获取#include<stdio.h>#include<stdlib.h>#include<malloc.h>#defineOK1#defineOVERFLOW-1#defineLIST_INIT_SIZE100#defineLISTINCREMENT10typedefintElemType;typedefstruct{ ElemType*elem; intlength; i......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99