1.1 枚举类问题
· 枚举是什么?
枚举也叫穷举,是计算机解决问题最基本的策略。其方法是一一列举所有的可能性,根据题意要求进行合理的判断或计算,最终得到答案,本质上就是一种搜索算法
基础的枚举就是人们常说的“暴力”求解。对于不同的问题,不可过分依赖“暴力”求解,应该根据具体的场景来进行具体分析,选择更加简洁和高效的算法。
枚举就是用for,while等循环来实现的,通常都一个一个的去试。如果试的数据符合已知条件,则就认为,这个数就是要的答案,就不再枚举下去了。所谓枚举,其实就是慢慢去试过去。但枚举有个坏处,若数据很大,很多,则枚举的范围就很广,又费空间,还费时间。所以用枚举的时候要想好空间范围,以确保达到时间的最简,与空间的最省。
枚举算法的运用场景就是适用于问题规模较小、解空间可穷举的情况。
\(思路很好想,代码很好写,只不过速度慢了一些。\)
· 总结一下:
- 运用循环把所有可能全试一遍,再根据题意做题。
- 枚举算法优点在于简单直观,不需要复杂的数学推导,易于实现。
- 缺点那就是运算量过大,当问题的规模变大的时候,循环的阶数越大,执行速度越慢,很容易超时。
1.2 枚举题目讲解
· P1149 [NOIP2008 提高组] 火柴棒等式
· 大意:
给你 \(n\) 根火柴棍,你可以拼出多少个形如 \(A+B=C\) 的等式?等式中的 \(A\)、\(B\)、\(C\) 是用火柴棍拼出的整数(若该数非零,则最高位不能是 \(0\))。用火柴棍拼数字 \(0\sim9\) 的拼法如图所示:
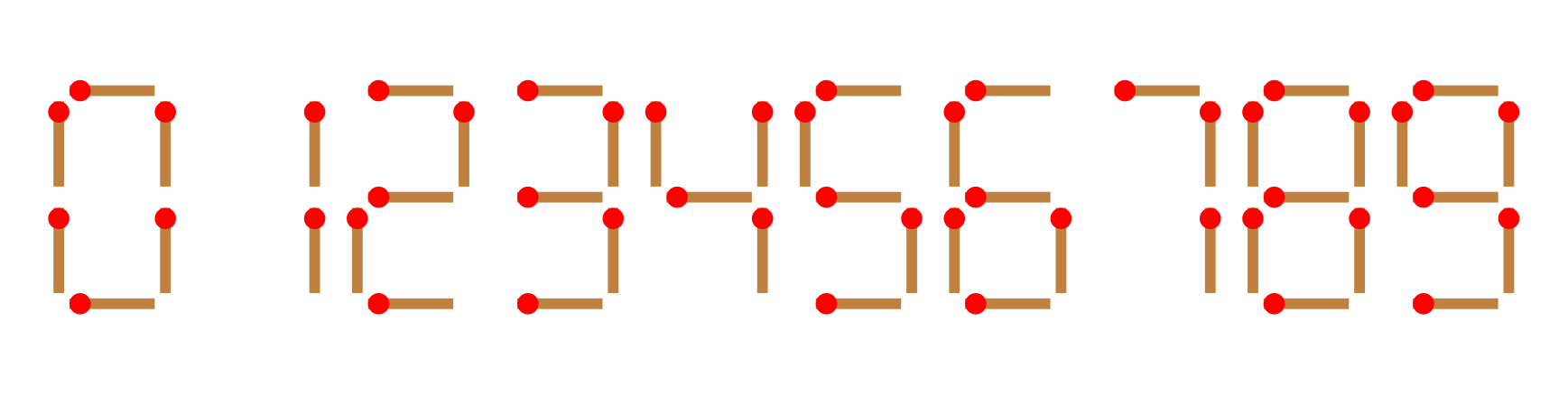
注意:
- 加号与等号各自需要两根火柴棍;
- 如果 \(A\neq B\),则 \(A+B=C\) 与 \(B+A=C\) 视为不同的等式(\(A,B,C\geq0\));
- \(n\) 根火柴棍必须全部用上。
样例 #1
样例输入 #1
14
样例输出 #1
2
· 讲解
我们可以先得到\(0-9\)各需要多少根火柴棒,然后再推出二位数,三位数,四位数各需要多少火柴棒。处理完后,我们可以直接枚举\(A\)和\(B\)。(可以证明\(A和B\)最大值为1111)、
\(Code:\)
点击我~ 获取代码
#include<bits/stdc++.h>
using namespace std;
int ans=0,n; //答案和火柴棒个数
int z[3005]={6,2,5,5,4,5,6,3,7,6}; //0~9所需的火柴棒
void f() //预处理出10~1111的所需火柴棒
{
for(int i=10;i<=2222;i++)
z[i]=z[i/10]+z[i%10]; //i/10为十位,i%10为个位
}
int main()
{
f(); //预处理每个数字应该需要的火柴棒根数
cin>>n;
for(int i=0;i<=1111;i++)
for(int j=0;j<=1111;j++)
{
int k=i+j; //k是A+B的和
if(z[i]+z[j]+z[k]+4==n) //加数+加数+和+等号与加号所需的火柴棒个数 为n的话,ans就++.
++ans;
}
cout<<ans<<'\n'; //输出
return 0;
}