算法总结-树链剖分

概念

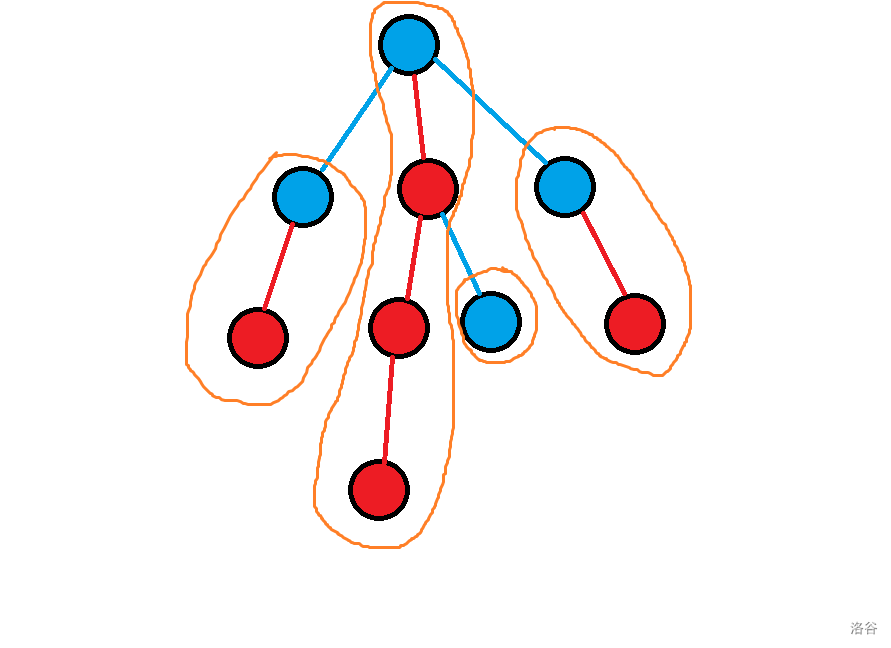
• 重儿子（红点）：父节点 \(f\) 的子节点中子树大小最大的儿子。

• 轻儿子（蓝点）：父节点 \(f\) 的子节点中除重儿子以外的节点。

• 重链（橙圈框出的链）：链顶为轻儿子，由重儿子组成的链。

  

重链剖分

用处：

1. 将树上任意一条路径划分成不超过 \(\log{n}\) 条连续的链（如实现求 \(LCA\)，优化时间复杂度等）。
2. 划分出每条链上节点的 \(DFS\) 序，使树上的节点成为一个连续的序列，便于维护树上的操作（如线段树，分块等）。

实现：

• 第一遍 \(DFS\)：

1. \(dep\) 数组：存储每个节点的深度。

2. \(father\) 数组：存储每个节点的父节点。

3. \(size\) 数组：存储每个节点的子树大小。

4. \(son\) 数组：存储每个节点的重儿子。

   void dfs1(int x,int f){
       dep[x]=dep[f]+1;
       fa[x]=f;
       sz[x]=1;
       for(int i=0;i<e[x].size();i++){
           int y=e[x][i];
           if(y==f) continue;
           dfs1(y,x);
           sz[x]+=sz[y];
           if(sz[son[x]]<sz[y]) son[x]=y;//更新重儿子
       }
       return ;
   }
   

• 第二遍 \(DFS\)：

  1. \(top\) 数组：记录每条重链的链顶。

  • 生成 \(dfs\) 序列（看情况是否需要）：

    1. \(dfn\) 数组：记录每个点搜到的顺序，也就是 \(dfs\) 序。
    2. 记录生成序列的数组。

  void dfs2(int x,int t){
  	top[x]=t;
      dfn[x]=++did;
      val[did]=a[x];//生成dfs序列（因题而异）
      if(!son[x]) return ;//没重儿子说明也没有轻儿子
      dfs2(son[x],t);
      for(int i=0;i<e[x].size();i++){
  		int y=e[x][i];
          if(y==fa[x]||y==son[x]) continue;
          dfs2(y,y);
      }
      return ;
  }
  

• 主函数：

  • 注：没有链的链顶为 \(0\) ,如果写成 \((1,0)\) ,则可能在某些情况下 \(TLE\)。

    int main(){
        ...
        dfs1(1,0);
        dfs2(1,1);//没有链的链顶为0,如果写成(1,0),则可能在有些情况下TLE
        ...
    }
  

运用

树链剖分求 \(LCA\)

• 思路：将深度更深的点跳到链顶的父节点，当两点跳到同一条链上时，此时深度更浅的一点必定为原先两点的 \(LCA\) 。

• 复杂度证明：因为已经被划分为 \(\log n\) 条链，所以最多只会有 \(log n\) 次跳到链顶的父节点，所以单次查询 \(LCA\) 的最坏时间复杂度为 \(O(\log n)\) 。

• 求 \(LCA\) 部分代码：

  void LCA(int x,int y){
  	while(top[x]!=top[y]){//链顶不同，说明不在同一条重链上
  		if(dep[top[x]]<dep[top[y]]) swap(x,y);
          x=fa[top[x]];
      }
      return dep[x]<dep[y]?x:y;//比较谁是LCA
  }
  

维护树上操作

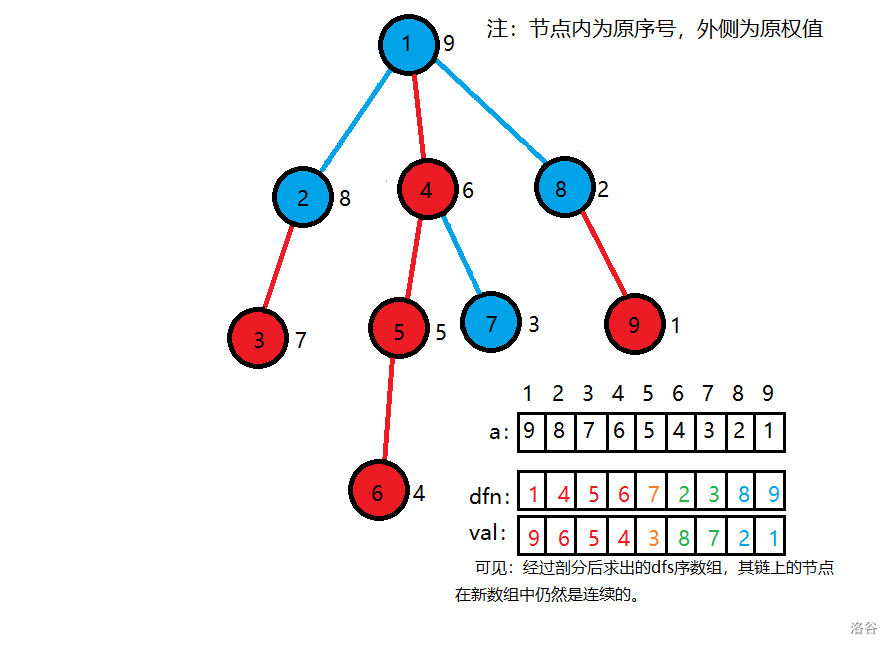
• 思路：将树上的点按照 \(dfs\) 序生成一个连续的序列，使用这个新的序列来进行修改等操作。建树等部分和原来大，修改、查询等操作需要找到其对应的区间。

  

• 具体见题目要求。

  • 模板：P3384 【模板】重链剖分/树链剖分。

  • 代码：

    • 生成新序列：

      void dfs2(int x,int t){
          top[x]=t;
          dfn[x]=++tid;
          val[tid]=a[x]%Mod;
          if(!son[x]) return ;
          dfs2(son[x],t);
          for(int i=0;i<e[x].size();i++){
              int y=e[x][i];
              if(y==fa[x]||y==son[x]) continue;
              dfs2(y,y);
          }
          return ;
      }
      

    • 建树。注：用新序列建树：

      void build(int k,int l,int r){
          if(l==r){
              sum[k]=val[l]%Mod;//注意这里用新序列建树
              return ;
          }
          int mid=(l+r)>>1;
          build(k<<1,l,mid);
          build(k<<1|1,mid+1,r);
          sum[k]=(sum[k<<1]+sum[k<<1|1])%Mod;
          return ;
      }
      

    • 新序列修改：

      void tree_modify(int x,int y,int v){
          while(top[x]!=top[y]){
              if(dep[top[x]]<dep[top[y]]) swap(x,y);//和求LCA一致
              modify(1,1,n,dfn[top[x]],dfn[x],v);//修改对应的新序列中的值
              x=fa[top[x]];
          }
          //当跳到同一条链上后还要进行一次,跳到同一节点。同一条链上的一段区间也要进行修改
          if(dep[x]<dep[y]) swap(x,y);
          modify(1,1,n,dfn[y],dfn[x],v);
          return ;
      }
      

    • 新序列查询：

      int tree_query(int x,int y){
          int ans=0;
          while(top[x]!=top[y]){
              if(dep[top[x]]<dep[top[y]]) swap(x,y);
              ans+=query(1,1,n,dfn[top[x]],dfn[x])%Mod;//同修改
              x=fa[top[x]];
          }
          //同修改
          if(dep[x]<dep[y]) swap(x,y);
          ans+=query(1,1,n,dfn[y],dfn[x])%Mod;
          return ans%Mod;
      }
      

    • 不懂的模拟一下样例：

      • 样例：

        /*#1
        5 5 2 24
        7 3 7 8 0 
        1 2
        1 5
        3 1
        4 1
        3 4 2
        3 2 2
        4 5
        1 5 1 3
        2 1 3
        */
        

      • 手摸：

        /*#1手玩 
         a :7 3 7 8  0
        dfn:2 1 5 3  4
        val:3 7 0 7  8
        //每行对应每次操作
        val:3 7 0 7 10
        val:5 9 2 9 12
        ans:2
        val:5 12 5 9 12
        ans:21
        */
        

To Be Continue