RT，主要介绍一些经典的分治算法

CDQ 分治

经典人类智慧算法。

三维偏序问题

三维偏序是 CDQ 分治的一个经典应用，搭配树状数组可以在 \(O(n\log^2n)\) 的时间复杂度内解决问题。如果我们枚举每一个元素，然后枚举其他的元素的话，可以在 \(O(n^2)\) 的时间复杂度解决这个问题，但显然无法满足需求。

我们可以先按照 \(a_i\) 排序，这样可以保证第 \(i\) 个元素前的所有元素均满足第一维限制。这样问题就转换为了二维偏序问题，如果此时再按 \(b_i\) 排序，就会打乱第一维的顺序，显然不可取，为此，我们引出 CDQ 分治的一个大致模板。

定义 \(\text{solve}(l,r)\) 为：求出所有 \(i\in [l,r]\) 的元素所受 \([l,r]\) 内其他元素的影响值。显然可以将 \(\text{solve}(l,r)\) 分为三部分（定义 \(mid=\frac{l+r}{2}\)）。

• \(\text{solve}(l,mid)\)

• \(\text{solve}(mid+1,r)\)

• 求解 \([l,mid]\) 内的元素对于 \([mid+1,r]\) 的元素的影响。

重复上述过程，递归边界是 \(l=r\)。

根据定义很好解释。我们发现可以下手优化的地方主要在第三部分，按照暴力做法，对于第三部分，我们枚举所有 \(i\in[mid+1,r]\) 内的元素，在 \([l,mid]\) 中查找，定义 \(m=r-l+1\)，时间复杂度 \(O(m^2)\)，有继续优化的空间。

我们发现，对于任何 \(i\in[l,mid],j\in[mid+1,r]\) 都始终满足 \(a_i\le a_j\)，因为序列最初是有序的，分治只在每一个区间内进行，所以不影响整体的单调性。所以说，即使将两个区间分别按照 \(b_i\) 的值升序排序，上述性质依然成立。

我们定义两个指针 \(i=l,j=mid+1\)，每当 \(j\to j+1\)，\(i\) 就不断移动直到第一次移动到 \(b_i>b_j\)，因为我们已经按照 \(b_i\) 的值升序排序，所以 \(i,j\) 的移动均是单调的，且每次两个指针移动后满足任何 \(k\in[l,i-1]\) 均满足 \(a_k\le a_j,b_k\le b_j\)。此时只差第三维限制。

我们思考平时解决二维偏序问题主要依靠排序和树状数组，利用树状数组限制第二维，而此时我们也可以在三维偏序中使用树状数组来限制第三维。具体做法，\(i\) 指针每移动一次，就将一个新的元素加入树状数组，在 \(c_i\) 的位置上加 \(1\)，每当查询时，就访问 \([0,c_j]\) 的和。这样我们就解决这个问题了。

时间复杂度：CDQ 分治 一般是子问题的时间复杂度乘上 \(O(\log n)\) ，就上面三维偏序问题来说，定义 \(m=r-l+1\)，排序为 \(O(m\log m)\)，指针扫描加树状数组为 \(O(m\log m)\)，所以最终时间复杂度为 \(O(n\log^2 n)\)。

同时，还存在几个小问题。

• CDQ 分治的一个特点是：在每次分治求解一个小区间时，不会涉及该区间外的部分，仅仅与当前小区间长度有关，所以在使用完树状数组后，不可以暴力清空，而应该还原原本的过程，以保证时间复杂度。

• 对于重复元素之间有贡献的，CDQ 分治无法直接解决，一个技巧是可以将元素离散化再求解。

• CDQ 分治的分治过程类似并归排序，所以在将序列按照 \(b_i\) 排序时，可以用并归排序替代。

贴出核心代码：

void merge(int l,int mid,int r){
    int i=l,j=mid+1,t=l;
    while(i<=mid||j<=r){
        if(j>r||(i<=mid&&cmp2(q[i],q[j])))book[t++]=q[i++];//cmp2指按b[i]排序
        else book[t++]=q[j++];
    }
    for(int i=l;i<=r;i++)q[i]=book[i];
    return;
}//并归排序
void solve(int l,int r){
    if(l==r)return;//递归边界，直接返回
    int mid=(l+r)>>1,t=l;
    solve(l,mid),solve(mid+1,r);//分治求解
    for(int i=mid+1;i<=r;i++){//指针扫描
        while(q[t].y<=q[i].y&&t<=mid)add(q[t].z,q[t].cnt),t++;//移动指针的同时，注意指针移动的范围，q[t].cnt指离散化前这种元素的数量
        q[i].ans+=ask(q[i].z);//更新答案
    }
    for(int i=l;i<t;i++)add(q[i].z,-q[i].cnt);//还原现场，注意是 i<t，以免多减
    return merge(l,mid,r),void();//并归排序
}

整体二分

没学不会。

点分治

点分治（又称淀粉质），通常用于统计树上路径。先看一道典题。

Tree

本题要求统计路径长度不超过 \(k\) 的路径数量，如果暴力统计，时间复杂度就会 TLE，思考优化的策略。

我们先选一个树中的节点 \(R\) 为这棵树的根节点，显然所有符合条件的路径可分为两类。

• 经过点 \(R\)，两端位于其两个不同的子节点的子树内。

• 整条路径在 \(R\) 的某个子节点的子树内。

我们发现这种路径很适合分治统计，很简单的就可以设计出分治算法的雏形。

1. 首先先选择树中一点 \(R\)，然后统计经过 \(R\) 的第二类路径。

2. 接着将 \(R\) 删除，使原本的一棵树变为若干棵树，再递归统计这些树中「路径长度不超过 \(k\) 的路径数量」。

注意在代码中的实现删除一般会打上标记，且在后续的统计中不会经过打了标记的节点。

我们先探讨第一步，给定一棵树，给定其根节点 \(R\)，如何快速统计出经过 \(R\) 的第二类路径？我们假定存在一条符合上述条件的路径 \(x\to y\)，则他们必然满足：

• \(x,y\) 分别属于 \(R\) 的不同子节点的子树

• \(R\to x,R\to y\) 的距离和不超过 \(k\)。

我们遍历整棵树，求出树中每个节点 \(x\) 的两个信息，分别是：输入根节点的那个儿子的子树（记为 \(b_x\)），到根节点的距离（记为 \(d_x\)）。合法路径条数其实就是在统计 \(b_x\ne b_y,d_x+d_y\le k\) 的无序点对 \((x,y)\) 的数量。

下面给出一种目前比较受欢迎的做法。

我们先不考虑 \(b_x\ne b_y\) 的限制条件，只求出 \(d_x+d_y\le k\) 的对数，我们记其为 \(\text{calc}(R)\)。我们可以先以 \(R\) 为根遍历整棵树，把所有的 \(d_x\) 求出来，然后用树状数组或双指针快速求解。

接下来做的就是要减去不合法的路径，设 \(R\) 有 \(h\) 个儿子，分别是 \(s_1,s_2,\dots,s_h\)，如果路径的两个端点 \((x,y)\) 都在 \(s_i\) 的子树中，则他们必然满足 \(\text{dis}(s_i,x)+\text{dis}(s_i,y)\le k-2\times \text{dis}(R,s_i)\)（\(\text{dis}(u,v)\) 表示两点之间的距离）。

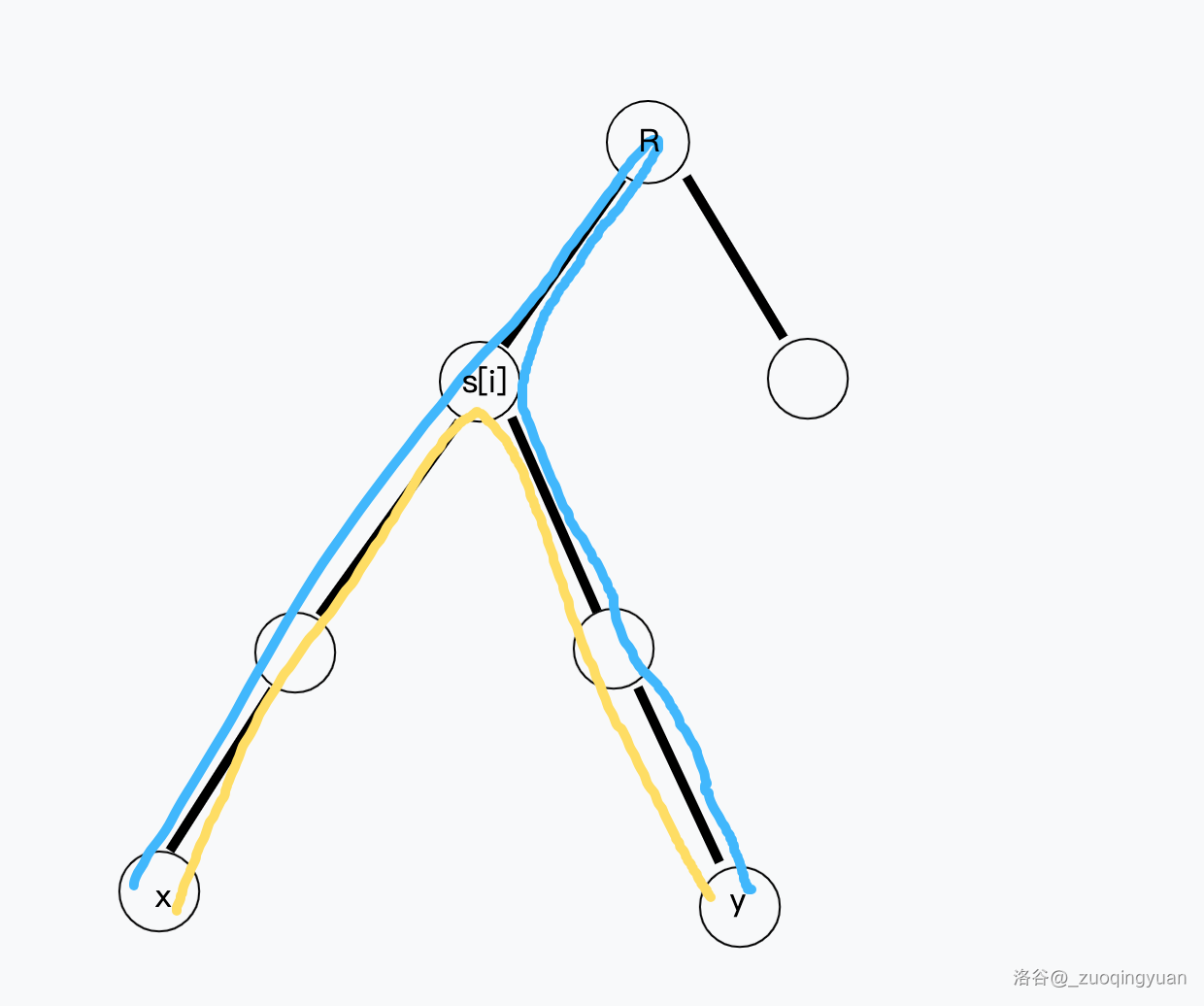
如上图，我们发现，统计中类似蓝色路径（所要求的不合法路径）的数量其实就是统计中类似黄色路径的数量，唯一不同的是蓝色路径统计的是在 \(R\) 中， $d_x+d_y\le k $ 的数量，而黄色路径则统计的是在 \(s_i\) 中，\(d_x+d_y\le k-2\times \text{dis}(R,s_i)\)，我们只需要先令答案加上 \(\text{calc}(R)\)，再挨个访问一遍 \(s_i\)，令答案减小 \(\text{calc}(s_i)\) 即可。具体的一些小问题看代码解决。

这种做法基于容斥原理，优势是易拓展，可以延伸到三维限制的统计中。劣势是时间复杂度稍差，理论上常数翻倍，实际时间上影响并不是很大。可以对比这一份和这一份的差异，前者是其他做法，没有用到容斥原理。

注意在执行 \(\text{calc}(R)\) 时，需注意 \(R\) 为合法路径端点时的情况。

在统计完第二类路径后，我们将节点 \(R\) 打上删除的标记，然后分别递归处理 \(R\) 各个子节点的子树。对于每颗需要统计的树，我们在分治时，都会选择一个分治中心，围绕这个中心统计路径，分治求解。

假设我们在执行完 \(\text{calc}(R)\)后，选择了 \(R_i'\) 作为处理 \(s_i\) 子树的新一轮分治中心。那么 \(R_i'\) 应当是子树中的那个点？如果单纯的选择 \(s_i\) 当做处理 \(s_i\) 子树的分治中心，那么恭喜，仍然喜提 TLE。当树退化成一条链时，时间复杂度会卡到 \(O(n^2)\)。

对于这个问题，我们可以选择子树的重心作为树的分治点，树重心有一个很好性质，就是删除重心后，原本的树分裂形成的新的树大小均不超过原树的一半，这相当于把分治的规模对半砍了一刀。

画出分治时的递归树，对于递归树中同一层深度分治函数所执行的 \(\text{calc}()\) 的扫描总共覆盖了整棵树一遍，所以递归树中同一层深度的分治函数总时间复杂度为 \(O(n\log n)\)，因为选择树的重心使得每一层分治和上一层相比规模减半，因此树高控制在 \(\log n\) 这个级别，总时间复杂度 \(O(n\log^2 n)\)。

搞定了这个，我们就完美的把这个问题解决了。

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N=4e4+10;
int n,idx,ver[N],to[2*N],nxt[2*N],val[2*N],k,siz[N],maxn[N],root,vis[N],cnt,b[N],ans,a[N];
void add(int x,int y,int z){
    to[++idx]=y,nxt[idx]=ver[x],ver[x]=idx,val[idx]=z;
}
int dfs_root(int x,int fa,int sum){
    siz[x]=1,maxn[x]=0;
    for(int i=ver[x];i;i=nxt[i]){
        if(vis[to[i]]||to[i]==fa)continue;
        siz[x]+=(siz[to[i]]=dfs_root(to[i],x,sum));
        maxn[x]=max(maxn[x],siz[to[i]]);
    }
    maxn[x]=max(maxn[x],sum-siz[x]);
    if(maxn[x]<maxn[root])root=x;
    return siz[x];
}//找树的重心
void dfs_dis(int x,int fa,int from,int len){
    a[++cnt]=len;
    for(int i=ver[x];i;i=nxt[i]){
        if(vis[to[i]]||to[i]==fa)continue;
        dfs_dis(to[i],x,from,len+val[i]);
    }
}//获得每个节点的信息
int calc(int u,int dist){
    a[cnt=1]=dist;//初始化以u为端点
    for(int i=ver[u];i;i=nxt[i]){
        if(vis[to[i]])continue;
        dfs_dis(to[i],u,to[i],dist+val[i]);
    }
    sort(a+1,a+1+cnt);
    int l=1,r=cnt,sum=0;
    while(l<r){
        while(a[l]+a[r]>k&&l<r)r--;
        sum+=(r-l),l++;
    }
    return sum;
}
void solve(int u){
    vis[u]=1;
    ans+=calc(u,0);
    for(int i=ver[u];i;i=nxt[i]){
        if(vis[to[i]])continue;
        ans-=calc(to[i],val[i]);//容斥
        root=0,dfs_root(to[i],u,siz[to[i]]);//递归分治
        solve(root);
    }
    return;
}
int main(){
    scanf("%d",&n);
    for(int i=1,u,v,w;i<n;i++){
        scanf("%d %d %d",&u,&v,&w);
        add(u,v,w),add(v,u,w);
    }
    scanf("%d",&k);
    maxn[0]=N;//注意初始化
    dfs_root(1,-1,n);
    solve(root);
    printf("%d\n",ans);
    return 0;
}