基于有限体积法和交错网格的SIMPLE算法推导及实现
SIMPLE算法,半隐式速度压力耦合算法,是专门求解不可压流体流动的算法。由于不可压流体控制方程中,密度常常被视为常数,没有表征流体密度、压力、温度联系的状态方程,压力以梯度项的形式存在于动量方程中,无法显性表达或者直接求解,造成了求解上的困难。因此需要对速度和压力进行解耦,其基本思想是,通过预设的压力场,代入到动量方程中,求解各方向上的速度场;然后根据质量守恒方程构建压力泊松方程,进行压力修正,再进行速度修正,反复迭代,直到达到预设的收敛条件。
交错网格
与交错网格相对的是同位网格,再RC插值方法提出之前,压力、速度都存于同一套网格中,共用网格节点。例如x方向的压力梯度项采用中心差分格式:
\[\frac{\partial P}{\partial x} = \frac{P_E - P_W}{2 \delta x} \]并没有使用到中心节点\(P_C\)的值,而在棋盘振荡的压力场时,很容易被认为是无压力梯度,即均匀压力场。造成脱离真实物理的情况。因此交错网格被提出,交错网格中,压力、温度、密度这一类标量存在一套网格中,而各方向上的速度则存在另外一套网格中,速度网格的中心与压力网格中心并不重合,存在一定偏差,速度网格中心一般定义在压力网格面的中心上。如果是均匀网格,则速度网格与压力网格偏差了“半个网格”。交错网格的优势很多,例如速度网格中心在压力网格面上,在求解压力修正方程时,不需要对速度再进行插值。避免了离散压力梯度存在的“棋盘格”问题。但是交错网格的致命缺陷就是使用非常复杂和繁琐,存储成本高,程序编制难度高,边界条件比较难处理,都是致命缺陷。
稳态二维各向同性流体动力学方程
二维情况下稳态动力学方程组如下:
\[\frac\partial{\partial x}(\rho uu)+\frac\partial{\partial y}(\rho vu)=\frac\partial{\partial x}\Bigg(\mu\frac{\partial u}{\partial x}\Bigg)+\frac\partial{\partial y}\Bigg(\mu\frac{\partial u}{\partial y}\Bigg)-\frac{\partial p}{\partial x}+S_u \]\[\frac\partial{\partial x}(\rho uv)+\frac\partial{\partial y}(\rho vv)=\frac\partial{\partial x}\Bigg(\mu\frac{\partial v}{\partial x}\Bigg)+\frac\partial{\partial y}\Bigg(\mu\frac{\partial v}{\partial y}\Bigg)-\frac{\partial p}{\partial y}+S_v \]连续性方程:
\[\frac\partial{\partial x}(\rho u)+\frac\partial{\partial y}(\rho v)=0 \]其中,对于各向同性的不可压流体而言,密度\(\rho\)和粘性系数\(\mu\)为常数,可以提出微分符号外,并进一步化简。使用交错网格,即标量、矢量(分量)分别存在一套网格中,彼此错位。但是,在列离散方程时,以变量为核心,以变量所处的网格为依据进行离散。例如,对x方向的动量方程进行离散,所求解的是速度的x分量\(u\),就以\(u\)网格为核心进行离散,所使用的网格编号就是\(u\)网格的网格编号。
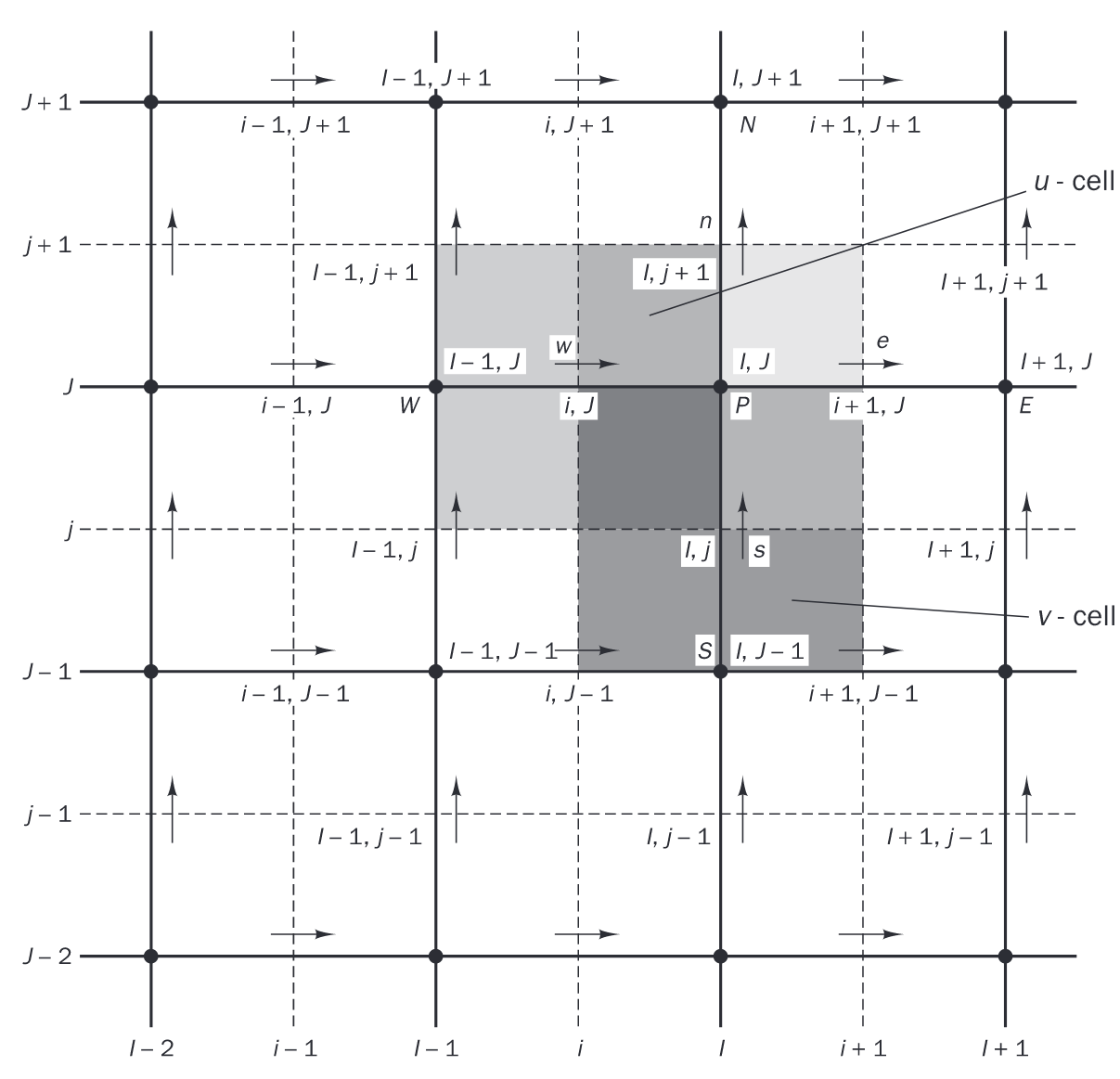
上图是交错网格的示意图,对应的是流场内部节点。速度u分量的网格中心(u-cell),刚好位于标量p(p-cell)网格的左右边界上,速度v分量的网格中心位于标量p网格的上下边界上。交错网格因为网格编号比较复杂,容易搞混,实际上只要记住一点,就可以理清楚三套网格的位置差异,即以行号i,列号j的p-cell网格为基准,行号i,列号j的u-cell网格在p-cell网格的左边界,行号i,列号j的v-cell网格在p-cell网格的右边界。记住这个转换关系就可以理清在程序编写时,同一i,j对于不同网格的相对位置关系。
动量方程离散
对对流项,采用一阶迎风格式,扩散项采用前向差分格式,注意,因为速度的方向是未知的,并不一定沿着坐标正方向,所以需要写成通用格式离散。首先忽略体积力源项,采用有限体积法对方程左右进行二维情况下的体积分,将方程进行半离散,可得:
\[\int {{{\left. {\rho uu} \right|}_e}dy} - \int {{{\left. {\rho uu} \right|}_w}dy} + \int {{{\left. {\rho vu} \right|}_n}dx} - \int {{{\left. {\rho vu} \right|}_s}dx} = \left( {\int {{{\left. {\mu \frac{{\partial u}}{{\partial x}}} \right|}_e}dy} - \int {{{\left. {\mu \frac{{\partial u}}{{\partial x}}} \right|}_w}dy} } \right) + \left( {\int {\mu {{\left. {\frac{{\partial u}}{{\partial y}}} \right|}_n}dx} - \int {\mu {{\left. {\frac{{\partial u}}{{\partial y}}} \right|}_s}dx} } \right) + \int { - \frac{{\partial p}}{{\partial x}}dxdy} \]将对流项和扩散项进行合并,再进行离散,以从u-cell右侧界面流入网格的通量为例:
\[\int {{{\left. {\rho uu} \right|}_e}dy} - \int {{{\left. {\mu \frac{{\partial u}}{{\partial x}}} \right|}_e}dy} = \left( {\left( {\frac{{{{\left| {\rho {u_{n - 1}}} \right|}_e} + {{\left. {\rho {u_{n - 1}}} \right|}_e}}}{2}} \right){u_P} - \left( {\frac{{{{\left| {\rho {u_{n - 1}}} \right|}_e} + {{\left. {\rho {u_{n - 1}}} \right|}_e}}}{2}} \right){u_E} - \frac{{{u_{E - }}{u_P}}}{{\Delta x}}} \right)\Delta y \]上式中,\(\rho u_{n-1}\)为质量通量,由于原本的\(\rho u u\)为非线性项,直接迭代较为困难。所以这里采用延迟修正,即使用上一步迭代计算得到的速度,来计算质量通量。当迭代残差越小时,上一步迭代的结果越接近当前迭代步计算得到的结果,实现一种类似“追赶”效果,直到两者误差在可接受范围内。\(u_P\)为当前u-cell网格中的u速度,\(u_E\)为右侧u-cell中心的u速度。\(\int {{{\left. {\rho uu} \right|}_e}dy}\)采用一阶迎风格式进行离散。而\(\int {{{\left. {\mu \frac{{\partial u}}{{\partial x}}} \right|}_e}dy}\)则使用了前向差分,一阶格式进行离散得到。这里\(\mu\)被认为是一个常数,简化了运算,否则,\(\mu\)实际上需要被当做一个场量来处理,需要通过紧邻点的\(\mu\)值得到。
注意\(\rho u_{n-1}\)是u-cell右侧边界上的通量值,它仍然需要通过插值来获得,如下图所示:
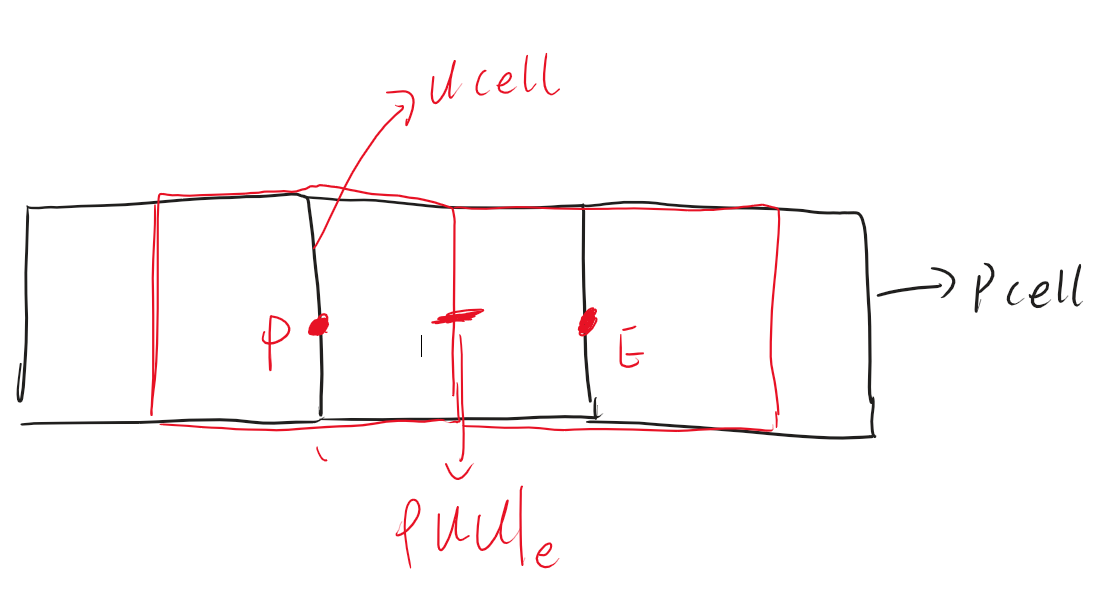
通过对界面邻近网格的体心值进行插值可以得到界面上的值:
\[\rho u_{n-1} = \rho\frac{u_P^{n-1} + u_E^{n-1}}{2} \]因为流体是均质不可压流体,密度被设为常数。
同理可得其余项的离散方程:
\[\int {{{\left. {\rho uu} \right|}_w}dy} - \int {{{\left. {\mu \frac{{\partial u}}{{\partial x}}} \right|}_w}dy} = \left( {\left( {\frac{{{{\left| {\rho {u_{n - 1}}} \right|}_w} + {{\left. {\rho {u_{n - 1}}} \right|}_w}}}{2}} \right){u_W} - \left( {\frac{{{{\left| {\rho {u_{n - 1}}} \right|}_e} - {{\left. {\rho {u_{n - 1}}} \right|}_e}}}{2}} \right){u_P} - \frac{{{u_{P - }}{u_W}}}{{\Delta x}}} \right)\Delta y \]\[\int {{{\left. {\rho vu} \right|}_n}dy} - \int {{{\left. {\mu \frac{{\partial u}}{{\partial y}}} \right|}_n}dx} = \left( {\left( {\frac{{{{\left| {\rho {v_{n - 1}}} \right|}_n} + {{\left. {\rho {v_{n - 1}}} \right|}_n}}}{2}} \right){u_P} - \left( {\frac{{{{\left| {\rho {v_{n - 1}}} \right|}_n} - {{\left. {\rho {v_{n - 1}}} \right|}_n}}}{2}} \right){u_P} - \frac{{{u_{N - }}{u_P}}}{{\Delta y}}} \right)\Delta x \]\[\int {{{\left. {\rho vu} \right|}_s}dy} - \int {{{\left. {\mu \frac{{\partial u}}{{\partial y}}} \right|}_s}dx} = \left( {\left( {\frac{{{{\left| {\rho {v_{n - 1}}} \right|}_s} + {{\left. {\rho {v_{n - 1}}} \right|}_s}}}{2}} \right){u_S} - \left( {\frac{{{{\left| {\rho {v_{n - 1}}} \right|}_s} - {{\left. {\rho {v_{n - 1}}} \right|}_s}}}{2}} \right){u_P} - \frac{{{u_{P - }}{u_S}}}{{\Delta y}}} \right)\Delta x \]这里,涉及到\(\rho v_{n-1}\),需要找到对应的v-cell网格进行插值得到,如下图所示:
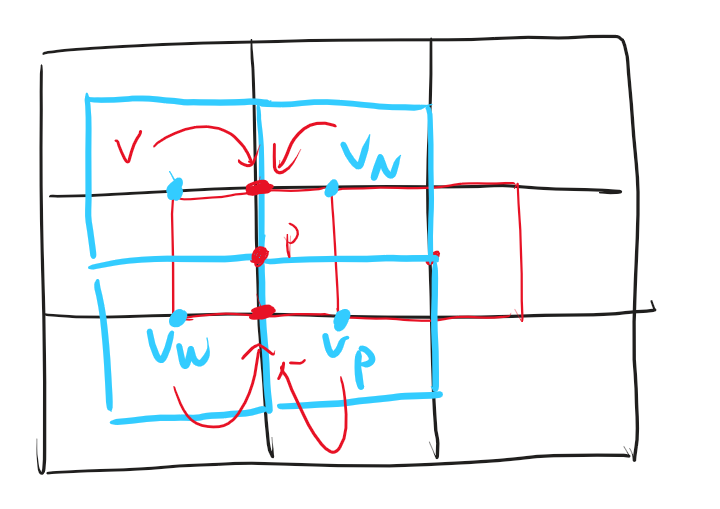
蓝色为v-cell,红色为u-cell,u-cell的上下界面的质量通量,,假定\(u_P\)的网格索引号为i,j,则对应到v-cell网格中的索引如下,\(\rho v_{n-1}\)通过相邻v-cell的体心值插值获得:
\[\rho v_{n-1}|_{s}=\rho\frac{v_P+v_W}{2}=\rho\frac{v_{i,j}+v_{i,j-1}}{2} \]\[\rho v_{n-1}|_{n}=\rho\frac{v_N+v}{2}=\rho\frac{v_{i+1,j}+v_{i+1,j-1}}{2} \]最后是压力梯度项的离散,这里需要说明,虽然此处是对压力梯度进行离散,但是求解的变量为u,以u-cell的位置为基准进行离散,这里体现出一个交错网格的优势,它十分巧妙的让几套网格的中心落在边界上。u-cell的中心,其实是压力网格的左边界。因此以u-cell为中心的压力梯度离散,可以直接采用p-cell的体心值前向差分得到,不需要像上述过程在边界处再插值:
\[\int \frac{\partial p}{\partial x}dxdy= (P_P-P_W)\Delta y \]同理对y方向上的动量方程也进行上述离散过程,不再赘述。对上述格式进行整理可以获得:
\[a_{{i,\tilde{f}}}u_{{i,\tilde{f}}}=\sum a_{nb}u_{nb}-({p_{I,\tilde{f}}-p_{I-1,\tilde{f}}})\Delta y \]\[a_{I,j}v_{I,j}=\sum a_{nb}v_{nb}+(p_{I,j-1}-p_{I,j})\Delta x \]SIMPLE算法速度和压力修正
接下来是SIMPLE算法的核心步骤:
假定\(u^*\)和\(v^*\)为某一迭代步计算后得到的解,则有(\(A_{ij}\)即\(\Delta x\)、\(\Delta y\)):
\[a_{i,f}u_{i,f}^*=\sum a_{nb}u_{nb}^*+(p_{I-1,f}^*-p_{I,f}^*)A_{i,f}+b_{i,f} \]\[a_{I,j}v_{I,j}^*=\sum a_{nb}v_{nb}^*+(p_{I,j-1}^*-p_{I,j}^*)A_{I,j}+b_{I,j} \]将上式与假定的收敛解做差,可得:
\[a_{{i,j}}(u_{{i,j}}-u_{{i,j}}^{*})=\sum a_{nb}(u_{nb}-u_{nb}^{*})+[(p_{{I-1,j}}-p_{{I-1,j}}^{*})-(p_{{I,j}}-p_{{I,j}}^{*})]A_{{i,j}} \]\[a_{I,j}(v_{I,j}-v_{I,j}^{*})=\sum a_{nb}(v_{nb}-v_{nb}^{*})+[(p_{I,j-1}-p_{I,j-1}^{*})-(p_{I,j}-p_{I,j}^{*})]A_{I,j} \]进一步简写可以得到:
\[a_{i,j}u_{i,j}^{\prime}=\sum a_{nb}u_{nb}^{\prime}+(p_{I-1,j}^{\prime}-p_{I,j}^{\prime})A_{i,j}\\a_{I,j}v_{I,j}^{\prime}=\sum a_{nb}v_{nb}^{\prime}+(p_{I,j-1}^{\prime}-p_{I,j}^{\prime})A_{I,j} \]上式中,\(u_{i,j}^{\prime}\)和\(v_{I,j}^{\prime}\)则分别是u-cell和v-cell速度修正值,因此速度的更新,则由迭代值\(u^*\)和\(u^{\prime}\)决定:
\[u=u^*+u^{\prime} \]\[v=v^{*}+v^{\prime} \]上式中,\(\sum a_{nb}(u_{nb}-u_{nb}^{*})\)为相邻网格节点对速度修正值的影响。SIMPLE算法在迭代过程中,将这一值忽略,即速度修正仅与压力修正值有关。这样做,近邻点无法显性表达,直接迭代处理较为麻烦,二是,随着速度逐渐收敛,近邻点的影响逐渐减弱,直到“忽略不计”,并不会影响最终的结果:
\[u_{i,j}^{\prime}=d_{i,j}(p_{I-1,j}^{\prime}-p_{I,j}^{\prime})\\v_{I,j}^{\prime}=d_{I,j}(p_{I,j-1}^{\prime}-p_{I,j}^{\prime}) \]\[u_{i,j}=u_{i,j}^*+d_{i,j}(p_{i-1,j}^\prime-p_{i,j}^\prime) \]\[v_{I,j}=v_{I,j}^*+d_{I,j}(p_{I,j-1}^{\prime}-p_{I,j}^{\prime}) \]到这一步,我们终于把压力修正值与速度修正值联系起来了。可是仅靠动量方程,我们还是无法得到将两者求解出来。这时,还剩下连续性方程,连续性方程没有压力表达式的参与,仅由速度和密度决定。更像是一个准确性判据,即速度必须需要满足连续性方程,才是符合物理解的方程。
\[[(\rho uA)_{i+1,j}-(\rho uA)_{i,j}]+[(\rho vA)_{I,j+1}-(\rho vA)_{I,j}]=0 \]将u和v的迭代表达式代入上述方程,可以得到压力泊松方程:
\[\begin{aligned}&[\rho_{i+1,j}A_{i+1,j}(u_{i+1,j}^{*}+d_{i+1,j}(p_{I,j}^{\prime}-p_{I+1,j}^{\prime}))-\rho_{i,j}A_{i,j}(u_{i,j}^{*}\\&+d_{i,j}(p_{I-1,j}^{\prime}-p_{I,j}^{\prime}))]+[\rho_{I,j+1}A_{I,j+1}(v_{I,j+1}^{*}+d_{I,j+1}(p_{I,j}^{\prime}-p_{I,j+1}^{\prime}))\\&-\rho_{I,j}A_{I,j}(v_{I,j}^{*}+d_{I,j}(p_{I,j-1}^{\prime}-p_{I,j}^{\prime}))]=0\end{aligned} \]进一步化简得到:
\[a_{I,j}p_{I,j}^{\prime}=a_{I+1,j}p_{I+1,j}^{\prime}+a_{I-1,j}p_{I-1,j}^{\prime}+a_{I,j+1}p_{I,j+1}^{\prime}+a_{I,j-1}p_{I,j-1}^{\prime}+b_{I,j}^{\prime} \]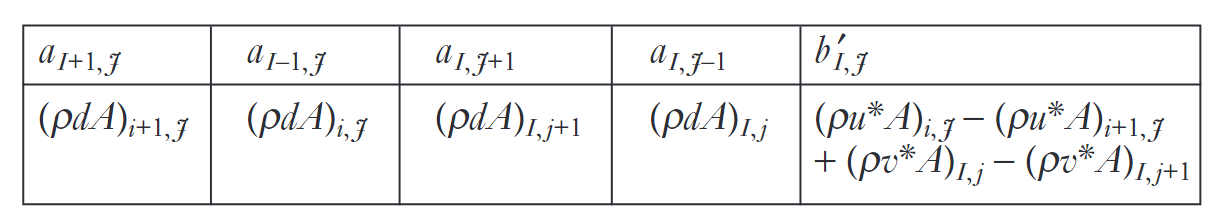
压力泊松方程,求解的是各个节点上的压力修正值。仍然是需要迭代求解,并非显性可以直接递推获得全域的压力修正值。
边界条件
边界条件应该是交错网格中,最容易让人误判的地方,参考书目中对边界条件讲的并不太多。首先,这是与交错网格划分方式相关。一般而言,对于真实流体域划分网格,以标量网格为核心,速度网格再错开。如下图所示:
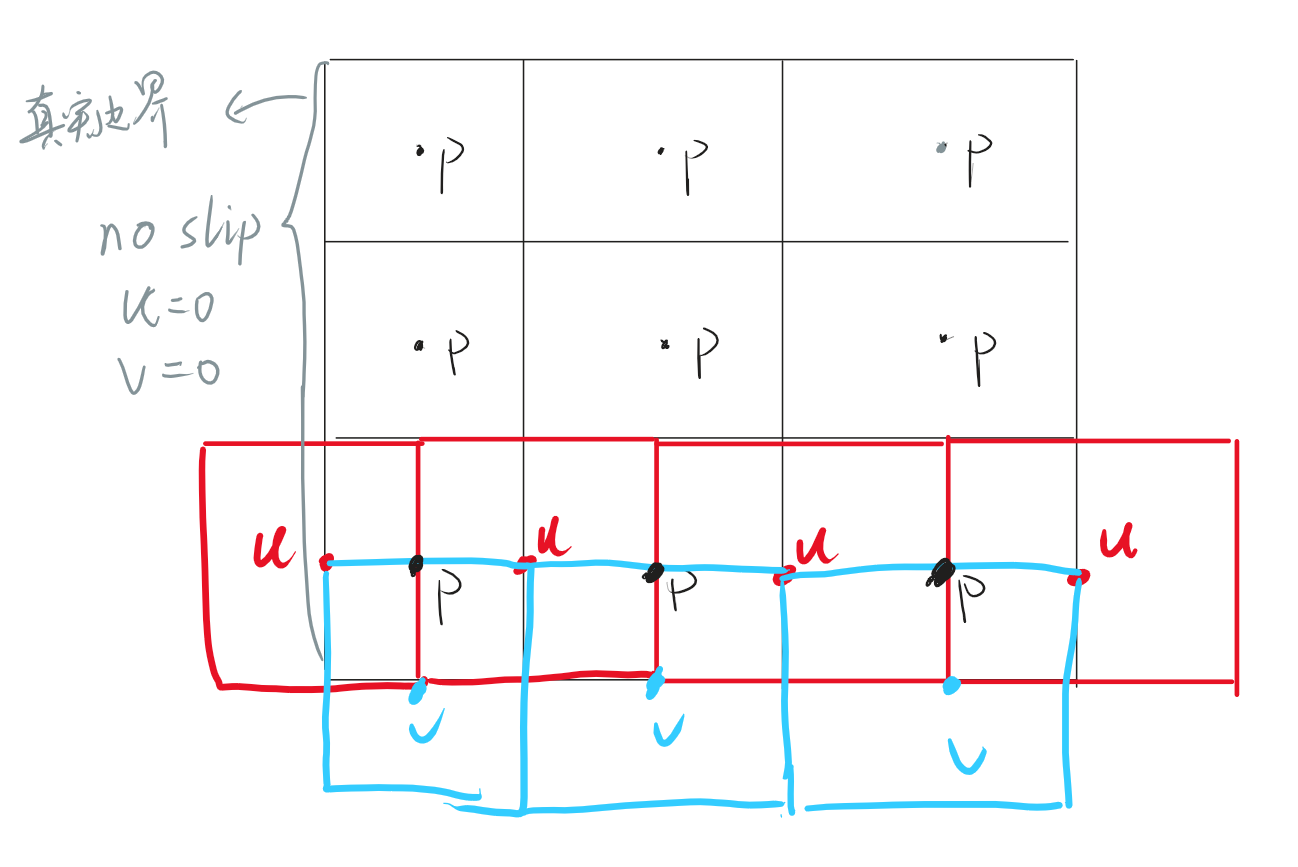
以压力网格为核心,速度网格u和v相对于p网格中心进行偏移。对于无滑移边界条件而言,边界上的速度值已经给定,而u和v的边界网格中心,刚好落在物理边界上。所以直接对速度网格赋予边界值,在求解压力泊松方程。
而对于p网格,其边界条件的确定,则对应到压力泊松方程,具体参考汪洋博士的开源文档(B站名:大官人学CFD)。
本文所使用的网格划分方式,与上述方式略有不用,更"类似"于有限差分法的网格划分方式,即p-cell的中心在物理边界上,导致边界上的速度网格向外延伸,超出边界成为虚拟网格。
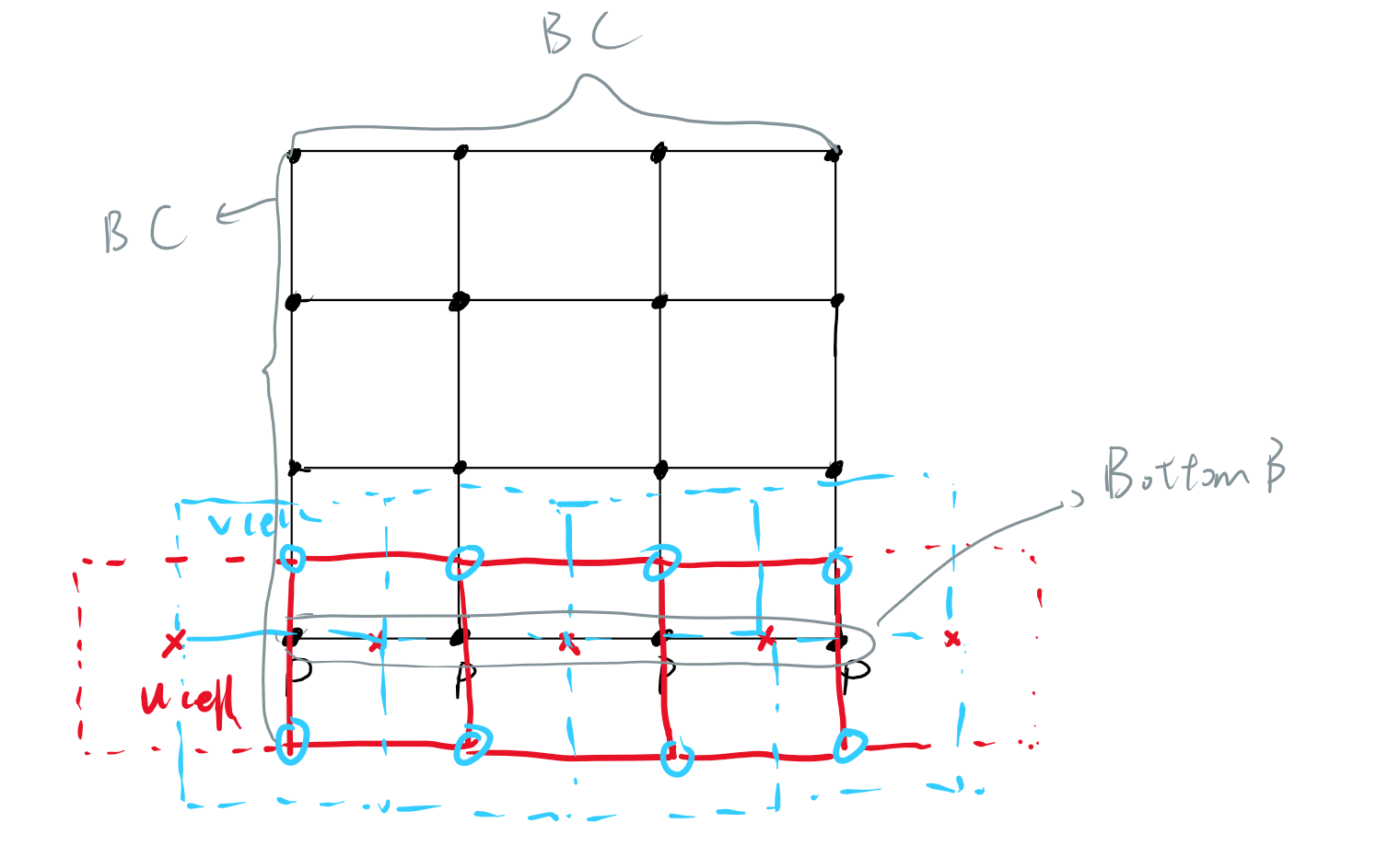
对于u网格(上图中红色网格):
u网格在左右边界向外延伸出一个虚拟网格节点,而在上下边界中,则u-cell中心落在边界上,因此对于无滑移边界或者速度给定的边界条件,则,上下边界的u-cell网格可以直接给定速度值。而对于左右边界,超出实际物理边界的虚拟边界网格的赋值,则认为与内层节点互为相反数(对于无滑移边界)。因为物理边界实际处于虚拟节点与内层节点的中心位置,u=0,所以根据插值关系得到虚拟节点的赋值与内层节点的计算值互为相反数。
对于v网格(上图中蓝色网格):
与u网格处理方式极为相似,不同的是,计算域左右物理边界,刚好处于v网格的中心位置,所以可以直接赋值。而上下边界处,v网格向外延伸出一层虚拟节点,和u网格处理方法一致,在无滑移边界条件下,边界虚拟网格节点的值与内层网格节点值互为相反数。
对于p网格(上图中黑色网格):
对于p网格,要分情况讨论,还是要落到原本的压力修正方程中。四个角点的p网格,首先考虑到,压力是一个相对意义大于绝对意义的物理量,CFD计算中关注压差,而非绝对压力,压差是驱动流体运动的关键。计算压力需要设置一个压力参考点,由于上边界设定为速度边界,所以习惯性设定左下角角点处的压力为0,作为一个计算参考值。
紧接着对于其余3个角点,将网格边界上的通量代入到原本压力修正方程中,可以得到,对于右下角角点,AE=0,AS=0。左上角角点,AW=0,AN=0。右上角角点,AN=0,AE=0。
然后是除角点外的边界网格,对于左边界,AW=0;右边界,AE=0;上边界,AN=0;下边界, AS = 0。
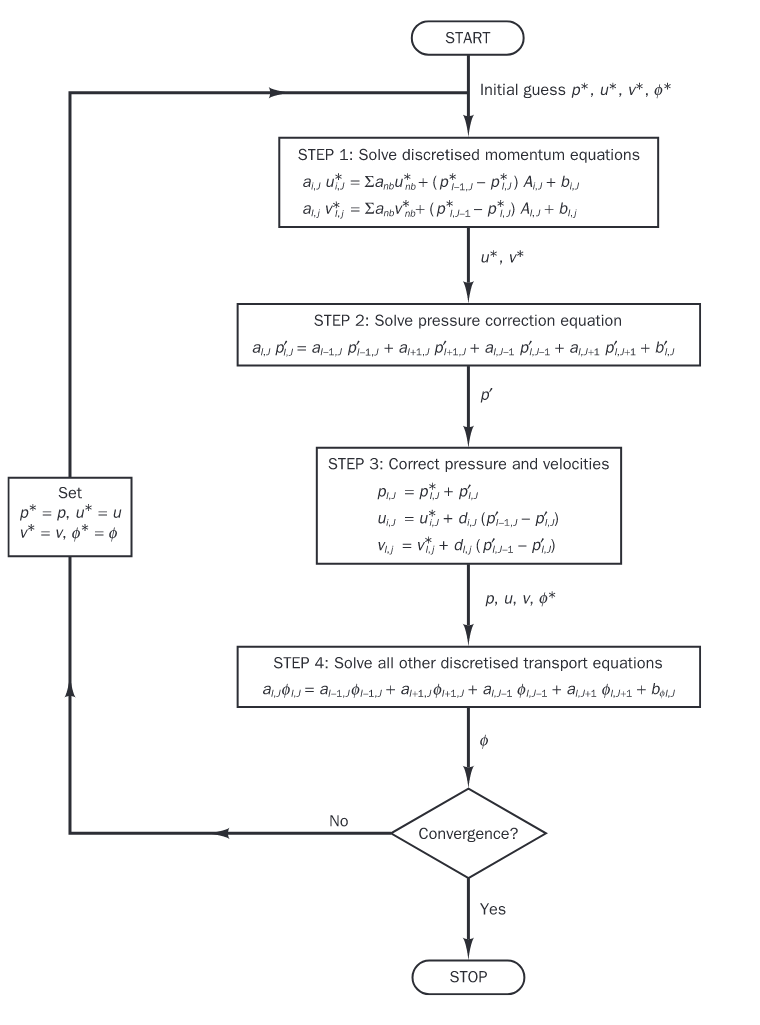
最后是SIMPLE算法的流程:
计算程序
以二维驱动方腔流动为例,编写程序,实现使用有限体积法和交错网格计算方腔内的速度和压力分布(个人觉得最难的部分,其实还是在于边界条件的理解上):
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Sun Apr 28 09:46:16 2024
@author: mestro
"""
from math import *
import numpy as np
import matplotlib.pyplot as plt
L = 1.0
N = 51
dx = L/(N-1)
dy = L/(N-1)
velocity = 2.0
rho = 1
miu = 0.01
P = np.zeros([N,N])
U = np.zeros([N,N+1])
V = np.zeros([N+1,N])
U[N-1,:] = velocity
dU = np.zeros([N,N+1])
dV = np.zeros([N+1,N])
P_iter = P.copy()
U_iter = U.copy()
V_iter = V.copy()
NN = N*N
iter = 0
err = 1.0
while (iter < 1000) and (err > 1e-5):
for i in range(1,N-1):
for j in range(1,N):
rho_u_e = 0.5*(U[i,j] + U[i,j+1])*rho;
rho_u_w = 0.5*(U[i,j] + U[i,j-1])*rho;
rho_v_s = 0.5*(V[i,j] + V[i,j-1])*rho;
rho_v_n = 0.5*(V[i+1,j] + V[i+1,j-1])*rho;
AE = 0.5*(abs(rho_u_e) + rho_u_e)*dy + miu*dy/dx;
AW = 0.5*(abs(rho_u_w) - rho_u_w)*dy + miu*dy/dx;
AN = 0.5*(abs(rho_v_n) + rho_v_n)*dx + miu*dx/dy;
AS = 0.5*(abs(rho_v_s) - rho_v_s)*dx + miu*dx/dy;
AEE = 0.5*(abs(rho_u_e) - rho_u_e)*dy + miu*dy/dx;
AWW = 0.5*(abs(rho_u_w) + rho_u_w)*dy + miu*dy/dx;
ANN = 0.5*(abs(rho_v_n) - rho_v_n)*dx + miu*dx/dy;
ASS = 0.5*(abs(rho_v_s) + rho_v_s)*dx + miu*dx/dy;
Ap = (AE+AW+AN+AS);
U_iter[i,j] = 1/Ap*(AEE*U[i,j+1] + AWW*U[i,j-1] + ANN*U[i+1,j] + ASS*(U[i-1,j]) - (P[i,j] - P[i,j-1])*dy);
dU[i,j] = dy/Ap;
#bottom mesh
i = 0;
for j in range(1,N):
rho_u_e = 0.5*(U[i,j] + U[i,j+1])*rho;
rho_u_w = 0.5*(U[i,j] + U[i,j-1])*rho;
#rho_v_s = 0.5*(V[i,j] + V[i,j-1])*rho;
rho_v_n = 0.5*(V[i+1,j] + V[i+1,j-1])*rho;
AE = 0.5*(abs(rho_u_e) + rho_u_e)*dy + miu*dy/dx;
AW = 0.5*(abs(rho_u_w) - rho_u_w)*dy + miu*dy/dx;
AN = 0.5*(abs(rho_v_n) + rho_v_n)*dx + miu*dx/dy;
#AS = 0.5*(abs(rho_v_s) - rho_v_s)*dx + miu*dx/dy;
As = 0;
Ap = (AE+AW+AN+AS);
dU[i,j] = dy/Ap;
#top mesh
i = N-1
for j in range(1,N):
rho_u_e = 0.5*(U[i,j] + U[i,j+1])*rho;
rho_u_w = 0.5*(U[i,j] + U[i,j-1])*rho;
rho_v_s = 0.5*(V[i,j] + V[i,j-1])*rho;
#rho_v_n = 0.5*(V[i+1,j] + V[i+1,j-1])*rho;
AE = 0.5*(abs(rho_u_e) + rho_u_e)*dy + miu*dy/dx;
AW = 0.5*(abs(rho_u_w) - rho_u_w)*dy + miu*dy/dx;
#AN = 0.5*(abs(rho_v_n) + rho_v_n)*dx + miu*dx/dy;
AN = 0.0;
AS = 0.5*(abs(rho_v_s) - rho_v_s)*dx + miu*dx/dy;
Ap = (AE+AW+AN+AS);
dU[i,j] = dy/Ap;
#Apple BCs
U_iter[:,0] = -U_iter[:,1]; #left
U_iter[1:N-1,N] = -U_iter[1:N-1,N-1]; #right
U_iter[0,:] = 0.0 #bottom
U_iter[N-1,:] = velocity #top
# V equation
for i in range(1,N):
for j in range(1,N-1):
rho_u_e = 0.5*(U[i,j] + U[i-1,j])*rho;
rho_u_w = 0.5*(U[i,j+1] + U[i-1,j+1])*rho;
rho_v_n = 0.5*(V[i,j] + V[i+1,j])*rho;
rho_v_s = 0.5*(V[i,j] + V[i-1,j])*rho;
AE = 0.5*(abs(rho_u_e) + rho_u_e)*dy + miu*dy/dx;
AW = 0.5*(abs(rho_u_w) - rho_u_w)*dy + miu*dy/dx;
AN = 0.5*(abs(rho_v_n) + rho_v_n)*dx + miu*dx/dy;
AS = 0.5*(abs(rho_v_s) - rho_v_s)*dx + miu*dx/dy;
AEE = 0.5*(abs(rho_u_e) - rho_u_e)*dy + miu*dy/dx;
AWW = 0.5*(abs(rho_u_w) + rho_u_w)*dy + miu*dy/dx;
ANN = 0.5*(abs(rho_v_n) - rho_v_n)*dx + miu*dx/dy;
ASS = 0.5*(abs(rho_v_s) + rho_v_s)*dx + miu*dx/dy;
Ap = (AE+AW+AN+AS);
V_iter[i,j] = 1.0/Ap*(AEE*V[i,j+1] + AWW*V[i,j-1] + ANN*V[i+1,j] + ASS*V[i-1,j] - (P[i,j] - P[i-1,j])*dx);
dV[i,j] = dx/Ap;
#left
j = 0
for i in range(1,N):
rho_u_e = 0.5*(U[i,j] + U[i-1,j])*rho;
#rho_u_w = 0.5*(U[i,j+1] + U[i-1,j+1])*rho;
rho_v_n = 0.5*(V[i,j] + V[i+1,j])*rho;
rho_v_s = 0.5*(V[i,j] + V[i-1,j])*rho;
AE = 0.5*(abs(rho_u_e) + rho_u_e)*dy + miu*dy/dx;
#AW = 0.5*(abs(rho_u_w) - rho_u_w)*dy + miu*dy/dx;
AW = 0.0
AN = 0.5*(abs(rho_v_n) + rho_v_n)*dx + miu*dx/dy;
AS = 0.5*(abs(rho_v_s) - rho_v_s)*dx + miu*dx/dy;
Ap = (AE+AW+AN+AS);
dV[i,j] = dx/Ap;
#right0, L, N
j = N-1
for i in range(1,N):
#rho_u_e = 0.5*(U[i,j] + U[i-1,j])*rho;
rho_u_w = 0.5*(U[i,j+1] + U[i-1,j+1])*rho;
rho_v_n = 0.5*(V[i,j] + V[i+1,j])*rho;
rho_v_s = 0.5*(V[i,j] + V[i-1,j])*rho;
#AE = 0.5*(abs(rho_u_e) + rho_u_e)*dy + miu*dy/dx;
AE = 0.0;
AW = 0.5*(abs(rho_u_w) - rho_u_w)*dy + miu*dy/dx;
AN = 0.5*(abs(rho_v_n) + rho_v_n)*dx + miu*dx/dy;
AS = 0.5*(abs(rho_v_s) - rho_v_s)*dx + miu*dx/dy;
Ap = (AE+AW+AN+AS);
dV[i,j] = dx/Ap;
#Apply BCs
V_iter[:,0] = 0.0;
V_iter[:,N-1] = 0.0;
V_iter[0,1:N-1] = -V_iter[1,1:N-1];
V_iter[N,1:N-1] = -V_iter[N-1,1:N-1];
U_old = U.copy();
V_old = V.copy();
bp = np.zeros([NN,1]);
#pressure fix
for i in range(N):
for j in range(N):
index = i*N+j;
bp[index] = (rho*U_iter[i,j]*dy - rho*U_iter[i,j+1]*dy + rho*V_iter[i,j]*dx - rho*V_iter[i+1,j]*dx);
bp[0] = 0.0;
APP = np.zeros([NN,NN]);
#left bottom
i = 0
j = 0
index = i*N + j
# Ae = -rho*dU[i,j+1]*dy;
# An = -rho*dV[i+1,j]*dx;
# Ap = -(Ae + An);
# APP[index,index+1] = Ae;
# APP[index,index+N] = An;
# APP[index,index] = Ap;
APP[index,index] = 1;
#right bottom
i = 0;
j = N-1;
index = i*N + j
Aw = -rho*dU[i,j]*dy;
An = -rho*dV[i+1,j]*dx;
Ap = -(Aw + An);
APP[index,index - 1] = Aw;
APP[index,index + N] = An;
APP[index,index] = Ap;
#left top
i = N-1
j = 0;
index = i*N + j
As = -rho*dV[i,j]*dx;
Ae = -rho*dU[i,j+1]*dy;
Ap = -(As + Ae);
APP[index,index+1] = Ae;
APP[index,index-N] = As;
APP[index,index] = Ap;
#right top
i = N-1
j = N-1
index = i*N+j
Aw = -rho*dU[i,j]*dy;
As = -rho*dV[i,j]*dx;
Ap = -(Aw + As);
APP[index,index] = Ap
APP[index,index-1] = Aw
APP[index,index-N] = As
i = 0;
for j in range(1,N-1):
index = i*N+j;
Aw = -rho*dU[i,j]*dy;
An = -rho*dV[i+1,j]*dx;
Ae = -rho*dU[i,j+1]*dy;
Ap = -(Aw + An + Ae);
APP[index,index] = Ap;
APP[index,index-1] = Aw;
APP[index,index+N] = An;
APP[index,index+1] = Ae;
i = N-1;
for j in range(1,N-1):
index = i*N+j
Aw = -rho*dU[i,j]*dy;
As = -rho*dV[i,j]*dx;
Ae = -rho*dU[i,j+1]*dy;
Ap = -(Aw + As + Ae);
APP[index,index] = Ap;
APP[index,index - 1] = Aw;
APP[index,index - N] = As;
APP[index,index + 1] = Ae;
j = 0;
for i in range(1,N-1):
index = i*N+j;
Ae = -rho*dU[i,j+1]*dy;
An = -rho*dV[i+1,j]*dx;
As = -rho*dV[i,j]*dx;
Ap = -(Ae + An + As);
APP[index,index] = Ap;
APP[index,index + 1] = Ae;
APP[index,index + N] = An;
APP[index,index - N] = As;
j = N-1;
for i in range(1,N-1):
index = i*N + j;
Aw = -rho*dU[i,j]*dy;
An = -rho*dV[i+1,j]*dx;
As = -rho*dV[i,j]*dx;
Ap = -(Aw + An + As);
APP[index,index] = Ap;
APP[index,index - 1] = Aw;
APP[index,index + N] = An;
APP[index,index - N] = As;
for i in range(1,N-1):
for j in range(1,N-1):
index = i*N + j
Aw = -rho*dU[i,j]*dy;
An = -rho*dV[i+1,j]*dx;
As = -rho*dV[i,j]*dx;
Ae = -rho*dU[i,j+1]*dy;
Ap = -(Aw + An + As + Ae);
APP[index,index] = Ap;
APP[index,index - 1] = Aw;
APP[index,index + N] = An;
APP[index,index - N] = As;
APP[index,index + 1] = Ae;
# pressure correction
p_fix = np.linalg.solve(APP, bp)
P_fix_matrix = np.zeros([N,N]);
for i in range(N):
for j in range(N):
index = i*N+j
P[i,j] = 0.3*p_fix[index] + P[i,j];
P_fix_matrix[i,j] = p_fix[index];
P[0,0] = 0.0;
#velocity update
for i in range(1,N-1):
for j in range(1,N):
U[i,j] = U_iter[i,j] + dU[i,j]*(P_fix_matrix[i,j-1] - P_fix_matrix[i,j]);
for i in range(1,N):
for j in range(1,N-1):
V[i,j] = V_iter[i,j] + dV[i,j]*(P_fix_matrix[i-1,j] - P_fix_matrix[i,j]);
#Apple BCs
U[1:N-1,0] = -U[1:N-1,1]; #left
U[1:N-1,N] = -U[1:N-1,N-1]; #right
U[0,:] = 0.0 #bottom
U[N-1,:] = velocity #top
V[0,1:N-1] = -V[1,1:N-1];
V[N,1:N-1] = -V[N-1,1:N-1];
V[:,0] = 0.0;
V[:,N-1] = 0.0;
err1 = np.max(np.abs(U-U_old))
err2 = np.max(np.abs(V-V_old))
err = max(err1,err2)
iter = iter + 1
print("the iter num is " + str(iter) + " and max err is " + str(err) + "\n")
#plot
x = np.linspace(dx/2, 1 - dx/2,N-1);
y = np.linspace(0, 1, N)
X, Y = np.meshgrid(x, y) # Generate 2D grid coordinates
plt.figure()
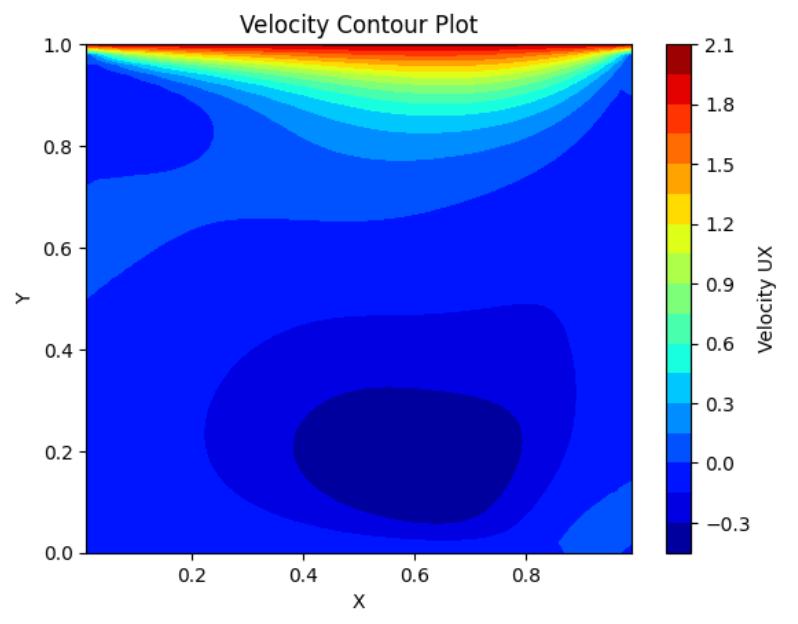
plt.contourf(X,Y, U[:,1:N], levels=20, cmap='jet') # Adjust levels and cmap as needed
plt.colorbar(label='Velocity UX')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Velocity Contour Plot')
plt.show()
x = np.linspace(0,1,N);
y = np.linspace(0, 1, N)
X, Y = np.meshgrid(x, y) # Generate 2D grid coordinates
plt.figure()
plt.contourf(X,Y,P, levels=20, cmap='jet') # Adjust levels and cmap as needed
plt.colorbar(label='pressure P')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Pressure')
plt.show()
小结
本文主要是使用Python实现了基于有限体积法和交错网格的SIMPLE算法,对流项采用一阶迎风格式,扩散项采用前向差分,其实离散过程并不复杂,最复杂和最难分清楚的还是在于边界条件,个人觉得这也是书中讲述比较少的地方。文中有错误非常欢迎指出,尤其是理解上和原则性错误。文章会同步到个人博客(https://bihengx.github.io)
参考资料:
- B站 曾导SJTU的CFD从0到1的课程
- B站 大官人学CFD,汪洋博士的开源OpenFOAM基础课程讲义
- 参考书:An Introduction to Computational Fluid Dynamics The Finite Volume Method 2nd Edition.