蓝桥杯算法集训 - Week 5
本系列随笔用于整理AcWing题单——《蓝桥杯集训·每日一题2024》的系列题型及其对应的算法模板。
一、树状数组
树状数组是一种数据结构,可以快速地完成以下两个操作:
- 将第 i 个数加上 c
- 快速求前缀和,即任意区间[i,j]的和
Ⅰ、代码模板
// 树状数组长度是固定的,为 n+1
// 树状数组的下标必须从 1 开始
static int[] tr = new int[n + 1];
// 求最低的一位 1
static int lowbit(int x){
return x & -x;
}
// 在 tr[x] 的位置加上c
static void add(int x, int c){
for(int i = x; i <= n; i += lowbit(i))
tr[i] += c;
}
// 查询前缀和
static int query(int x){
int res = 0;
for(int i = x; i > 0; i -= lowbit(i))
res += tr[i];
return res;
}
Ⅱ、动态求连续区间和

import java.io.*;
public class Main {
static final int N = 100010;
static int n, m;
static int[] a = new int[N], tr = new int[N];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] split = br.readLine().split(" ");
n = Integer.parseInt(split[0]);
m = Integer.parseInt(split[1]);
split = br.readLine().split(" ");
for (int i = 1; i <= n; i++) {
a[i] = Integer.parseInt(split[i - 1]);
}
// 初始化 tr 数组
for (int i = 1; i <= n; i++) {
add(i, a[i]);
}
for (int i = 0; i < m; i++) {
split = br.readLine().split(" ");
int o = Integer.parseInt(split[0]);
int a = Integer.parseInt(split[1]);
int b = Integer.parseInt(split[2]);
if (o == 0) {
System.out.println(query(b) - query(a - 1)); // 通过 tr 前缀和求区间和
} else {
add(a, b); // 修改单个元素
}
}
br.close();
}
static int lowbit(int x) {
return x & -x;
}
static void add(int x, int c) {
for (int i = x; i <= n; i += lowbit(i)) {
tr[i] += c;
}
}
static int query(int x) {
int res = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
res += tr[i];
}
return res;
}
}
二、DP入门
对应2024蓝桥杯每日一题 Week 5 星期三 线性DP。
DP 算法复习参考资料:第 14 章 动态规划 - Hello 算法
Ⅰ、打家劫舍

闫式DP分析法
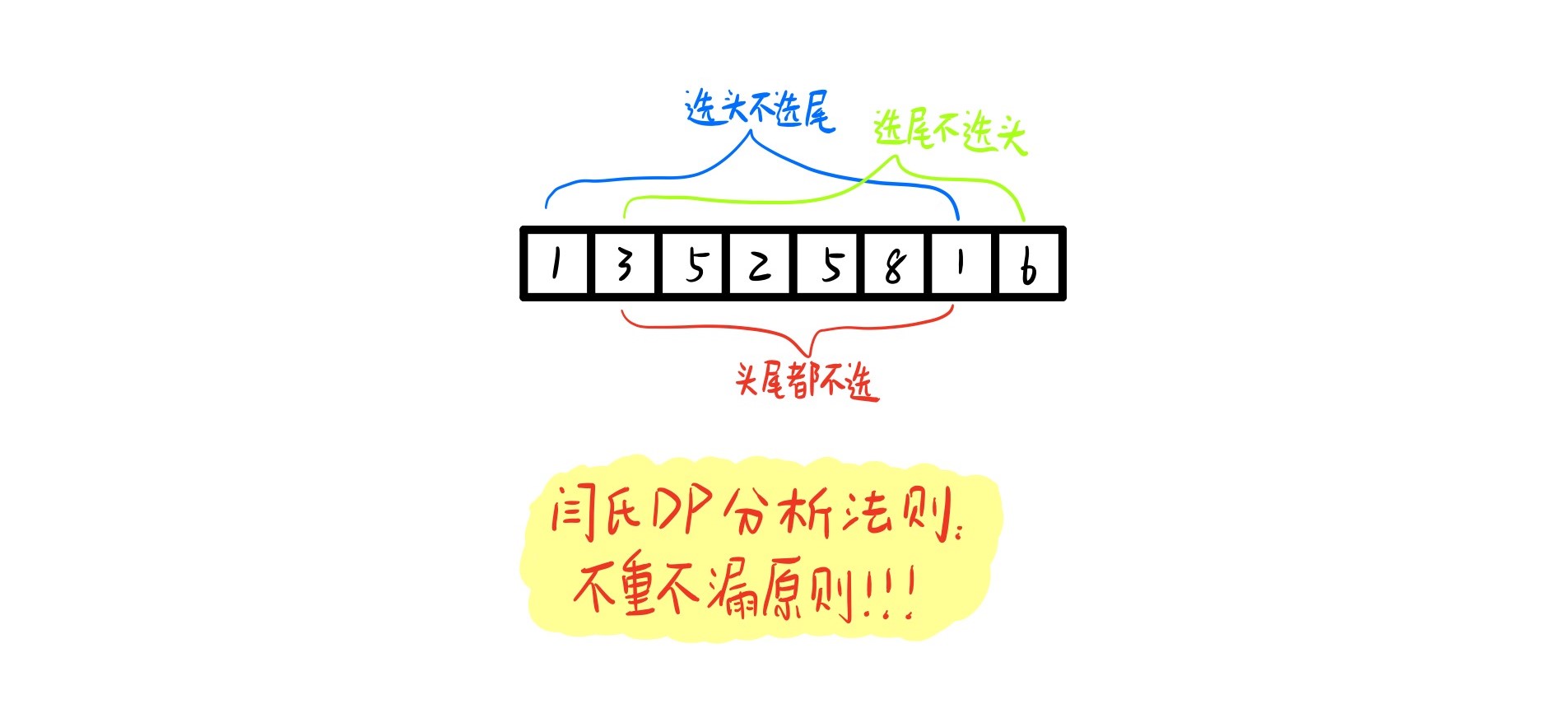
class Solution {
public int rob(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int n = nums.length;
if (n == 1) {
return nums[0];
}
// 前 i 家户可偷窃收益的最大值
int[] dp = new int[n];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for (int i = 2; i < n; i++) {
// 偷窃或不偷取 i 号房子
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[n - 1];
}
}
Ⅱ、数字三角形

DFS记忆化搜索与DP实现
import java.util.Scanner;
public class Main {
static final int N = 110;
static int n;
static int[][] triangle = new int[N][N], st = new int[N][N], dp = new int[N][N];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
triangle[i][j] = sc.nextInt();
}
}
sc.close();
System.out.println(dp());
System.out.println(dfs(1, 1, 1, 1));
}
// DP:dp[i][j]表示 0~i 行的第 j 个数字累加的最大值
static int dp() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
// 状态转移方程
dp[i][j] = triangle[i][j] + Math.max(dp[i - 1][j], dp[i - 1][j - 1]);
}
}
if (n % 2 == 0)
return Math.max(dp[n][n / 2], dp[n][n / 2 + 1]);
else
return dp[n][n / 2 + 1];
}
// DFS记忆化搜索
static int dfs(int a, int b, int l, int r) {
// 到达最后一行
if (a == n) {
if (Math.abs(l - r) <= 1) {
return triangle[a][b];
}
return 0;
}
// 递归向下搜索
int leftValue = st[a + 1][b] == 0 ? dfs(a + 1, b, l + 1, r) : st[a + 1][b];
int rightValue = st[a + 1][b + 1] == 0 ? dfs(a + 1, b + 1, l, r + 1) : st[a + 1][b + 1];
st[a][b] = triangle[a][b] + Math.max(leftValue, rightValue);
return st[a][b];
}
}
Ⅲ、李白打酒

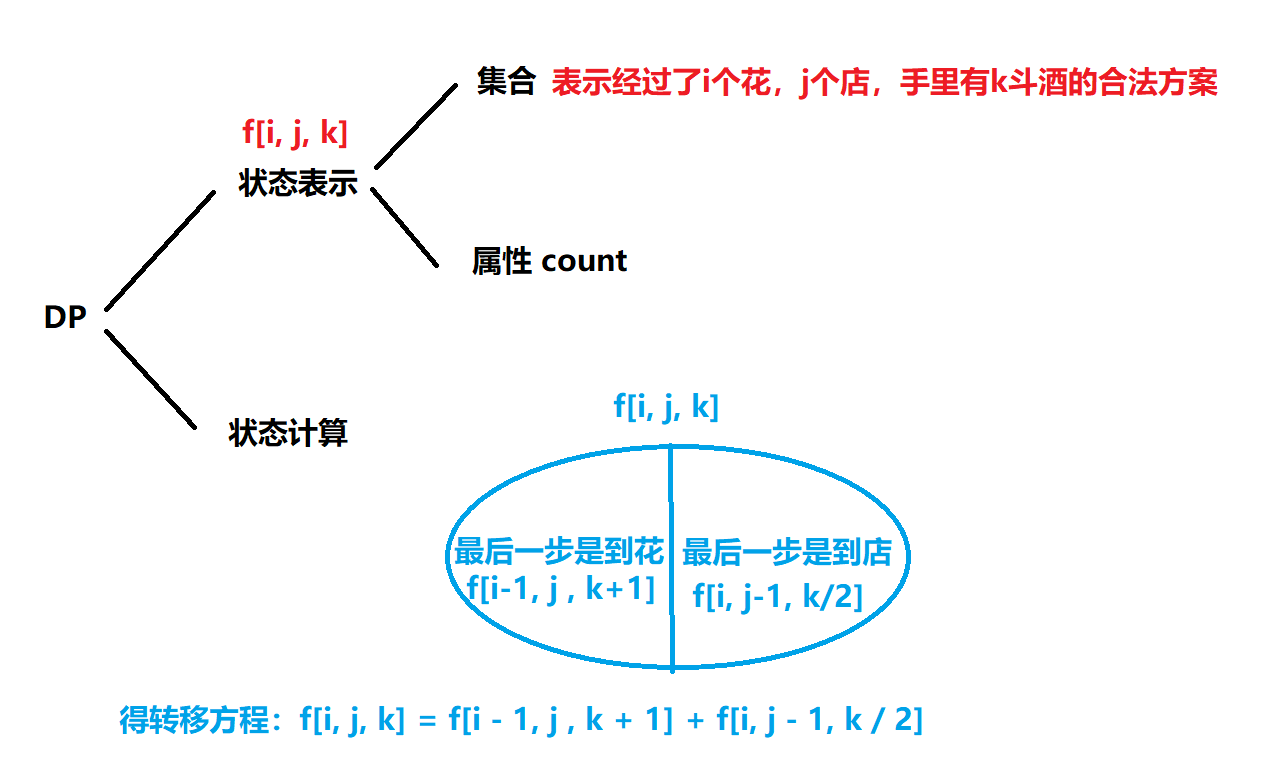
import java.util.Scanner;
public class Main {
static final int N = 110, MOD = 1000000007;
static int n, m;
static int[][][] dp = new int[N][N][N + 1]; // dp[i][j][k]表示路过了i家酒店,j朵花,还剩k斗酒的合法方案数
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
sc.close();
// 起始状态方案数为 1
dp[0][0][2] = 1;
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= m; j++) {
for (int k = 0; k < N; k++) {
// 当前方案数 + 最后一步遇到的是店的方案数
if (i > 0 && k % 2 == 0)
dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j][k / 2]) % MOD;
// 当前方案数 + 最后一步遇到的是花的方案数
if (j > 0)
dp[i][j][k] = (dp[i][j][k] + dp[i][j - 1][k + 1]) % MOD;
}
}
}
System.out.println(dp[n][m - 1][1]); // 输出最后一步为遇到花并剩1斗的方案数
}
}
三、状态压缩DP
状压DP复习参考:状态压缩DP学习总结+经典例题精解
Ⅰ、代码模板
// 总状态数
int maxn = 1 << n;
// 枚举已有的集合数:按照状态转移的顺序,一般从小编号到大编号
for(int i = 1; i <= m; ++ i){
// 枚举当前集合中的状态
for(int j = 0; j < maxn; ++ j){
// 判断当前集合是否处于合法状态
if(check(i, j)){
for(int k = 0; k < maxn; ++ k){
// 枚举上一个集合的状态
if(上一个集合的状态是否合格 + 上一个集合的状态和当前状态的集合是否产生了冲突){
// 列写状态转移方程
}
}
}
}
}
Ⅱ、最短Hamilton路径

闫式DP分析法
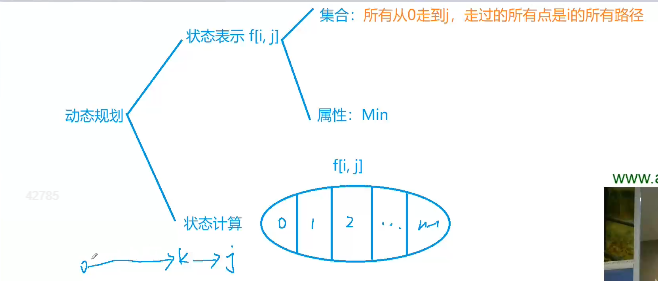
import java.util.*;
public class Main {
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), a[][] = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
a[i][j] = sc.nextInt();
}
}
sc.close();
// DP 状态表示:所有从0走到j,走过的所有点的情况是i的所有路径最小值
int dp[][] = new int[1 << n][n];
// 使用二进制状态压缩:走0,2,3这三个点表示为 11010;
for (int i = 0; i < (1 << n); i++) {
Arrays.fill(dp[i], (int) 1e9);
}
// 初始化旅行状态为 00001,停留在原点的值
dp[1][0] = 0;
for (int i = 2; i < (1 << n); i++) {
if (Integer.bitCount(i) != 1) {
for (int j = 0; j < n; j++) {
// 如果 i 的第 j 位为1,即本次状态路过了 j 点时
if ((i >> j & 1) == 1) {
// k 表示走到 j 这个点之前,以 k 为终点的最短距离
for (int k = 0; k < n; k++) {
if (j != k && (i >> k & 1) == 1) {
// 状态转移方程:f[i][j]=min(f[i][j], f[i-(1<<j)][k] + w[k][j])
dp[i][j] = Math.min(dp[i][j], dp[i ^ (1 << j)][k] + a[j][k]);
}
}
}
}
}
}
System.out.println(dp[(1 << n) - 1][n - 1]); // 表示所有点都走过了,,且终点是 n-1 的最短距离
}
}
四、背包DP
背包问题复习参考资料:14.4 0-1 背包问题 - Hello 算法
Ⅰ、代码模板
①01背包问题:
/* 0-1 背包:空间优化后的动态规划 */
int knapsackDPComp(int[] wgt, int[] val, int cap) {
int n = wgt.length;
// 初始化 dp 表
int[] dp = new int[cap + 1];
// 状态转移
for (int i = 1; i <= n; i++) {
// 倒序遍历
for (int c = cap; c >= 1; c--) {
if (wgt[i - 1] <= c) {
// 不选和选物品 i 这两种方案的较大值
dp[c] = Math.max(dp[c], dp[c - wgt[i - 1]] + val[i - 1]);
}
}
}
return dp[cap];
}
②完全背包问题:
/* 完全背包:空间优化后的动态规划 */
int unboundedKnapsackDPComp(int[] wgt, int[] val, int cap) {
int n = wgt.length;
// 初始化 dp 表
int[] dp = new int[cap + 1];
// 状态转移
for (int i = 1; i <= n; i++) {
for (int c = 1; c <= cap; c++) {
if (wgt[i - 1] > c) {
// 若超过背包容量,则不选物品 i
dp[c] = dp[c];
} else {
// 不选和选物品 i 这两种方案的较大值
dp[c] = Math.max(dp[c], dp[c - wgt[i - 1]] + val[i - 1]);
}
}
}
return dp[cap];
}
Ⅱ、货币系统

闫式DP分析法
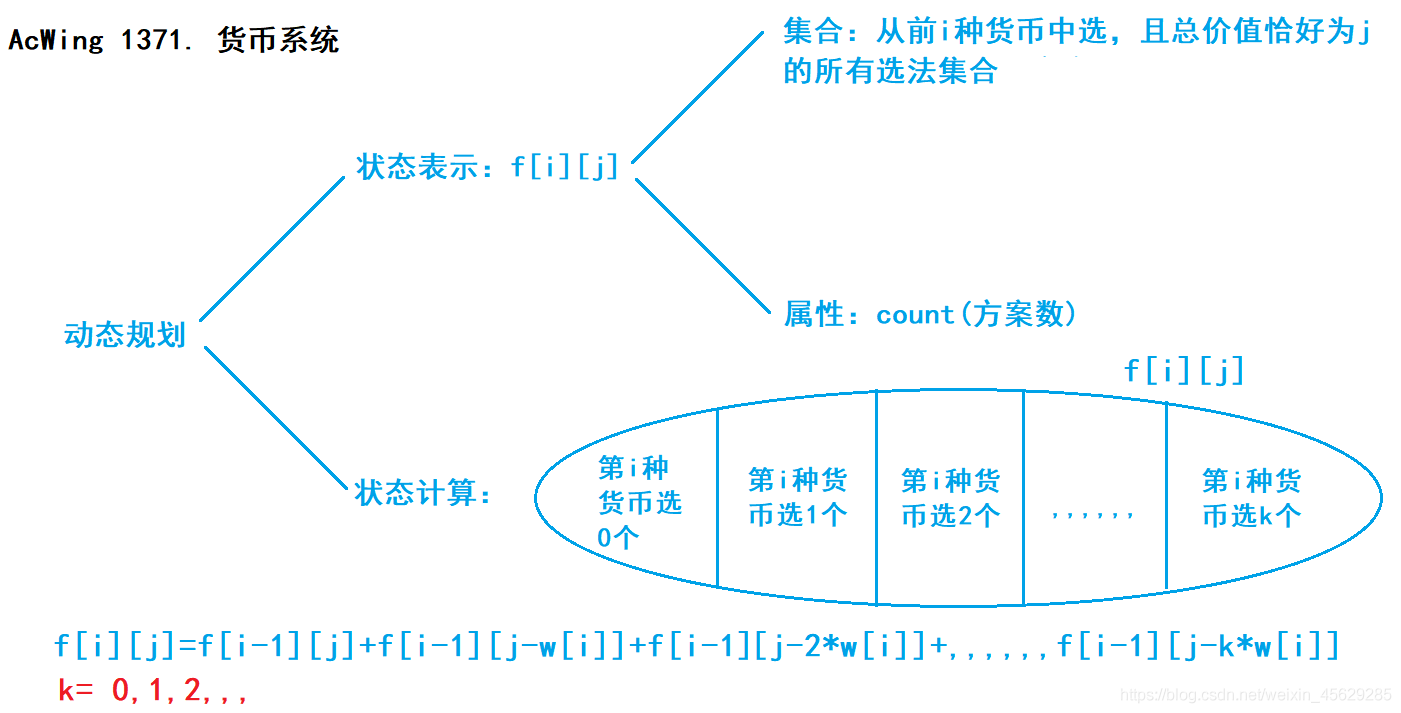
import java.util.Scanner;
public class Main {
static final int V = 30, N = 10010;
static int v, n;
static int[] coins = new int[V];
static long[][] dp = new long[V][N]; // dp[i][j]表示第 i 种硬币能凑出 j 金额的组合数最大值
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
n = sc.nextInt();
for (int i = 1; i <= v; i++) {
coins[i] = sc.nextInt();
}
sc.close();
dp[0][0] = 1;
for (int i = 1; i <= v; i++) {
for (int j = 0; j <= n; j++) {
for (int k = 0; k * coins[i] <= j; k++) {
dp[i][j] += dp[i - 1][j - k * coins[i]];
}
}
}
System.out.println(dp[v][n]);
}
}
Ⅲ、砝码称重

DP分析法
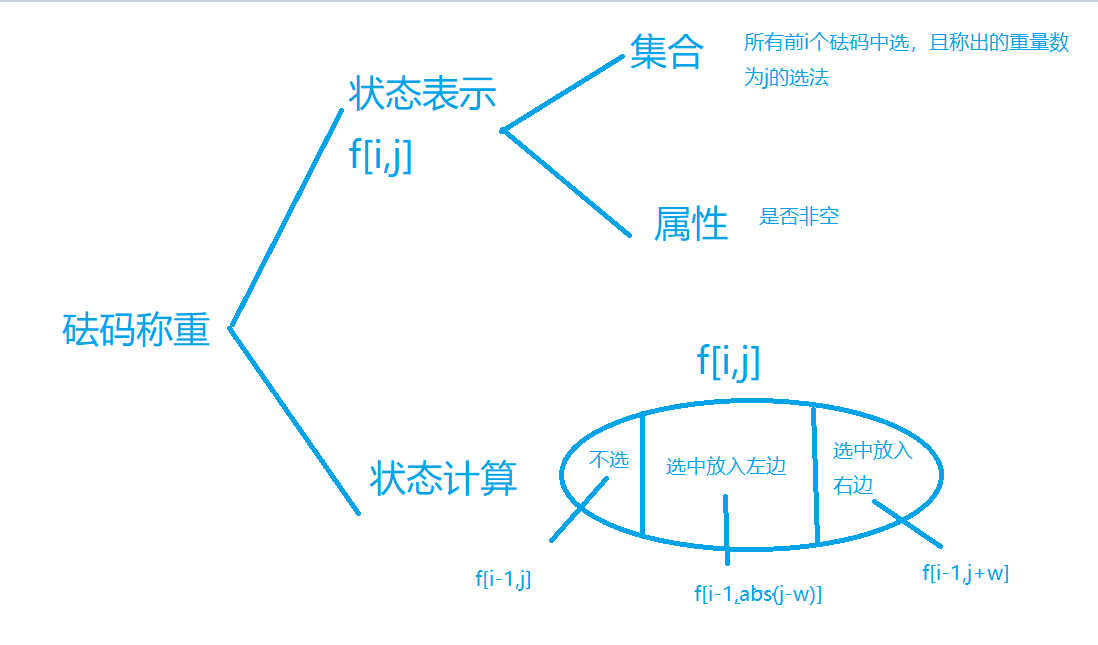
import java.util.Scanner;
public class Main {
static final int N = 110;
static int n, max = 0;
static int[] w = new int[N];
static boolean[][] dp = new boolean[N][200010]; // 前 i 个砝码可以称出重量 j 的布尔值
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
for (int i = 1; i <= n; i++) {
w[i] = sc.nextInt();
max += w[i];
}
sc.close();
dp[0][0] = true;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= max; j++) {
// 不选 || 选了放右边 || 选了放左边
dp[i][j] = dp[i - 1][j] || dp[i - 1][Math.abs(j - w[i])] || dp[i - 1][j + w[i]];
}
}
int res = 0;
for (int j = 1; j <= max; j++) {
if (dp[n][j])
res++;
}
System.out.println(res);
}
}
五、区间DP
区间DP算法博客参考:区间dp(含模板及例题)
Ⅰ、代码模板
for (int len = 1; len <= n; len++) { // 区间长度
for (int i = 1; i + len - 1 <= n; i++) { // 枚举起点
int j = i + len - 1; // 区间终点
if (len == 1) {
dp[i][j] = 初始值;
continue;
}
// 枚举分割点,构造状态转移方程
for (int k = i; k < j; k++) {
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
}
}
}
Ⅱ、石子合并

DP分析法
import java.io.*;
public class Main {
static final int N = 310;
static int n;
static int[] prefix = new int[N];
static int[][] dp = new int[N][N]; // dp[i][j]表示将区间[i, j]的石子合并成一堆的最小代价
/**
* 282. 石子合并(区间 DP 模版题详解)
*
* @param args
* @throws IOException
*/
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
String[] split = br.readLine().split("\\s+");
for (int i = 1; i <= n; i++) {
prefix[i] = Integer.parseInt(split[i - 1]);
prefix[i] += prefix[i - 1]; // 初始化前缀和数组
}
br.close();
// 枚举长度和左端点
for (int len = 2; len <= n; len++) {
for (int i = 1; i + len - 1 <= n; i++) {
int j = i + len - 1; // 计算右端点
dp[i][j] = Integer.MAX_VALUE;
// 枚举边界分界点
for (int k = i; k < j; k++) {
// min(dp[i][j], 合并左侧的最小代价 + 合并右侧的最小代价 + 合并两侧的代价(区间和))
dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k + 1][j] + prefix[j] - prefix[i - 1]);
}
}
}
System.out.println(dp[1][n]); // 区间[1, n]合并的最小代价
}
}
六、树形DP
算法资料参考:算法与数据结构——树形dp套路(java)
Ⅰ、邻接表模板
在解决树形DP问题时,需要先将树形结构用邻接表表示出来。
初始化邻接表
// head[x] = m 表示点 x 的邻接表的表头是编号为 m 的边
// ver[m] 表示编号为 m 的边的终点
// edge[m] 表示编号为 m 的边的权值
// next[m] 表示编号为 m 的边的下一个节点
static int head[N], ver[M], edge[M], next[M], idx;
// 初始化head
Arrays.fill(head, -1);
// 加入有向边 (x, y),权值为 z
static void add(int x, int y, int z) {
// 真实数据
ver[idx] = y;
edge[idx] = z;
// 在表头 x 处插入
next[idx] = head[x];
head[x] = idx++;
}
访问从 x 出发的所有边
for (int i = head[x]; i != -1; i = next[i]) {
// 找到了一条有向边 (x, y),权值为 z
int y = ver[i], z = edge[i];
}
有向图和无向图区别在于,将一条边 (u, v, w) 看成 (u, v, w) 和 (v, u, w) 两条边调用 add 加入邻接表。
Ⅱ、没有上司的舞会

DP分析
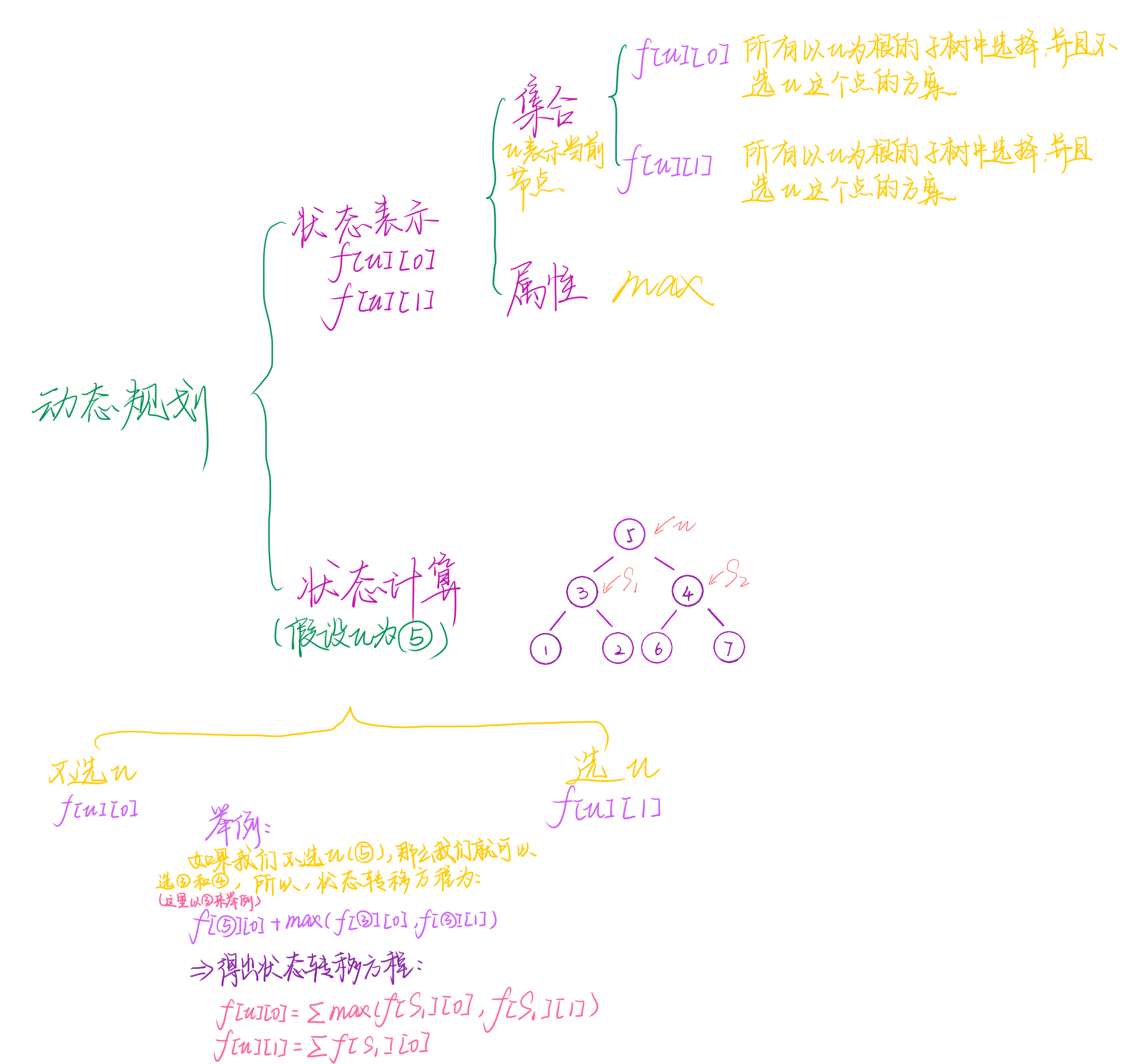
import java.util.*;
public class Main {
static final int N = 6010;
static int n;
static int[] h = new int[N];
static Map<Integer, List<Integer>> map = new HashMap<>();
static int[][] dp = new int[N][2]; // dp[x][2] 表示选 x 这颗子树且选或不选 x 节点本身的最大快乐指数
static boolean st[] = new boolean[N]; // st[i] 表示节点 i 是否有父节点
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
for (int i = 1; i <= n; i++) {
h[i] = sc.nextInt();
}
for (int i = 0; i < n - 1; i++) {
int l = sc.nextInt();
int k = sc.nextInt();
st[l] = true;
add(k, l);
}
sc.close();
// 初始化dp
for (int i = 1; i <= n; i++) {
dp[i][1] = h[i];
}
// 查找根节点
int root = 0;
for (int i = 1; i <= n; i++) {
if (!st[i]) {
root = i;
break;
}
}
// 递归计算树形DP值
dfs(root);
System.out.println(Math.max(dp[root][0], dp[root][1]));
}
// 递归遍历树结构计算DP
static void dfs(int x) {
List<Integer> list = map.get(x);
if (list == null)
return;
// 遍历子节点
for (int son : list) {
dfs(son);
dp[x][1] += dp[son][0]; // 选择 x 节点及其子树:累加所有子节点但不选自身的最大指数
dp[x][0] += Math.max(dp[son][1], dp[son][0]); // 选择子树但不选择 x 自身:累加所有子节点选或不选自身的较大值
}
}
// 通过map构造树结构
static void add(int a, int b) {
if (!map.containsKey(a))
map.put(a, new ArrayList<>());
map.get(a).add(b);
}
}
Ⅲ、病毒溯源

import java.util.*;
public class Main {
static final int N = 10010;
static int n, idx;
static int[] son = new int[N], st = new int[N];
static int[] edge = new int[N], ver = new int[N], next = new int[N], head = new int[N]; // 邻接表
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
Arrays.fill(head, -1);
Arrays.fill(son, -1);
for (int i = 0; i < n; i++) {
int m = sc.nextInt();
while (m-- > 0) {
int x = sc.nextInt();
add(i, x, x);
st[x] = 1;
}
}
sc.close();
// 寻找根节点
int root = 0;
for (int i = 0; i < n; i++) {
if (st[i] != 1) {
root = i;
break;
}
}
// DFS搜索
System.out.println(dfs(root));
System.out.print(root);
while (son[root] != -1) {
root = son[root];
System.out.print(" " + root);
}
}
// DFS遍历树结构
public static int dfs(int x) {
int res = 0;
for (int i = head[x]; i != -1; i = next[i]) {
int j = ver[i];
int d = dfs(j);
// 更新最长路径值
if (d > res || (d == res && j < son[x])) {
res = d;
son[x] = j; // 通过存储下标更新路径
}
}
return res + 1;
}
// 邻接表存储树结构
public static void add(int a, int b, int w) {
ver[idx] = b;
edge[idx] = w;
next[idx] = head[a];
head[a] = idx++;
}
}
