布林带
SharpCharts 计算
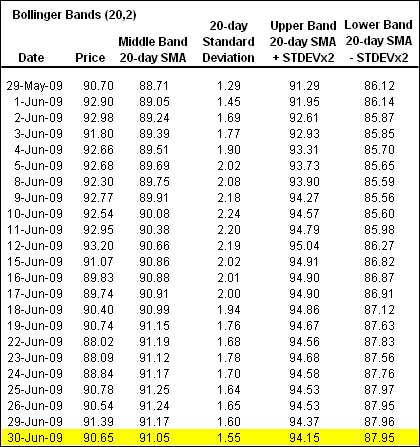
* Middle Band = 20-day simple moving average (SMA)
* Upper Band = 20-day SMA + (20-day standard deviation of price x 2)
* Lower Band = 20-day SMA - (20-day standard deviation of price x 2)
点击这里下载此电子表格示例。")
布林带由一个中间带和两个外部带组成。 中间带是一个通常设置为 20 个周期的简单移动平均。使用简单移动平均是因为标准差公式也使用简单移动平均。标准差的回溯期与简单移动平均相同。外部带通常设置在中间带的上下 2 个标准差处。
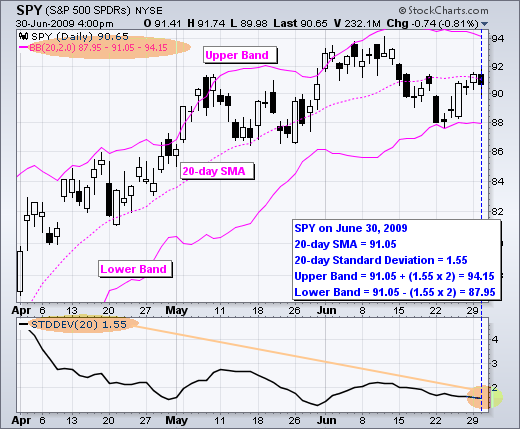
设置可以调整以适应特定证券或交易风格的特征。 布林格建议对标准差乘数进行小幅调整。 更改移动平均线的周期数也会影响用于计算标准差的周期数。 因此,标准差乘数只需要进行小幅调整。 增加移动平均线周期将自动增加用于计算标准差的周期数,并且还需要增加标准差乘数。 使用 20 天 SMA 和 20 天标准差,标准差乘数设置为 2。 布林格建议将标准差乘数增加到 2.1 以用于 50 周期 SMA,并将标准差乘数降低到 1.9 以用于 10 周期 SMA。
代码
名称:布林带计算
描述:根据给定的DataFrame计算布林带指标
代码:
def bollinger_bands(df):
df['Middle Band'] = df['close'].rolling(window=20).mean()
df['Upper Band'] = df['Middle Band'] + (df['close'].rolling(window=20).std() * 2)
df['Lower Band'] = df['Middle Band'] - (df['close'].rolling(window=20).std() * 2)
return df
吊灯退出
计算
吊灯退出公式由三部分组成:周期高点或周期低点、平均真实范围(ATR)和一个乘数。在日线图上使用默认设置的 22 周期,吊灯退出将寻找过去 22 天的最高点或最低点。请注意,一个月有 22 个交易日。这个参数(22)也将用于计算平均真实范围。
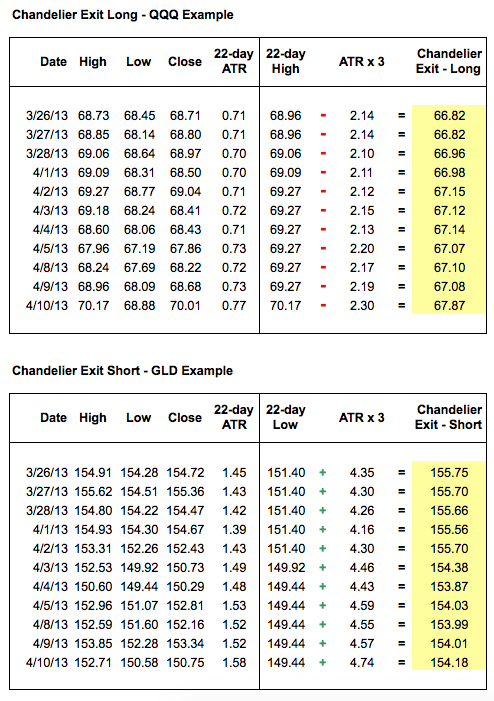
Chandelier Exit (long) = 22-day High - ATR(22) x 3
Chandelier Exit (short) = 22-day Low + ATR(22) x 3
如上述公式所示,长仓和短仓都有一个吊灯退出。吊灯退出(长仓)悬挂在 22 周期高点的三个 ATR 值以下。这意味着随着周期高点和 ATR 值的变化,它会上升和下降。短仓的吊灯退出放置在 22 周期低点的三个 ATR 值以上。电子表格示例展示了两者的样本计算。
代码
# 计算吊灯退出指标
def chandelier_exit(df):
# 计算 ATR
df['TR'] = df['high'] - df['low']
df['TR1'] = abs(df['high'] - df['close'].shift())
df['TR2'] = abs(df['low'] - df['close'].shift())
df['TR'] = df[['TR', 'TR1', 'TR2']].max(axis=1)
df['ATR'] = df['TR'].rolling(window=22).mean()
# 计算吊灯退出(长仓和短仓)
df['Chandelier_Exit_Long'] = df['high'].rolling(window=22).max() - df['ATR'] * 3
df['Chandelier_Exit_Short'] = df['low'].rolling(window=22).min() + df['ATR'] * 3
return df[['Chandelier_Exit_Long', 'Chandelier_Exit_Short']]
# 使用示例
result = chandelier_exit(df)
print(result)
一目均衡云
计算
一目均衡云中的五个图表中的四个是基于一定时间内的高低平均值。例如,第一个图表只是 9 天高点和 9 天低点的平均值。在计算机普及之前,计算这种高低平均值可能比计算 9 天移动平均线更容易。一目均衡云由五个图表组成:
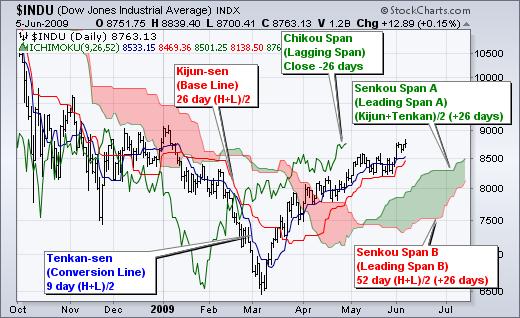
Tenkan-sen (Conversion Line): (9-period high + 9-period low)/2))
The default setting is 9 periods and can be adjusted. On a daily chart, this line is the midpoint of the 9-day high-low range,
which is almost two weeks.
Kijun-sen (Base Line): (26-period high + 26-period low)/2))
The default setting is 26 periods and can be adjusted. On a daily chart, this line is the midpoint of the 26-day high-low range, which is almost one month).
Senkou Span A (Leading Span A): (Conversion Line + Base Line)/2))
This is the midpoint between the Conversion Line and the Base Line. The Leading Span A forms one of the two Cloud boundaries. It is referred to as "Leading" because it is plotted 26 periods in the future and forms the faster Cloud boundary.
Senkou Span B (Leading Span B): (52-period high + 52-period low)/2))
On the daily chart, this line is the midpoint of the 52-day high-low range, which is a little less than 3 months. The default calculation setting is 52 periods, but can be adjusted. This value is plotted 26 periods in the future and forms the slower Cloud boundary.
Chikou Span (Lagging Span): Close plotted 26 days in the past
The default setting is 26 periods, but can be adjusted.
本教程在解释各种图表时将使用英文等效词。下表显示了道琼斯工业指数与一目均衡云图的情况。转换线(蓝色)是最快、最敏感的线。请注意,它最接近价格走势。基准线(红色)落后于更快的转换线,但在很大程度上跟随价格走势。转换线和基准线之间的关系类似于 9 日移动平均线和 26 日移动平均线之间的关系。9 日线更快,更紧密地跟随价格走势。26 日线较慢,落后于 9 日线。顺便提一下,注意到 9 和 26 是用来计算 MACD 的相同周期。
代码
名称:一目均衡云计算
描述:根据给定的开盘价、最高价、最低价和收盘价计算一目均衡云中的各个指标
代码:
def calculate_ichimoku_cloud(df):
# Tenkan-sen (Conversion Line)
nine_period_high = df['high'].rolling(window=9).max()
nine_period_low = df['low'].rolling(window=9).min()
df['tenkan_sen'] = (nine_period_high + nine_period_low) / 2
# Kijun-sen (Base Line)
twenty_six_period_high = df['high'].rolling(window=26).max()
twenty_six_period_low = df['low'].rolling(window=26).min()
df['kijun_sen'] = (twenty_six_period_high + twenty_six_period_low) / 2
# Senkou Span A (Leading Span A)
df['senkou_span_a'] = ((df['tenkan_sen'] + df['kijun_sen']) / 2).shift(26)
# Senkou Span B (Leading Span B)
fifty_two_period_high = df['high'].rolling(window=52).max()
fifty_two_period_low = df['low'].rolling(window=52).min()
df['senkou_span_b'] = ((fifty_two_period_high + fifty_two_period_low) / 2).shift(26)
# Chikou Span (Lagging Span)
df['chikou_span'] = df['close'].shift(-26)
return df
考夫曼自适应移动平均线(KAMA)
计算
计算考夫曼自适应移动平均线需要几个步骤。让我们首先从佩里·考夫曼推荐的设置开始:KAMA(10,2,30)。
-
10 是效率比率(ER)的周期数。
-
2 是最快 EMA 常数的周期数。
-
30 是最慢 EMA 常数的周期数。
在计算 KAMA 之前,我们需要计算效率比率(ER)和平滑常数(SC)。将公式分解成易于理解的小块有助于理解指标背后的方法论。请注意,ABS 代表绝对值。
代码
## 计算
名称:{KAMA}
描述:计算考夫曼自适应移动平均线(KAMA)
--- 代码:
def KAMA(df):
er_window = 10
fast_period = 2
slow_period = 30
df['change'] = df['close'] - df['close'].shift(1)
df['volatility'] = abs(df['close'] - df['close'].shift(er_window))
df['er'] = df['change'] / df['volatility']
sc_fast = 2 / (fast_period + 1)
sc_slow = 2 / (slow_period + 1)
df['sc'] = (df['er'] * (sc_fast - sc_slow) + sc_slow) ** 2
df['kama'] = 0.0
for i in range(er_window, len(df)):
if df['kama'][i-1] != 0:
df['kama'][i] = df['kama'][i-1] + df['sc'][i] * (df['close'][i] - df['kama'][i-1])
else:
df['kama'][i] = df['close'][i]
return df['kama']
凯尔特纳通道
计算
计算凯尔特纳通道有三个步骤。首先,选择指数移动平均线的长度。其次,选择真实波幅(ATR)的时间周期。第三,选择真实波幅的乘数。
Middle Line: 20-day exponential moving average
Upper Channel Line: 20-day EMA + (2 x ATR(10))
Lower Channel Line: 20-day EMA - (2 x ATR(10))
上面的示例基于 SharpCharts 的默认设置。由于移动平均线滞后于价格,较长的移动平均线会有更多的滞后,而较短的移动平均线则会有较少的滞后。ATR 是基本的波动率设置。较短的时间框架,如 10,会产生更加波动的 ATR,随着 10 期波动性的起伏而波动。较长的时间框架,如 100,会平滑这些波动,产生更加稳定的 ATR 读数。乘数对通道宽度影响最大。简单地从 2 改为 1 会将通道宽度减半。从 2 增加到 3 会使通道宽度增加 50%。
这里有一张图表展示了三条 Keltner 通道,分别设置在中心移动平均线的 1、2 和 3 个 ATR 之外。这种特定技术多年来一直由 SpikeTrade.com 的 Kerry Lovvorn 提倡。
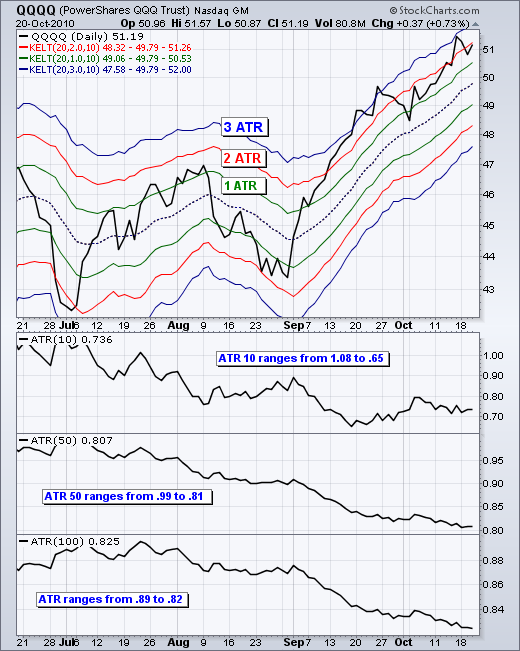
上图显示了默认的红色 Keltner 通道,更宽的蓝色通道和更窄的绿色通道。蓝色通道设置为中心移动平均线的三个平均真实范围值之上和之下(3 x ATR)。绿色通道使用一个 ATR 值。所有三个通道共享 20 天的 EMA,即中间的虚线。指标窗口显示了 10 期、50 期和 100 期的平均真实范围(ATR)的差异。请注意,短期 ATR(10)更加波动,范围更广。相比之下,100 期 ATR 更加平稳,范围波动较小。
代码
名称:Keltner通道
描述:根据给定的参数计算Keltner通道的三条线
def keltner_channel(df, ema_length=20, atr_length=10, multiplier=2):
df['EMA'] = df['close'].ewm(span=ema_length, adjust=False).mean()
df['ATR'] = df['high'].rolling(window=atr_length).max() - df['low'].rolling(window=atr_length).min()
df['Upper_Channel'] = df['EMA'] + (multiplier * df['ATR'])
df['Lower_Channel'] = df['EMA'] - (multiplier * df['ATR'])
return df[['EMA', 'Upper_Channel', 'Lower_Channel']]
移动平均线 - 简单和指数
简单移动平均线计算
简单移动平均线是通过计算特定周期内某个证券的平均价格形成的。 大多数移动平均线是基于收盘价格的。 5 天简单移动平均线是收盘价格的五天总和除以五。 正如其名称所示,移动平均线是一个移动的平均值。 随着新数据的出现,旧数据被丢弃。 这导致平均值沿着时间尺度移动。 以下是一个 5 天移动平均线在三天内演变的示例。
Daily Closing Prices: 11,12,13,14,15,16,17
First day of 5-day SMA: (11 + 12 + 13 + 14 + 15) / 5 = 13
Second day of 5-day SMA: (12 + 13 + 14 + 15 + 16) / 5 = 14
Third day of 5-day SMA: (13 + 14 + 15 + 16 + 17) / 5 = 15
移动平均线的第一天简单地涵盖了过去五天。 移动平均线的第二天删除了第一个数据点(11)并添加了新的数据点(16)。 移动平均线的第三天继续删除第一个数据点(12)并添加新的数据点(17)。 在上面的示例中,价格在七天内逐渐从 11 增加到 17。 请注意,移动平均线在三天的计算期间也从 13 上升到 15。 还要注意,每个移动平均值都略低于最后的价格。 例如,第一天的移动平均值等于 13,而最后的价格是 15。 过去四天的价格较低,这导致移动平均线滞后。
代码
名称:simple_moving_average
描述:计算简单移动平均线
---
代码:
def simple_moving_average(df, window):
df['SMA'] = df['close'].rolling(window=window).mean()
return df
移动平均包络
计算
移动平均包络的计算方法很简单。首先,选择简单移动平均或指数移动平均。简单移动平均对每个数据点(价格)的权重相同。指数移动平均对最近的价格赋予更大的权重,滞后性更小。其次,选择移动平均的时间周期数。第三,设置包络的百分比。一个 20 天的移动平均线,带有 2.5%的包络,将显示以下两条线:
Upper Envelope: 20-day SMA + (20-day SMA x .025)
Lower Envelope: 20-day SMA - (20-day SMA x .025)
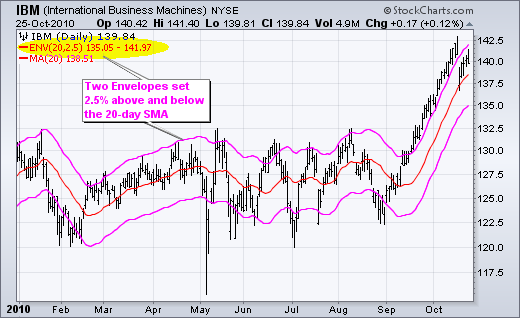
上图显示了 IBM 的 20 天简单移动平均线和 2.5%的包络。请注意,20 天简单移动平均线被添加到此 SharpChart 中以供参考。请注意包络如何与 20 天简单移动平均线平行移动。它们始终保持在移动平均线的上方和下方的恒定 2.5%。
代码
名称:移动平均包络
描述:根据给定的DataFrame计算移动平均包络
代码:
def moving_average_envelope(df, window=20, percentage=0.025):
df['SMA'] = df['close'].rolling(window=window).mean()
df['Upper Envelope'] = df['SMA'] + (df['SMA'] * percentage)
df['Lower Envelope'] = df['SMA'] - (df['SMA'] * percentage)
return df[['SMA', 'Upper Envelope', 'Lower Envelope']]
抛物线 SAR
计算
SAR 的计算涉及复杂的 if/then 变量,使其难以放入电子表格中。这些示例将提供 SAR 计算的一般概念。由于上升 SAR 和下降 SAR 的公式不同,因此更容易将计算分为两部分。第一部分涵盖上升 SAR 的计算,第二部分涵盖下降 SAR。
Rising SAR
----------
Prior SAR: The SAR value for the previous period.
Extreme Point (EP): The highest high of the current uptrend.
Acceleration Factor (AF): Starting at .02, AF increases by .02 each time the extreme point makes a new high. AF can reach a maximum of .20, no matter how long the uptrend extends.
Current SAR = Prior SAR + Prior AF(Prior EP - Prior SAR)
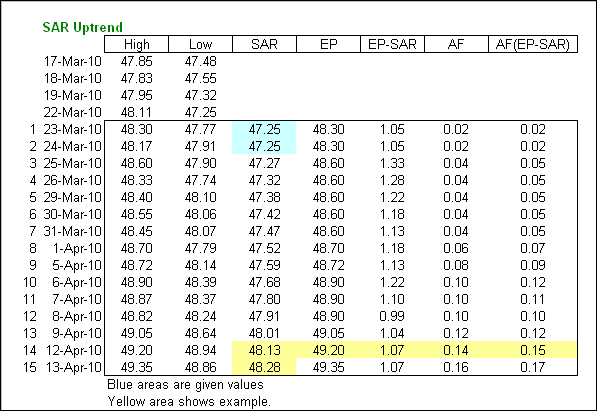
13-Apr-10 SAR = 48.28 = 48.13 + .14(49.20 - 48.13)
The Acceleration Factor is multiplied by the difference between the Extreme Point and the prior period's SAR. This is then added to the prior period's SAR. Note however that SAR can never be above the prior two periods' lows. Should SAR be above one of those lows, use the lowest of the two for SAR.
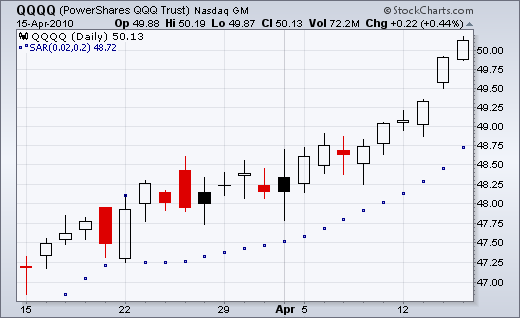
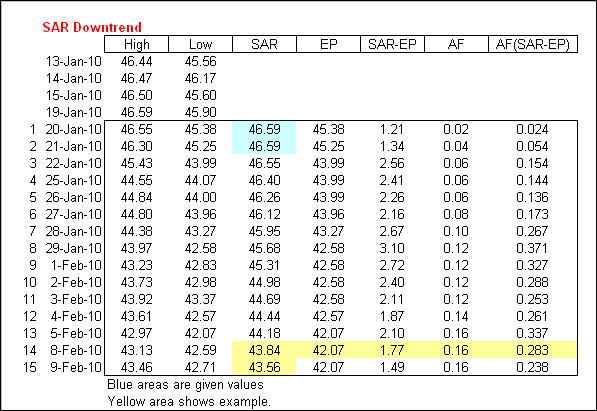
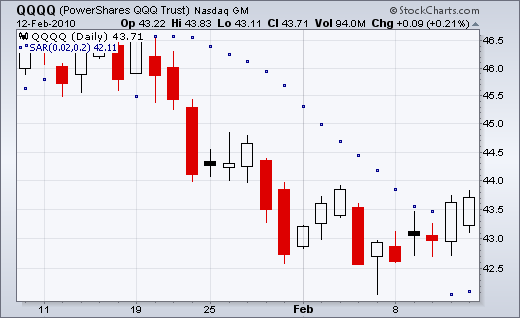
Falling SAR
-----------
Prior SAR: The SAR value for the previous period.
Extreme Point (EP): The lowest low of the current downtrend.
Acceleration Factor (AF): Starting at .02, AF increases by .02 each time the extreme point makes a new low. AF can reach a maximum of .20, no matter how long the downtrend extends.
Current SAR = Prior SAR - Prior AF(Prior SAR - Prior EP)
9-Feb-10 SAR = 43.56 = 43.84 - .16(43.84 - 42.07)
The Acceleration Factor is multiplied by the difference between the Prior period's SAR and the Extreme Point. This is then subtracted from the prior period's SAR. Note however that SAR can never be below the prior two periods' highs. Should SAR be below one of those highs, use the highest of the two for SAR.
代码
名称:SAR计算
描述:根据给定的开盘价、最高价、最低价和收盘价计算抛物线 SAR 指标
import pandas as pd
def calculate_SAR(df):
df['SAR'] = 0
df['AF'] = 0
df['EP'] = 0
for i in range(2, len(df)):
if df['high'][i-1] > df['high'][i-2] and df['low'][i-1] > df['low'][i-2]:
df.at[i, 'AF'] = min(df['AF'][i-1] + 0.02, 0.2)
elif df['high'][i-1] < df['high'][i-2] and df['low'][i-1] < df['low'][i-2]:
df.at[i, 'AF'] = max(df['AF'][i-1] - 0.02, 0.02)
else:
df.at[i, 'AF'] = df['AF'][i-1]
if df['AF'][i] == 0.2:
df.at[i, 'EP'] = df['high'][i]
else:
df.at[i, 'EP'] = df['EP'][i-1]
if df['AF'][i] > 0:
if df['AF'][i-1] > 0:
if df['high'][i] > df['EP'][i-1]:
df.at[i, 'SAR'] = df['SAR'][i-1] + df['AF'][i-1] * (df['EP'][i-1] - df['SAR'][i-1])
else:
df.at[i, 'SAR'] = df['EP'][i-1]
else:
df.at[i, 'SAR'] = df['EP'][i-1]
else:
if df['AF'][i-1] < 0:
if df['low'][i] < df['EP'][i-1]:
df.at[i, 'SAR'] = df['SAR'][i-1] - df['AF'][i-1] * (df['SAR'][i-1] - df['EP'][i-1])
else:
df.at[i, 'SAR'] = df['EP'][i-1]
else:
df.at[i, 'SAR'] = df['EP'][i-1]
return df
# 使用示例
df = pd.DataFrame({
'open': [50, 48, 47, 45, 46],
'high': [52, 50, 49, 48, 47],
'low': [48, 46, 45, 43, 44],
'close': [49, 47, 46, 44, 45]
})
df = calculate_SAR(df)
print(df)
枢轴点
代码
名称:{title}
描述:计算股票的收益率
---
代码:
def calculate_returns(df):
df['returns'] = df['close'].pct_change()
return df
价格通道
计算
Upper Channel Line: 20-day high
Lower Channel Line: 20-day low
Centerline: (20-day high + 20-day low)/2
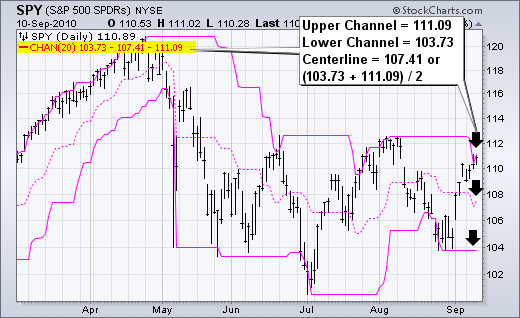
上述公式基于日线图和 20 周期价格通道,这是 SharpCharts 中的默认设置。价格通道可用于分钟线、日线、周线或月线图表。回溯期(20)可以更短或更长。较短的回溯期,如 10 天,产生更紧密的通道线。较长的回溯期产生更宽的通道。
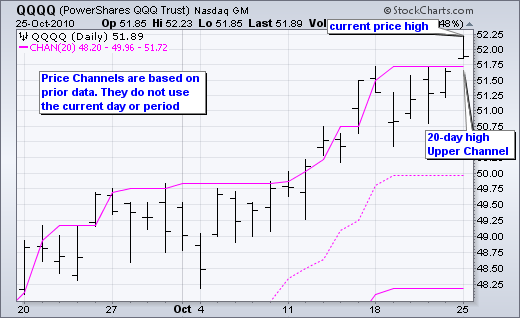
价格通道公式不包括最近的周期。价格通道是基于当前周期之前的价格。10 月 21 日的 20 天价格通道将基于前一天 10 月 20 日的 20 天高点和 20 天低点。如果使用最近的周期,通道突破将不可能发生。在下面的图表中,请注意价格如何突破了上方价格通道,因为高点是基于倒数第二根柱子,而不是当前柱子。
代码
# 计算价格通道指标
def calculate_price_channel(df):
df['Upper Channel Line'] = df['high'].rolling(window=20).max()
df['Lower Channel Line'] = df['low'].rolling(window=20).min()
df['Centerline'] = (df['Upper Channel Line'] + df['Lower Channel Line']) / 2
return df
成交量价格
计算
成交量价格计算基于图表上显示的整个时期。五个月日线图上的成交量价格是基于所有五个月的每日收盘数据。两周 30 分钟图上的成交量价格是基于两周的 30 分钟收盘数据。三年周线图上的成交量价格是基于三年的每周收盘数据。你明白了吧。成交量价格计算不会超出图表显示的历史数据范围。
There are four steps involved in the calculation.
This example is based on closing prices and the default parameter setting (12).
1\. Find the high-low range for closing prices for the entire period.
2\. Divide this range by 12 to create 12 equal price zones.
3\. Total the amount of volume traded within each price zone.
4\. Divide the volume into up volume and down volume (optional).
请注意,当收盘价格从一个周期下跌到下一个周期时,成交量为负。当收盘价格从一个周期上涨到下一个周期时,成交量为正。
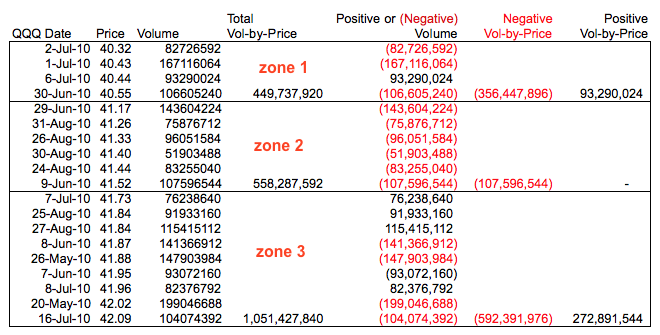
上面的示例显示了从 2010 年 4 月 12 日到 9 月 15 日对纳斯达克 100ETF 进行的成交量价格计算。在此期间,收盘价格范围从 40.32 到 47.87(47.87 - 40.32 = 7.55)。一百一十个收盘价格(每个交易日一个)从低到高排序,然后分成 12 个均匀的价格区间(7.55/12 = .6292)。
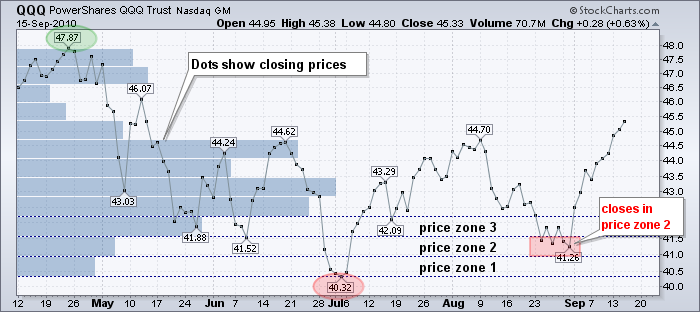
上图突出显示了前三个价格区间(40.32 至 40.95,40.96 至 41.58 和 41.59 至 42.21)。从低点(40.32)开始,我们可以添加区间大小(.6292)以创建导致高点的价格区间。只有落在这些区间内的价格才用于特定的成交量价格计算。
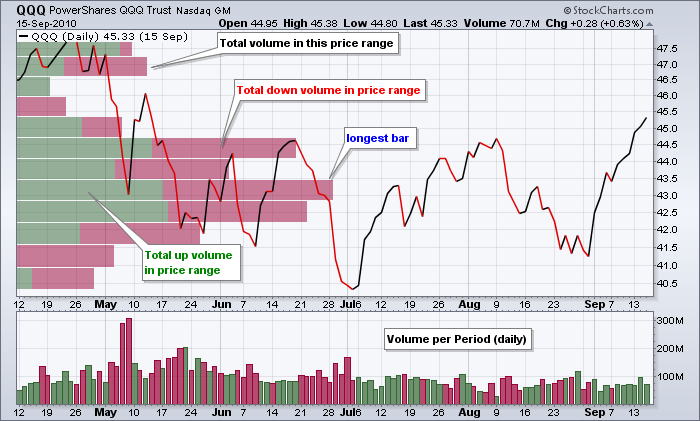
成交量价格条代表每个价格区间的总成交量。成交量可以分为正成交量和负成交量。请注意上图中的成交量价格条是红色和绿色的,以区分正成交量和负成交量。
代码
名称:成交量价格计算
描述:根据给定的收盘价和成交量数据,计算成交量价格
代码:
def calculate_volume_price(df):
# Step 1: Find the high-low range for closing prices for the entire period
price_range = df['close'].max() - df['close'].min()
# Step 2: Divide the range by 12 to create 12 equal price zones
price_zone = price_range / 12
# Step 3: Total the amount of volume traded within each price zone
df['price_zone'] = ((df['close'] - df['close'].min()) // price_zone).astype(int)
volume_price = df.groupby('price_zone')['volume'].sum()
# Step 4: Divide the volume into up volume and down volume
df['volume_direction'] = df['close'].diff().apply(lambda x: 1 if x > 0 else -1)
up_volume = df[df['volume_direction'] == 1].groupby('price_zone')['volume'].sum()
down_volume = df[df['volume_direction'] == -1].groupby('price_zone')['volume'].sum()
return volume_price, up_volume, down_volume
成交量加权平均价格(VWAP)
计算
VWAP 计算涉及五个步骤。首先,计算日内周期的典型价格。这是高、低和收盘价的平均值:{(H+L+C)/3)}。其次,将典型价格乘以周期的成交量。第三,创建这些值的累积总和。这也被称为累积总和。第四,创建成交量的累积总和(累积成交量)。第五,将价格-成交量的累积总和除以成交量的累积总和。
Cumulative(Volume x Typical Price)/Cumulative(Volume)

上面的示例显示了 IBM 交易的前 30 分钟的 1 分钟 VWAP。通过将累积价格-成交量除以累积成交量,产生一个根据成交量调整(加权)的价格水平。第一个 VWAP 值始终是典型价格,因为分子和分母中的成交量相等。它们在第一次计算中互相抵消。下图显示了 IBM 的 1 分钟 K 线图和 VWAP。在交易的前 30 分钟内,价格从最高的 127.36 到最低的 126.67。实际上,前 30 分钟非常波动。VWAP 的范围从 127.21 到 127.09,并且大部分时间处于这个范围的中间。

代码
名称:VWAP
描述:计算成交量加权平均价格
def vwap(df):
typical_price = (df['high'] + df['low'] + df['close']) / 3
cumulative_price_volume = (typical_price * df['volume']).cumsum()
cumulative_volume = df['volume'].cumsum()
vwap = cumulative_price_volume / cumulative_volume
return vwap
ZigZag
计算
ZigZag 基于图表的“类型”。基于收盘价的线状和点状图表将显示基于收盘价的 ZigZag。高低收盘价柱状图(HLC)、开盘-最高-最低-收盘价柱状图(OHLC)和蜡烛图显示了周期的高低范围,将显示基于这一高低范围的 ZigZag。基于高低范围的 ZigZag 更有可能改变方向,因为高低范围会更大,产生更大的波动。
参数框允许图表分析者设置 ZigZag 功能的灵敏度。参数框中设置为 5 的 ZigZag 将过滤掉所有小于 5%的波动。设置为 10 的 ZigZag 将过滤掉小于 10%的波动。如果一支股票从 100 的反弹低点到 109 的高点(+9%),则不会有线条,因为波动小于 10%。如果股票从 100 的低点上涨到 110 的高点(+10%),则会有一条线从 100 到 110。如果股票继续上涨到 112,这条线将延伸到 112(从 100 到 112)。直到股票从高点下跌 10%或更多,ZigZag 才会反转。从 112 的高点开始,股票必须下跌 11.2 点(或至 100.8 的低点)才能再次出现线条。下面的图表显示了一个带有 7% ZigZag 的 QQQQ 线状图。6 月初的反弹被忽略,因为小于 7%(黑色箭头)。7 月的两次回调也被忽略,因为它们远低于 7%(红色箭头)。

注意最后一个 ZigZag 线。敏锐的图表分析师会注意到,尽管 QQQQ 仅上涨了 4.13%(43.36 至 45.15),但最后一个 ZigZag 线是向上的。这只是一个临时线,因为 QQQQ 尚未达到 7%的变化阈值。需要到 46.40 才能获得 7%的增长,然后才会有一个永久的 ZigZag 线。如果 QQQQ 在此反弹中未能达到 7%的阈值,然后下跌至 43 以下,这条临时线将消失,之前的 ZigZag 线将从 8 月初的高点继续。

代码
名称:ZigZag
描述:根据给定的DataFrame计算ZigZag指标
import pandas as pd
def ZigZag(df):
df['high_low_range'] = df['high'] - df['low']
df['high_close_range'] = abs(df['high'] - df['close'])
df['low_close_range'] = abs(df['low'] - df['close'])
df['high_low_range_pct'] = df['high_low_range'] / df['close'] * 100
df['high_close_range_pct'] = df['high_close_range'] / df['close'] * 100
df['low_close_range_pct'] = df['low_close_range'] / df['close'] * 100
df['zigzag'] = 0
threshold = 5 # 设置ZigZag功能的灵敏度
for i in range(1, len(df)):
if df.loc[i, 'high_low_range_pct'] >= threshold:
df.loc[i, 'zigzag'] = df.loc[i, 'close']
elif df.loc[i, 'high_close_range_pct'] >= threshold:
df.loc[i, 'zigzag'] = df.loc[i, 'close']
elif df.loc[i, 'low_close_range_pct'] >= threshold:
df.loc[i, 'zigzag'] = df.loc[i, 'close']
else:
df.loc[i, 'zigzag'] = df.loc[i-1, 'zigzag']
return df
# 使用示例
# df = pd.read_csv('your_data.csv')
# df = ZigZag(df)
这个函数计算了ZigZag指标,根据给定的DataFrame中的高、低、收盘价等属性计算出ZigZag值,并根据设定的阈值来确定ZigZag的变化。
积累分布线
计算
计算积累分布线(ADL)有三个步骤。首先,计算资金流乘数。其次,将此值乘以成交量以找到资金流量。第三,创建资金流量的累积总和以形成积累分布线(ADL)。
1\. Money Flow Multiplier = [(Close - Low) - (High - Close)] /(High - Low)
2\. Money Flow Volume = Money Flow Multiplier x Volume for the Period
3\. ADL = Previous ADL + Current Period's Money Flow Volume
资金流乘数在+1 和-1 之间波动。因此,它是资金流量和积累分布线的关键。当收盘价位于高低范围的上半部时,乘数为正,当位于下半部时为负。这是完全合理的。当价格收于周期范围的上半部时,买盘压力大于卖盘压力(反之亦然)。当乘数为正时,积累分布线上升,当乘数为负时,积累分布线下降。

乘数调整了最终进入资金流量的量。除非资金流量乘数处于极端值(+1 或-1),否则实际上会减少交易量。当收盘价处于高位时,乘数为+1,当收盘价处于低位时,乘数为-1。当乘数为+1 时,所有交易量为正,当乘数为-1 时,所有交易量为负。在 0.50 时,只有一半的交易量转化为该时期的资金流量。下表显示了 Research-in-Motion(RIMM)的资金流量乘数、资金流量和累积分布线。请注意,当收盘价强劲时,乘数在 0.50 和 1 之间,当收盘价疲弱时,乘数在-0.50 和-1 之间。

点击这里") 查看 Excel 电子表格中累积分布线的计算。
代码
名称:积累分布线(ADL)
描述:计算资金流乘数、资金流量和积累分布线(ADL)
import pandas as pd
def calculate_ADL(df):
money_flow_multiplier = ((df['close'] - df['low']) - (df['high'] - df['close'])) / (df['high'] - df['low'])
money_flow_volume = money_flow_multiplier * df['volume']
adl = money_flow_volume.cumsum()
return adl
# 使用示例
# adl_values = calculate_ADL(df)
Aroon
计算
Aroon 指标以百分比形式显示,并在 0 到 100 之间波动。Aroon-Up 基于价格高点,而 Aroon-Down 基于价格低点。这两个指标并排绘制,便于比较。SharpCharts 中的默认参数设置为 25,下面的示例基于 25 天。
Aroon-Up = ((25 - Days Since 25-day High)/25) x 100
Aroon-Down = ((25 - Days Since 25-day Low)/25) x 100

随着新高点或新低点之间经过的时间增加,Aroon 会下降。50 是分界点。因为 12.5 天标记着确切的中点,在日线图上不可能出现恰好为 50 的读数。在其他时间框架上是可能的。在日线图上,Aroon 要么低于 50(48),要么高于 50(52)。高于 50 的读数意味着在过去的 12 天或更短时间内记录了新高点或新低点。这是最近一半的回顾期。低于 50 的读数意味着在过去的 13 天或更长时间内记录了新高点或新低点((25-13)/25 x 100 = 48)。这是回顾期的后一半。下表显示了 25 天 Aroon-Up 和 25 天 Aroon-Down 的数值范围。

代码
# 计算 Aroon 指标
def calculate_aroon(df):
df['high_rolling_max'] = df['high'].rolling(window=25).max()
df['low_rolling_min'] = df['low'].rolling(window=25).min()
df['days_since_high'] = 25 - df['high'].shift(1).rolling(window=25).apply(lambda x: x.argmax())
df['days_since_low'] = 25 - df['low'].shift(1).rolling(window=25).apply(lambda x: x.argmin())
df['Aroon-Up'] = ((25 - df['days_since_high']) / 25) * 100
df['Aroon-Down'] = ((25 - df['days_since_low']) / 25) * 100
df.drop(['high_rolling_max', 'low_rolling_min', 'days_since_high', 'days_since_low'], axis=1, inplace=True)
return df
Aroon 振荡器
计算
Aroon-Up 和 Aroon-Down 衡量价格记录 x 天高点或低点以来的周期数。Aroon Up 基于时间和价格高点。Aroon Down 基于时间和价格低点。例如,25 天 Aroon-Up 衡量自 25 天高点以来的天数,而 25 天 Aroon-Down 衡量自 25 天低点以来的天数。这些指标以百分比形式显示,并在 0 和 100 之间波动。Aroon 振荡器简单地是 Aroon-Up 减去 Aroon-Down。SharpCharts 中的默认参数为 25,下面的示例基于 25 天 Aroon 振荡器。
Aroon Up = 100 x (25 - Days Since 25-day High)/25
Aroon Down = 100 x (25 - Days Since 25-day Low)/25
Aroon Oscillator = Aroon-Up - Aroon-Down

简单地计算数字会揭示一些有趣的配对。要达到或超过某个阈值,需要 Aroon-Up 或 Aroon-Down 达到最低水平。例如,当 Aroon-Up 等于 100 且 Aroon-Down 等于 0 时,振荡器等于+100。类似地,当 Aroon-Up 为 0 且 Aroon-Down 为 100 时,Aroon 振荡器等于-100。要使振荡器达到+100,需要一些强劲的上涨价格运动。同样,要使振荡器达到-100,需要一些强劲的下跌价格运动。
等于+40 的 Aroon 振荡器要求 Aroon-Up 至少为 40,这意味着 Aroon-Down 将为 0。正 40 可能来自一系列 Aroon-Up 和 Aroon-Down 的组合(40-0, 44-4, 48-8, 60-20, 72-32, 80-40 或 100-40)。颠倒这些数字以查看可能产生负 40 的组合。
一般来说,相对较高的正数要求 Aroon-Up 相对较高,而相对较低的负数要求 Aroon-Down 相对较高。下表显示了一系列 Aroon-Up 和 Aroon-Down 配对以形成 Aroon 振荡器。

代码
名称:Aroon Oscillator
描述:计算 Aroon 振荡器
---
代码:
def calculate_aroon_oscillator(df):
period = 25
df['Days Since High'] = df['high'].rolling(window=period).apply(lambda x: period - x.idxmax(), raw=True)
df['Days Since Low'] = df['low'].rolling(window=period).apply(lambda x: period - x.idxmin(), raw=True)
df['Aroon Up'] = 100 * (period - df['Days Since High']) / period
df['Aroon Down'] = 100 * (period - df['Days Since Low']) / period
df['Aroon Oscillator'] = df['Aroon Up'] - df['Aroon Down']
df.drop(['Days Since High', 'Days Since Low'], axis=1, inplace=True)
return df
平均趋向指数(ADX)
计算
方向运动是通过比较两个连续低点之间的差异与它们各自高点之间的差异来计算的。
当前高点减去先前高点大于先前低点减去当前低点时,方向运动是正数(加号)。这种所谓的正向方向运动(+DM)等于当前高点减去先前高点,前提是它是正数。负值将简单地输入为零。
当前低点减去先前低点大于当前高点减去先前高点时,方向运动是负数(减号)。这种所谓的负向方向运动(-DM)等于先前低点减去当前低点,前提是它是正数。负值将简单地输入为零。

上图显示了四个方向运动计算示例。第一对显示了强烈的正向方向运动(+DM)的高点之间的巨大正差异。第二对显示了一个外部日,负向方向运动(-DM)占优势。第三对显示了低点之间的巨大差异,形成强烈的负向方向运动(-DM)。最后一对显示了一个内部日,相当于没有方向运动(零)。正向方向运动(+DM)和负向方向运动(-DM)都是负数并恢复为零,因此它们互相抵消。所有内部日都将有零方向运动。
代码
def directional_movement(df):
df['high_shifted'] = df['high'].shift(1)
df['low_shifted'] = df['low'].shift(1)
df['up_move'] = df['high'] - df['high_shifted']
df['down_move'] = df['low_shifted'] - df['low']
df['plus_dm'] = df['up_move'].apply(lambda x: x if x > 0 else 0)
df['minus_dm'] = df['down_move'].apply(lambda x: x if x > 0 else 0)
df.drop(['high_shifted', 'low_shifted', 'up_move', 'down_move'], axis=1, inplace=True)
return df
# 使用示例
df = directional_movement(df)
真实波动幅度(ATR)
计算
通常,平均真实范围(ATR)基于 14 个周期,并可以根据分钟、日、周或月的基础数据进行计算。在这个示例中,ATR 将基于日数据。因为必须有一个起点,第一个 TR 值简单地是最高价减去最低价,而前 14 天的 ATR 是过去 14 天的每日 TR 值的平均值。之后,Wilder 试图通过纳入前一期的 ATR 值来平滑数据。
Current ATR = [(Prior ATR x 13) + Current TR] / 14
- Multiply the previous 14-day ATR by 13.
- Add the most recent day's TR value.
- Divide the total by 14

点击这里查看一个 Excel 电子表格"),展示了 QQQ ATR 计算的开始。
在电子表格示例中,第一个真实范围值(.91)等于最高价减去最低价(黄色单元格)。第一个 14 天 ATR 值(.56)是通过计算前 14 个真实范围值的平均值(蓝色单元格)得出的。随后的 ATR 值使用上述公式进行平滑处理。电子表格中的数值对应下图中的黄色区域。请注意,随着 QQQ 在五月份暴跌并出现许多长蜡烛图,ATR 值激增。

对于那些在家尝试的人,有一些注意事项。首先,就像指数移动平均线(EMAs)一样,ATR 值取决于你从多远的历史数据开始计算。第一个真实范围值简单地是当前最高价减去当前最低价,而第一个 ATR 是前 14 个真实范围值的平均值。真正的 ATR 公式直到第 15 天才开始生效。即便如此,这两个计算的残留效应会略微影响随后的 ATR 值。对于一小部分数据的电子表格数值可能与价格图表上看到的不完全匹配。小数四舍五入也可能会略微影响 ATR 值。在我们的图表中,我们至少计算了 250 个周期(通常更多),以确保我们的 ATR 值更加准确。
代码
名称:ATR
描述:计算平均真实范围(ATR)指标
import pandas as pd
def ATR(df):
df['TR'] = df['high'] - df['low']
df['TR_14'] = df['TR'].rolling(window=14).mean()
df['ATR'] = (df['ATR_14'].shift(1) * 13 + df['TR']) / 14
df.drop(['TR', 'TR_14'], axis=1, inplace=True)
return df
布林带宽度
SharpCharts 计算
( (Upper Band - Lower Band) / Middle Band) * 100
布林带由一个中间带和两个外部带组成。中间带通常设置为 20 个周期的简单移动平均。外部带通常设置为中间带上下 2 个标准差。设置可以根据特定证券或交易风格的特征进行调整。
在计算带宽时,第一步是从上带的值中减去下带的值。这显示了绝对差异。然后将此差异除以中间带,这将使值标准化。然后可以在不同时间段内或与其他证券的带宽值进行比较。

上图显示了纳斯达克 100 ETF(QQQ)的布林带、带宽度和标准差。请注意带宽度如何跟踪标准差(波动性)。两者一起上升和下降。下图显示了一个带有计算示例的电子表格。

代码
# 计算布林带带宽
def calculate_bollinger_band_width(df):
df['middle_band'] = df['close'].rolling(window=20).mean()
df['upper_band'] = df['middle_band'] + 2 * df['close'].rolling(window=20).std()
df['lower_band'] = df['middle_band'] - 2 * df['close'].rolling(window=20).std()
df['band_width'] = ((df['upper_band'] - df['lower_band']) / df['middle_band']) * 100
return df
%B 指标
计算
%B = (Price - Lower Band)/(Upper Band - Lower Band)
%B 的默认设置基于布林带(20,2)的默认设置。这些带子设置在 20 日简单移动平均线的上下 2 个标准差处,这也是中轨。证券价格是收盘价或最后交易价。
代码
# 计算%B指标
def calculate_percent_b(df):
df['middle_band'] = df['close'].rolling(window=20).mean()
df['upper_band'] = df['middle_band'] + 2 * df['close'].rolling(window=20).std()
df['lower_band'] = df['middle_band'] - 2 * df['close'].rolling(window=20).std()
df['percent_b'] = (df['close'] - df['lower_band']) / (df['upper_band'] - df['lower_band'])
return df
查金资金流量
计算
计算查金资金流量(CMF)有四个步骤。下面的示例基于 20 个时期。首先,计算每个时期的资金流量乘数。其次,将此值乘以该时期的交易量,以找到资金流量量。第三,对 20 个时期的资金流量量进行求和,并除以 20 个时期的交易量总和。
1\. Money Flow Multiplier = [(Close - Low) - (High - Close)] /(High - Low)
2\. Money Flow Volume = Money Flow Multiplier x Volume for the Period
3\. 20-period CMF = 20-period Sum of Money Flow Volume / 20 period Sum of Volume
每个时期的资金流量量取决于资金流量乘数。当收盘价位于该时期最高-最低范围的上半部时,该乘数为正;当收盘价位于下半部时,该乘数为负。当收盘价等于最高价时,乘数为 1;当收盘价等于最低价时,乘数为-1。通过这种方式,乘数调整了最终进入资金流量量的量。除非资金流量乘数处于极端值(+1 或-1),否则实际上会减少交易量。

上表显示了使用 Research in Motion(RIMM)的每日数据的一些示例。请注意,当股票在 1 月 5 日收盘时,乘数接近 +1。当股票在 1 月 18 日收盘时,乘数下降到 -0.97。当股票在 12 月 29 日收盘时,乘数接近零(-0.07),股票收于其高低范围的中点附近。点击这里") 查看 Excel 电子表格中 Chaikin Money Flow 的计算示例。
代码
名称:Chaikin Money Flow (CMF)
描述:计算查金资金流量(CMF)
def chaikin_money_flow(df):
money_flow_multiplier = ((df['close'] - df['low']) - (df['high'] - df['close'])) / (df['high'] - df['low'])
money_flow_volume = money_flow_multiplier * df['volume']
df['money_flow_volume'] = money_flow_volume
sum_money_flow_volume = df['money_flow_volume'].rolling(window=20).sum()
sum_volume = df['volume'].rolling(window=20).sum()
df['chaikin_money_flow'] = sum_money_flow_volume / sum_volume
return df
Chaikin Oscillator
计算
计算累积分布线(ADL)是计算 Chaikin Oscillator 的第一步。本文将介绍累积分布线的基本要素。查看我们的 ChartSchool 文章获取详细信息。计算累积分布线(ADL)有三个步骤。首先,计算资金流量乘数。其次,将此值乘以成交量以找到资金流量。第三,创建资金流量的累积总和以形成累积分布线(ADL)。第四,取两个移动平均线之间的差异来计算 Chaikin Oscillator。
1\. Money Flow Multiplier = [(Close - Low) - (High - Close)] /(High - Low)
2\. Money Flow Volume = Money Flow Multiplier x Volume for the Period
3\. ADL = Previous ADL + Current Period's Money Flow Volume
4\. Chaikin Oscillator = (3-day EMA of ADL) - (10-day EMA of ADL)
当资金流量乘数为正时,累积分布线上升;当为负时下降。当收盘价位于周期高低范围的上半部时,该乘数为正;当收盘价位于下半部时,该乘数为负。作为 MACD 类型的振荡器,当较快的 3 日 EMA 移动超过较慢的 10 日 EMA 时,Chaikin Oscillator 变为正。相反,当 3 日 EMA 移动低于 10 日 EMA 时,指标变为负。

上图显示了积累分布线(灰色)与 3 日 EMA(蓝色)和 10 日 EMA(红色)。通用电气(GE)的价格不可见,因此我们可以专注于积累分布线和柴金波动指标之间的关系。请注意,当 3 日 EMA 低于 10 日 EMA 时,柴金波动指标进入负值区域。相反,当 3 日 EMA 穿过 10 日 EMA 时,振荡器变为正值。
代码
名称:累积分布线(ADL)和柴金波动指标描述
描述:根据给定的开盘价、收盘价、最高价、最低价和成交量计算累积分布线(ADL)和柴金波动指标
代码:
import pandas as pd
def calculate_ADL(df):
money_flow_multiplier = ((df['close'] - df['low']) - (df['high'] - df['close'])) / (df['high'] - df['low'])
money_flow_volume = money_flow_multiplier * df['volume']
adl = money_flow_volume.cumsum()
return adl
def calculate_Chaikin_Oscillator(df):
adl = calculate_ADL(df)
ema3 = adl.ewm(span=3, adjust=False).mean()
ema10 = adl.ewm(span=10, adjust=False).mean()
chaikin_oscillator = ema3 - ema10
return chaikin_oscillator
# 使用示例
# df 包含了开盘价、收盘价、最高价、最低价和成交量
# df = pd.DataFrame({'open': [10, 11, 12], 'close': [11, 12, 13], 'high': [13, 14, 15], 'low': [9, 10, 11], 'volume': [1000, 1500, 2000]})
# adl = calculate_ADL(df)
# chaikin_oscillator = calculate_Chaikin_Oscillator(df)
# 查德趋势仪表盘(CTM)
## 计算
查德趋势仪表盘的计算基于以下技术指标:
+ 高、低和收盘价相对于四个不同时间框架(20 天、50 天、75 天和 100 天)的布林带的位置
+ 过去 100 天相对于标准偏差的价格变化
+ 14 天的 RSI 值
+ 任何短期(2 天)价格通道突破的存在
最终得分转换为 0-100 的尺度以便比较。
# 代码
```python
# 计算查德趋势仪表盘得分
def chad_trend(df):
# 计算布林带
df['20_day_ma'] = df['close'].rolling(window=20).mean()
df['20_day_std'] = df['close'].rolling(window=20).std()
df['upper_band_20'] = df['20_day_ma'] + 2 * df['20_day_std']
df['lower_band_20'] = df['20_day_ma'] - 2 * df['20_day_std']
df['50_day_ma'] = df['close'].rolling(window=50).mean()
df['50_day_std'] = df['close'].rolling(window=50).std()
df['upper_band_50'] = df['50_day_ma'] + 2 * df['50_day_std']
df['lower_band_50'] = df['50_day_ma'] - 2 * df['50_day_std']
df['75_day_ma'] = df['close'].rolling(window=75).mean()
df['75_day_std'] = df['close'].rolling(window=75).std()
df['upper_band_75'] = df['75_day_ma'] + 2 * df['75_day_std']
df['lower_band_75'] = df['75_day_ma'] - 2 * df['75_day_std']
df['100_day_ma'] = df['close'].rolling(window=100).mean()
df['100_day_std'] = df['close'].rolling(window=100).std()
df['upper_band_100'] = df['100_day_ma'] + 2 * df['100_day_std']
df['lower_band_100'] = df['100_day_ma'] - 2 * df['100_day_std']
# 计算价格变化相对于标准偏差
df['price_change'] = df['close'].pct_change()
df['std_price_change'] = df['price_change'].rolling(window=100).std()
# 计算 RSI
delta = df['close'].diff()
gain = (delta.where(delta > 0, 0)).rolling(window=14).mean()
loss = (-delta.where(delta < 0, 0)).rolling(window=14).mean()
rs = gain / loss
df['rsi'] = 100 - (100 / (1 + rs))
# 计算价格通道突破
df['high_breakout'] = df['high'] > df['upper_band_20']
df['low_breakout'] = df['low'] < df['lower_band_20']
# 计算得分
df['score'] = ((df['close'] - df['close'].shift(100)) / df['std_price_change'] + df['rsi'] + df['high_breakout'] + df['low_breakout']) / 4 * 100
return df['score']
# 使用示例
chad_trend_score = chad_trend(df)
商品通道指数(CCI)
计算
下面的示例基于 20 周期商品通道指数(CCI)的计算。CCI 周期数也用于简单移动平均和平均偏差的计算。
CCI = (Typical Price - 20-period SMA of TP) / (.015 x Mean Deviation)
Typical Price (TP) = (High + Low + Close)/3
Constant = .015
There are four steps to calculating the Mean Deviation:
First, subtract the most recent 20-period average of the typical price from each period's typical price.
Second, take the absolute values of these numbers.
Third, sum the absolute values.
Fourth, divide by the total number of periods (20).
Lambert 将常数设定为 0.015,以确保大约 70%到 80%的 CCI 值落在-100 和+100 之间。这个百分比还取决于回顾期。较短的 CCI(10 个周期)将更加波动,在+100 和-100 之间的值的百分比较小。相反,较长的 CCI(40 个周期)将在+100 和-100 之间的值有更高的百分比。

点击这里查看在 Excel 电子表格中计算 CCI 的链接")。

代码
名称:CCI指标
描述:根据给定的数据计算商品通道指数(CCI)
import pandas as pd
def calculate_CCI(df):
df['TP'] = (df['High'] + df['Low'] + df['Close']) / 3
df['SMA_TP'] = df['TP'].rolling(window=20).mean()
df['Mean_Deviation'] = df['TP'] - df['SMA_TP']
df['Mean_Deviation'] = df['Mean_Deviation'].abs().rolling(window=20).sum() / 20
df['CCI'] = (df['TP'] - df['SMA_TP']) / (0.015 * df['Mean_Deviation'])
return df['CCI']
# 使用示例
# df['CCI'] = calculate_CCI(df)
# 科波克曲线
## SharpCharts 计算
```py
Coppock Curve = 10-period WMA of 14-period RoC + 11-perod RoC
WMA = Weighted moving average
RoC = Rate-of-Change
变动率指标是一个动量振荡器,它在零线上下振荡。科波克使用了 11 和 14 个周期,因为据一个圣公会牧师说,这是悼念所爱之人丧失的平均哀悼期。科波克推测,股市损失的恢复期将类似于这个时间段。

然后,变动率指标通过加权移动平均进行平滑处理。顾名思义,加权移动平均对最新数据赋予更高的权重,对较旧的数据赋予较低的权重。例如,3 期加权移动平均会将第一个数据点乘以 1,第二个数据点乘以 2,第三个数据点乘以 3。然后,这三个数字的总和除以 6,即权重之和(1 + 2 + 3),以创建加权平均值。下表显示了从 Excel 电子表格中的计算。

点击此处下载此电子表格示例。")
代码
# 名称:Coppock Curve
# 描述:Calculate Coppock Curve using 10-period WMA of 14-period RoC + 11-period RoC
def coppock_curve(df):
df['roc_14'] = (df['close'] / df['close'].shift(14) - 1) * 100
df['roc_11'] = (df['close'] / df['close'].shift(11) - 1) * 100
df['wma_10'] = df['roc_14'].rolling(window=10).apply(lambda x: np.sum(np.arange(1, 11) * x) / 55, raw=True)
df['coppock_curve'] = df['wma_10'] + df['roc_11']
return df
相关系数
计算
相关系数的计算相当复杂,所以可以跳过这一部分。我们只会简单看一些基本内容,以了解其中的方法。这个指标正是经典统计学的核心。第一步是选择两个证券。在这个例子中,我们将使用英特尔(INTC)和纳斯达克 100ETF(QQQ)。换句话说,我们想要看到英特尔和 QQQ 之间的相关程度。下面的 Excel 表格展示了基础工作。

-
INTC 列显示了英特尔在 20 天内的价格,底部显示了平均值。
-
QQQ 列显示了 QQQ 的情况。
-
接下来的两列显示了每个期间的价格平方,底部显示了平均值。
-
最后几列显示了每个期间的 INTC 乘以 QQQ,底部显示了平均值。
利用底部行,我们现在可以计算方差、协方差和相关系数。Excel 公式显示在长公式旁边。结果显示,在 6 月 22 日至 7 月 20 日的 20 天期间,英特尔与纳斯达克 100ETF 表现出强烈的正相关性(+.95)。

这里有一个展示相关系数的 Excel 电子表格")。由于四舍五入问题,一些数字可能略有不同。
代码
## 计算相关系数
import pandas as pd
def calculate_correlation(df):
# 计算 INTC 列和 QQQ 列的均值
intc_mean = df['INTC'].mean()
qqq_mean = df['QQQ'].mean()
# 计算 INTC 列和 QQQ 列的差值
intc_diff = df['INTC'] - intc_mean
qqq_diff = df['QQQ'] - qqq_mean
# 计算 INTC 列和 QQQ 列的平方
intc_sq = intc_diff ** 2
qqq_sq = qqq_diff ** 2
# 计算 INTC 列和 QQQ 列的乘积
intc_qqq = intc_diff * qqq_diff
# 计算相关系数
correlation = intc_qqq.sum() / ((intc_sq.sum() * qqq_sq.sum()) ** 0.5)
return correlation
# 使用示例
# 假设 df 包含了 INTC 和 QQQ 价格数据
correlation = calculate_correlation(df)
print("Correlation between INTC and QQQ:", correlation)
DecisionPoint 价格动量振荡器(PMO)
计算
DecisionPoint 价格动量振荡器是通过采用一个周期变化率并使用两个自定义平滑函数对其进行平滑而导出的。这些自定义平滑函数与指数移动平均线非常相似,但是与真正的 EMA 不同,它们不是将时间周期设置加一来创建平滑乘数(如真正的 EMA 中那样),而是只使用周期本身。
Smoothing Multiplier = (2 / Time period)
Custom Smoothing Function = {Close - Smoothing Function(previous day)} *
Smoothing Multiplier + Smoothing Function(previous day)
PMO Line = 20-period Custom Smoothing of
(10 * 35-period Custom Smoothing of
( ( (Today's Price/Yesterday's Price) * 100) - 100) )
PMO Signal Line = 10-period EMA of the PMO Line

下表显示了亚马逊的 PMO 计算:

要下载包含这些计算的 Excel 电子表格,请点击这里")。
代码
名称:DecisionPoint Price Momentum Oscillator (PMO)
描述:计算价格动量振荡器(PMO)
import pandas as pd
def pmo(df, time_period=20, smoothing_period=35):
# Calculate the Smoothing Multiplier
smoothing_multiplier = 2 / time_period
# Calculate the Custom Smoothing Function
df['Smoothing Function'] = (df['Close'] - df['Smoothing Function'].shift(1)) * smoothing_multiplier + df['Smoothing Function'].shift(1)
# Calculate the 35-period Custom Smoothing
df['35-period Custom Smoothing'] = df['Smoothing Function'].rolling(window=smoothing_period).mean()
# Calculate the Price Momentum Oscillator (PMO) Line
df['PMO Line'] = 20 * df['35-period Custom Smoothing'].rolling(window=10).mean()
# Calculate the PMO Signal Line
df['PMO Signal Line'] = df['PMO Line'].ewm(span=10, adjust=False).mean()
return df
# Assuming df is the DataFrame containing the necessary columns (open, close, high, low, volume)
df = pmo(df)
去趋势价格振荡器(DPO)
计算
Price {X/2 + 1} periods ago less the X-period simple moving average.
X refers to the number of periods used to calculate the Detrended Price
Oscillator. A 20-day DPO would use a 20-day SMA that is displaced by 11
periods {20/2 + 1 = 11}. This displacement shifts the 20-day SMA 11 days to the left, which actually puts it in the middle of the look-back
period. The value of the 20-day SMA is then subtracted from the price
in the middle of this look-back period. In short, DPO(20) equals price
11 days ago less the 20-day SMA.
代码
# Calculate Detrended Price Oscillator
def detrended_price_oscillator(df, X):
sma = df['close'].rolling(window=X).mean()
dpo = df['close'].shift(-int(X/2 + 1)) - sma
return dpo
价格运动便利性
SharpCharts 计算
EMV 公式有三部分:移动距离、成交量和高低范围。首先,移动距离是通过比较当前周期的中点与前一周期的中点(即高加低除以二)来计算的。当当前中点高于前一中点时,移动距离为正,当当前中点低于前一中点时,移动距离为负。移动距离在下面的公式中显示为分子。
Distance Moved = ((H + L)/2 - (Prior H + Prior L)/2)
Box Ratio = ((V/100,000,000)/(H - L))
1-Period EMV = ((H + L)/2 - (Prior H + Prior L)/2) / ((V/100,000,000)/(H - L))
14-Period Ease of Movement = 14-Period simple moving average of 1-period EMV
另外两部分构成了盒子比率,它使用了成交量和高低范围。等量图表也是基于成交量和高低范围。盒子比率是 EMV 的分母。请注意,成交量除以 100,000,000 以保持与其他数字的相关性。
相对较低的成交量和相对较大的高低范围将产生较小的分母(盒子比率),这意味着由于除以较小的数字,EMV 值将更大。如果 V/10000000 等于 2,高低范围等于 4,则盒子比率将为 0.50。低成交量的广泛范围意味着价格变动相对容易。换句话说,价格变动不需要太多成交量。
相对较小的高低范围和高成交量将产生较大的分母,这意味着 EMV 值将较小。如果 V/10000000 等于 4,高低范围等于 2,则分母为 2。这意味着价格变动困难,因为在大成交量下高低范围相对较小。
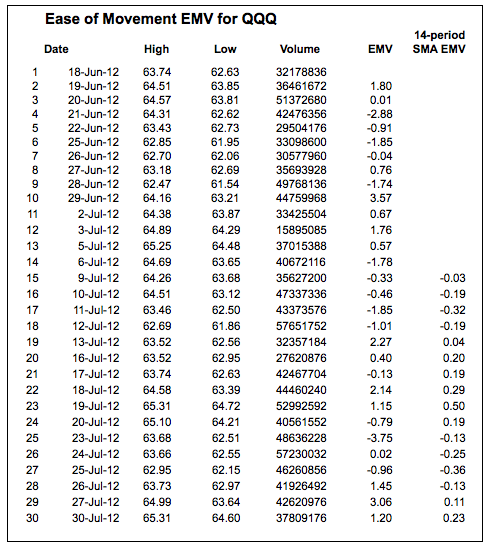
点击这里下载这个电子表格示例。")
代码
# 名称:EMV指标计算
# 描述:根据给定的DataFrame计算EMV指标
def calculate_EMV(df):
df['Distance Moved'] = ((df['high'] + df['low']) / 2 - (df['high'].shift(1) + df['low'].shift(1)) / 2)
df['Box Ratio'] = ((df['volume'] / 100000000) / (df['high'] - df['low']))
df['1-Period EMV'] = df['Distance Moved'] / df['Box Ratio']
df['14-Period Ease of Movement'] = df['1-Period EMV'].rolling(window=14).mean()
return df
力量指数
计算
Force Index(1) = {Close (current period) - Close (prior period)} x Volume
Force Index(13) = 13-period EMA of Force Index(1)
1 期力量指数的计算很简单。只需将前一收盘价减去当前收盘价,然后乘以成交量。超过一天的力量指数只是过去 13 个周期的 1 期力量指数的指数移动平均值。例如,13 期力量指数是过去 13 个周期的 1 期力量指数值的 13 期指数移动平均值。
三个因素影响力量指数的数值。首先,当当前收盘价高于前一收盘价时,力量指数为正值。当当前收盘价低于前一收盘价时,力量指数为负值。其次,移动的幅度决定了成交量的乘数。较大的移动需要较大的乘数,从而相应地影响力量指数。较小的移动产生较小的乘数,降低了影响力。第三,成交量起着关键作用。大幅度的移动伴随大量成交产生高的力量指数数值。小幅度的移动伴随低成交量产生相对较低的力量指数数值。下表显示了辉瑞(PFE)的力量指数计算。第 27 行标记了最大的移动(+84 美分)和最大的成交量(162,619)。这种组合在表中产生了最大的力量指数值(136,600)。
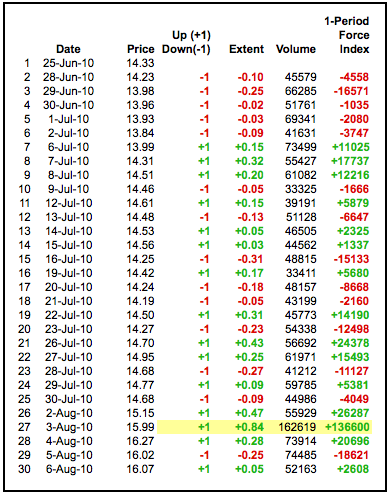
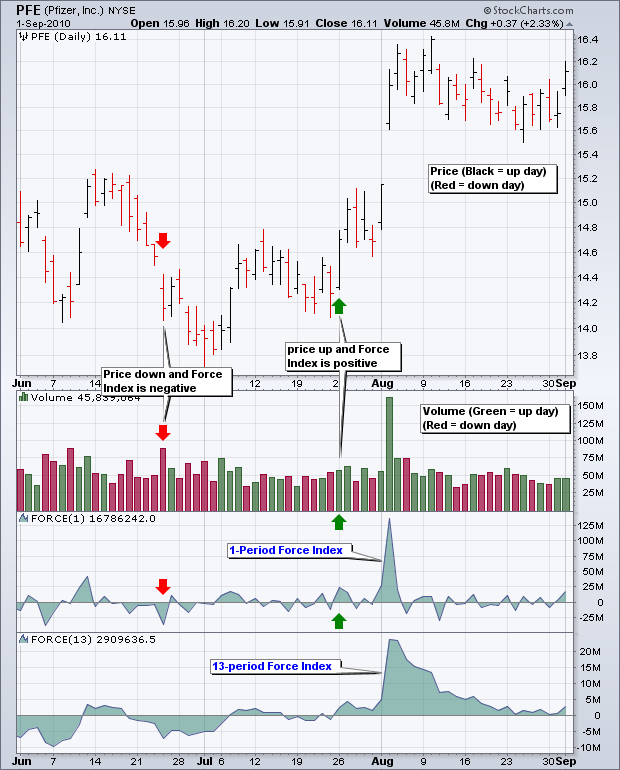
上图展示了力量指数的运作方式。请注意,1 周期力量指数在零线上下波动,看起来相当锯齿状。Elder 建议使用 13 周期 EMA 平滑该指标,以减少正负交叉。图表分析师应该尝试不同的平滑周期,以确定最适合其分析需求的方法。
代码
名称:Force Index
描述:计算1期和13期力量指数
def force_index(df):
df['Force Index(1)'] = (df['Close'] - df['Close'].shift(1)) * df['Volume']
df['Force Index(13)'] = df['Force Index(1)'].ewm(span=13).mean()
return df
质量指数
SharpCharts 计算
质量指数计算涉及四个部分:
Single EMA = 9-period exponential moving average (EMA) of the high-low differential
Double EMA = 9-period EMA of the 9-period EMA of the high-low differential
EMA Ratio = Single EMA divided by Double EMA
Mass Index = 25-period sum of the EMA Ratio
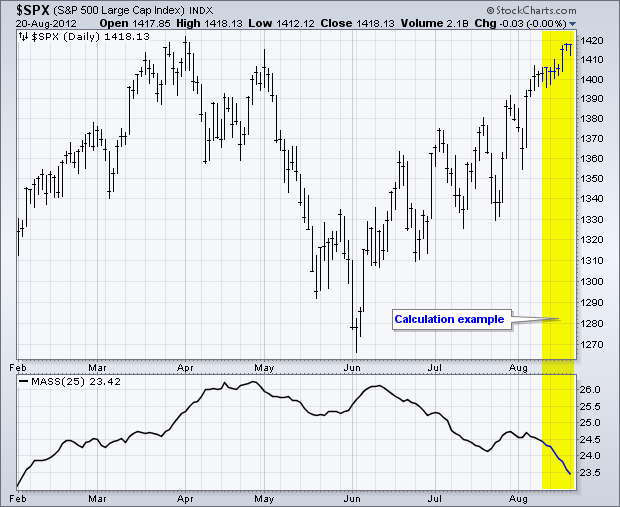
计算相当简单。首先,单一 EMA 提供高低范围的平均值。其次,双重 EMA 对这种波动性指标进行第二次平滑。使用这两个指数移动平均数的比率对数据系列进行归一化。这个比率显示单一 EMA 相对于双重 EMA 变大的时候。最后一步,25 期总和,类似于移动平均线,进一步平滑数据系列。总的来说,随着高低范围的扩大,质量指数上升,随着高低范围的缩小,质量指数下降。下面展示了一个电子表格示例。
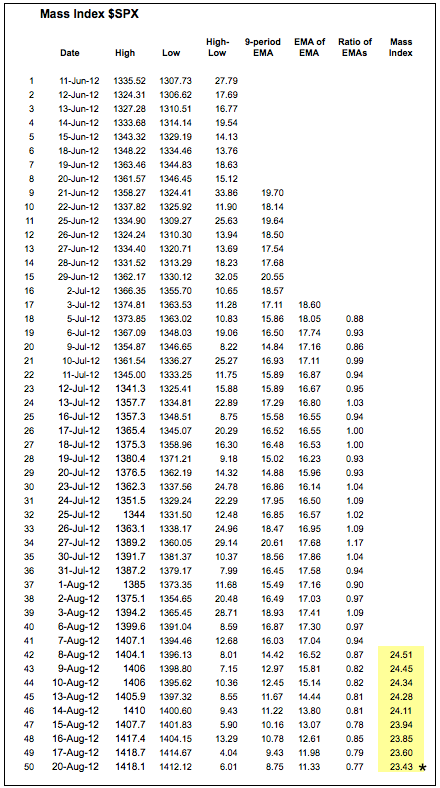
一些电子表格数值有一分钱的偏差,因为指数移动平均计算的时间跨度不到三个月。SharpCharts 中的计算时间跨度为两年,这使指数移动平均计算更加稳健。点击这里下载这个电子表格示例。")
代码
名称:质量指数(Mass Index)
描述:根据给定的开盘价、收盘价、最高价和最低价计算质量指数
import pandas as pd
def mass_index(df):
df['high_low_diff'] = df['high'] - df['low']
df['single_ema'] = df['high_low_diff'].ewm(span=9, min_periods=0, adjust=False).mean()
df['double_ema'] = df['single_ema'].ewm(span=9, min_periods=0, adjust=False).mean()
df['ema_ratio'] = df['single_ema'] / df['double_ema']
df['mass_index'] = df['ema_ratio'].rolling(window=25).sum()
return df
# 使用示例
df = pd.DataFrame({
'open': [100, 110, 105, 120, 115],
'close': [105, 115, 118, 125, 120],
'high': [110, 120, 122, 130, 128],
'low': [95, 105, 108, 118, 112],
'volume': [1000, 1200, 1500, 800, 1000]
})
result = mass_index(df)
print(result)
MACD(移动平均线收敛/发散振荡器)
计算
MACD Line: (12-day EMA - 26-day EMA)
Signal Line: 9-day EMA of MACD Line
MACD Histogram: MACD Line - Signal Line
MACD 线是 12 天的指数移动平均线(EMA)减去 26 天的 EMA。这些移动平均线使用收盘价。MACD 线的 9 天 EMA 与指标一起绘制,作为信号线并识别转折点。MACD 柱状图表示 MACD 与其 9 天 EMA(信号线)之间的差异。当 MACD 线高于其信号线时,柱状图为正,当 MACD 线低于其信号线时,柱状图为负。
12、26 和 9这些数值是 MACD 中典型的设置,然而根据您的交易风格和目标,可以替换其他数值。
代码
# 计算MACD指标
def calculate_macd(df):
# 计算12天EMA
ema_12 = df['close'].ewm(span=12, adjust=False).mean()
# 计算26天EMA
ema_26 = df['close'].ewm(span=26, adjust=False).mean()
# 计算MACD线
macd_line = ema_12 - ema_26
# 计算信号线
signal_line = macd_line.ewm(span=9, adjust=False).mean()
# 计算MACD柱状图
macd_histogram = macd_line - signal_line
return macd_line, signal_line, macd_histogram
# 将计算结果添加到DataFrame中
df['MACD Line'], df['Signal Line'], df['MACD Histogram'] = calculate_macd(df)
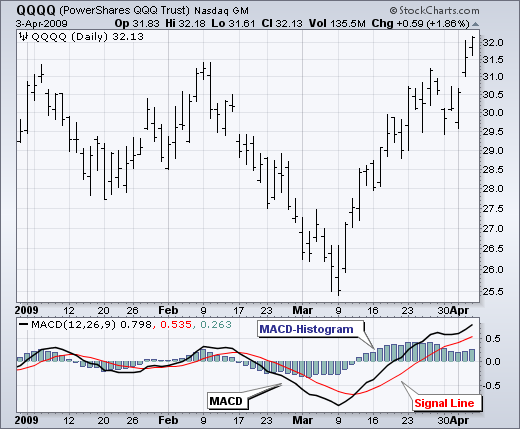
MACD-Histogram
计算
MACD: (12-day EMA - 26-day EMA)
Signal Line: 9-day EMA of MACD
MACD Histogram: MACD - Signal Line
标准 MACD 是 12 日指数移动平均线(EMA)减去 26 日 EMA。收盘价用于形成移动平均线,因此 MACD。MACD 的 9 日 EMA 被绘制在旁边,作为一个信号线,用于识别指标的转折点。MACD-Histogram 代表 MACD 和其 9 日 EMA 信号线之间的差异。当 MACD 高于其 9 日 EMA 时,直方图为正,当 MACD 低于其 9 日 EMA 时,直方图为负。
代码
# 计算 MACD 指标
def calculate_MACD(df):
df['12-day EMA'] = df['close'].ewm(span=12, adjust=False).mean()
df['26-day EMA'] = df['close'].ewm(span=26, adjust=False).mean()
df['MACD'] = df['12-day EMA'] - df['26-day EMA']
df['Signal Line'] = df['MACD'].ewm(span=9, adjust=False).mean()
df['MACD Histogram'] = df['MACD'] - df['Signal Line']
return df
# 使用示例
df = calculate_MACD(df)
print(df[['MACD', 'Signal Line', 'MACD Histogram']])
资金流指数(MFI)
计算
资金流指数计算涉及几个步骤。下面的示例基于 14 周期的资金流指数,这是 SharpCharts 的默认设置和创建者推荐的设置。
Typical Price = (High + Low + Close)/3
Raw Money Flow = Typical Price x Volume
Money Flow Ratio = (14-period Positive Money Flow)/(14-period Negative Money Flow)
Money Flow Index = 100 - 100/(1 + Money Flow Ratio)
首先,注意原始资金流是基本上是美元交易量,因为公式是交易量乘以典型价格。当典型价格从一个周期到下一个周期上涨时,原始资金流是正的,当典型价格下跌时是负的。当典型价格不变时,不使用原始资金流值。第 3 步中的资金流比率形成了资金流指数(MFI)的基础。正负资金流在回顾期(14)内求和,正资金流总和除以负资金流总和得到比率。然后应用 RSI 公式创建一个成交量加权指标。下表显示了从 Excel 电子表格中提取的计算示例。
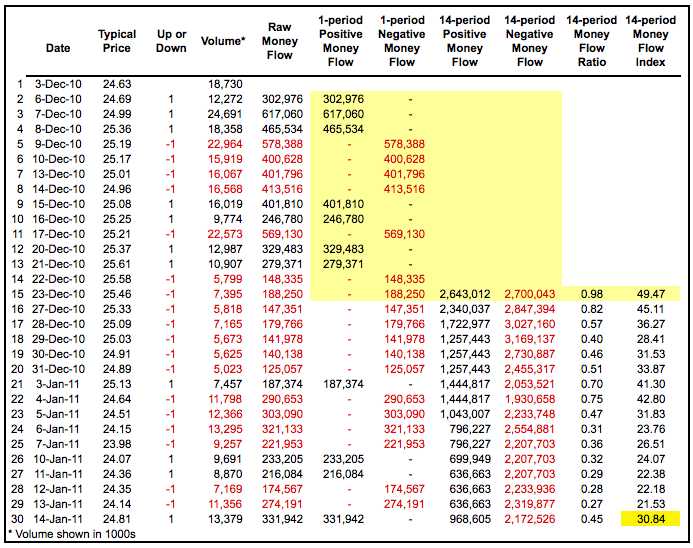
点击这里")查看 Excel 电子表格中的 MFI 计算。
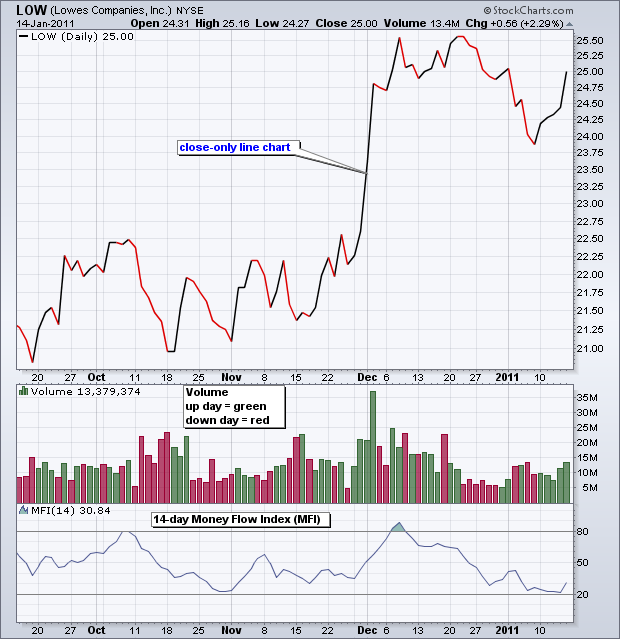
代码
名称:资金流指数
描述:计算资金流指数(MFI)
import pandas as pd
def money_flow_index(df, period=14):
df['typical_price'] = (df['high'] + df['low'] + df['close']) / 3
df['raw_money_flow'] = df['typical_price'] * df['volume']
df['positive_money_flow'] = df['raw_money_flow'].where(df['typical_price'] > df['typical_price'].shift(1), 0)
df['negative_money_flow'] = df['raw_money_flow'].where(df['typical_price'] < df['typical_price'].shift(1), 0)
df['money_flow_ratio'] = df['positive_money_flow'].rolling(window=period).sum() / df['negative_money_flow'].rolling(window=period).sum()
df['money_flow_index'] = 100 - 100 / (1 + df['money_flow_ratio'])
df.drop(['typical_price', 'raw_money_flow', 'positive_money_flow', 'negative_money_flow', 'money_flow_ratio'], axis=1, inplace=True)
return df
# 使用示例
df = pd.DataFrame({
'open': [100, 110, 105, 120, 125],
'high': [120, 130, 115, 130, 130],
'low': [90, 100, 95, 110, 120],
'close': [110, 120, 110, 125, 125],
'volume': [1000, 1500, 1200, 2000, 1800]
})
df = money_flow_index(df)
print(df)
负量指数 (NVI)
SharpCharts 计算
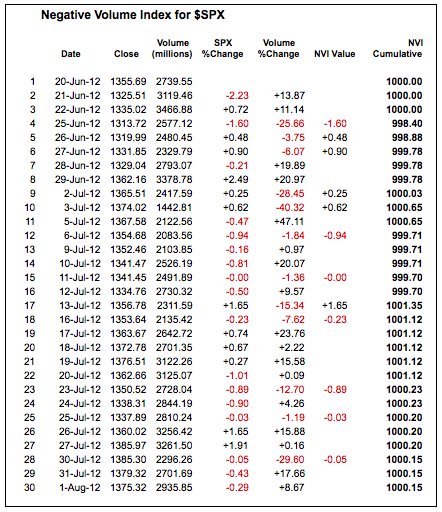
负量指数有两个版本。在原始版本中,戴萨特通过在一个周期到另一个周期成交量减少时添加净进步来形成一个累积线。净进步等于上涨股票数减去下跌股票数。当成交量从一个周期增加到另一个周期时,累积 NVI 线保持不变。换句话说,什么也没做。股市逻辑的诺曼·福斯巴克通过用百分比价格变化替代净进步来调整了该指标。SharpCharts 公式使用了这个福斯巴克版本。
1\. Cumulative NVI starts at 1000
2\. Add the Percentage Price Change to Cumulative NVI when Volume Decreases
3\. Cumulative NVI is Unchanged when Volume Increases
4\. Apply a 255-day EMA for Signals
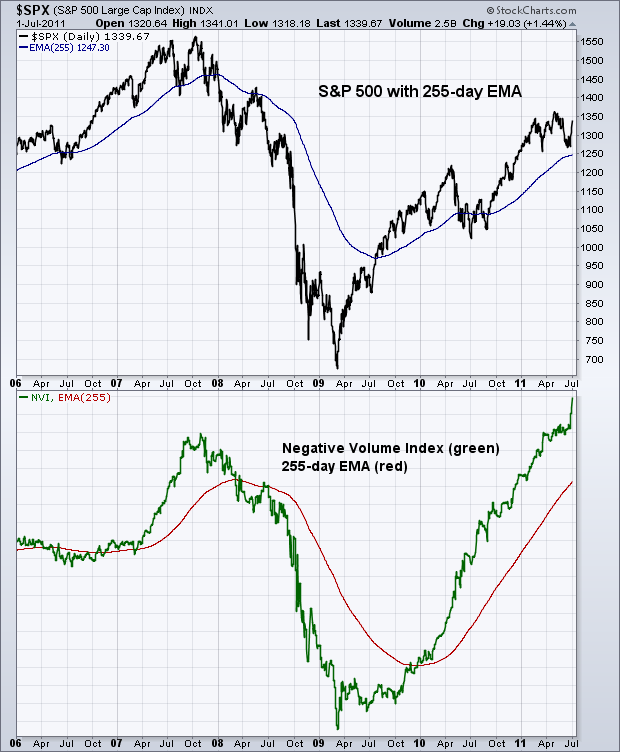
电子表格示例详细展示了计算过程。价格 % 变化乘以 100,以减少所需的小数位数。首先注意成交量 % 变化列。当这个值为负时,标普 500 的百分比变化被输入到 NVI 值列中。当这个值为正时,NVI 值列中不会出现任何内容。从 1000 开始,每个周期应用 NVI 值,以创建一个仅在成交量减少时变化的累积指标。
点击此处下载此电子表格示例。")
代码
名称:Negative Volume Index (NVI)
描述:Calculate the Negative Volume Index (NVI) based on the SharpCharts formula
import pandas as pd
def calculate_NVI(df):
df['price_change'] = df['close'].pct_change() * 100
df['NVI'] = 1000
for i in range(1, len(df)):
if df['volume'][i] < df['volume'][i-1]:
df['NVI'][i] = df['NVI'][i-1] + df['price_change'][i]
else:
df['NVI'][i] = df['NVI'][i-1]
df['NVI_EMA'] = df['NVI'].ewm(span=255, min_periods=255).mean()
return df[['NVI', 'NVI_EMA']]
# Example usage
nvi_data = calculate_NVI(df)
print(nvi_data)
成交量平衡(OBV)
计算
成交量平衡(OBV)线简单地是正向和负向成交量的累计总和。当收盘价高于前一个收盘价时,该时期的成交量为正。当收盘价低于前一个收盘价时,该时期的成交量为负。
If the closing price is above the prior close price then:
Current OBV = Previous OBV + Current Volume
If the closing price is below the prior close price then:
Current OBV = Previous OBV - Current Volume
If the closing prices equals the prior close price then:
Current OBV = Previous OBV (no change)
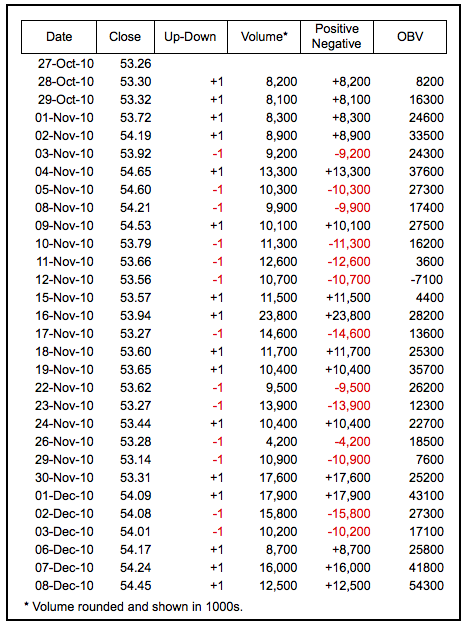
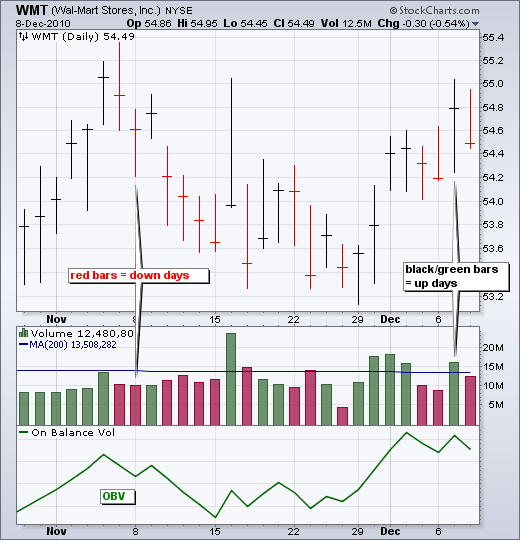
上表中的数据来自沃尔玛(WMT)。成交量数据已四舍五入,并以千为单位显示。换句话说,8200 实际上等于 820 万股。首先,我们必须确定沃尔玛是收盘上涨(+1)还是下跌(-1)。这个数字现在被用作成交量乘数,用于计算正向或负向成交量。最后一列(OBV)形成正向/负向成交量的累计总和。因为 OBV 必须从某个地方开始,第一个值(8200)只是等于第一个时期的正向/负向成交量。下面的图表显示了沃尔玛的成交量和 OBV。
代码
# 计算成交量平衡(OBV)线
def calculate_obv(df):
obv = [0] # 初始化 OBV 列表,第一个值为 0
for i in range(1, len(df)):
if df['close'][i] > df['close'][i-1]:
obv.append(obv[-1] + df['volume'][i]) # 当收盘价高于前一个收盘价时,正向成交量累加
elif df['close'][i] < df['close'][i-1]:
obv.append(obv[-1] - df['volume'][i]) # 当收盘价低于前一个收盘价时,负向成交量累加
else:
obv.append(obv[-1]) # 当收盘价等于前一个收盘价时,OBV 保持不变
df['obv'] = obv # 将计算得到的 OBV 列表添加到 DataFrame 中
return df
# 使用示例
df = calculate_obv(df)
print(df)
百分比价格振荡器
计算
Percentage Price Oscillator (PPO): {(12-day EMA - 26-day EMA)/26-day EMA} x 100
Signal Line: 9-day EMA of PPO
PPO Histogram: PPO - Signal Line
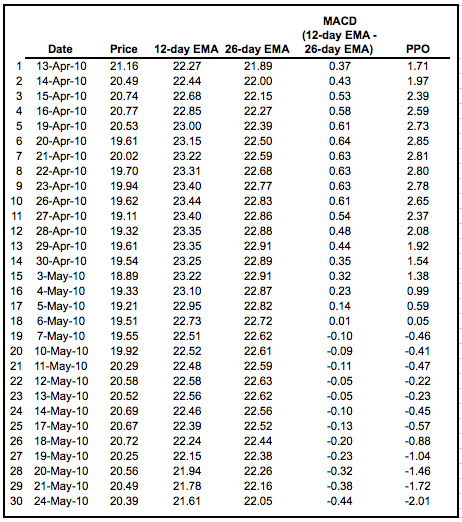
虽然 MACD 衡量两个移动平均线之间的绝对差值,但 PPO 通过将差值除以较慢的移动平均线(26 天 EMA)使其成为相对值。PPO 简单地是 MACD 值除以较长的移动平均线。结果乘以 100,将小数点移动两位。下表显示了英特尔(INTC)的 12 天 EMA、26 天 EMA、MACD 和 PPO 的值。英特尔的价格在低 20 美元左右,MACD 值范围从 -44 美分到 +64 美分。PPO 将这些值转换为百分比,范围从 -2.01 到 +2.85。使用百分比更容易随时间比较水平。-2.01 相当于 -2.01%,而 +2.85 相当于 +2.85%。
点击此处下载此电子表格示例。")
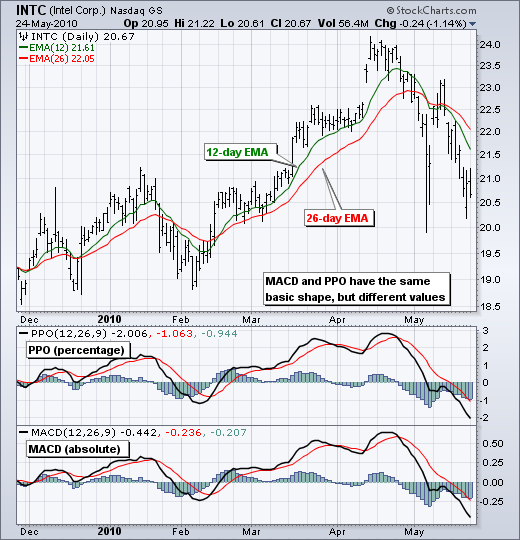
标准 PPO 基于 12 日指数移动平均线(EMA)和 26 日 EMA,但这些参数可以根据投资者或交易者的偏好进行更改。收盘价格用于计算移动平均线,因此 PPO 信号应根据收盘价格进行衡量。PPO 的 9 日 EMA 被绘制为信号线,以识别指标的上升和下降。
代码
# 计算PPO指标
def calculate_PPO(df):
df['12-day EMA'] = df['close'].ewm(span=12, adjust=False).mean()
df['26-day EMA'] = df['close'].ewm(span=26, adjust=False).mean()
df['PPO'] = ((df['12-day EMA'] - df['26-day EMA']) / df['26-day EMA']) * 100
df['Signal Line'] = df['PPO'].ewm(span=9, adjust=False).mean()
df['PPO Histogram'] = df['PPO'] - df['Signal Line']
return df
百分比成交量振荡器
计算
Percentage Volume Oscillator (PVO):
((12-day EMA of Volume - 26-day EMA of Volume)/26-day EMA of Volume) x 100
Signal Line: 9-day EMA of PVO
PVO Histogram: PVO - Signal Line
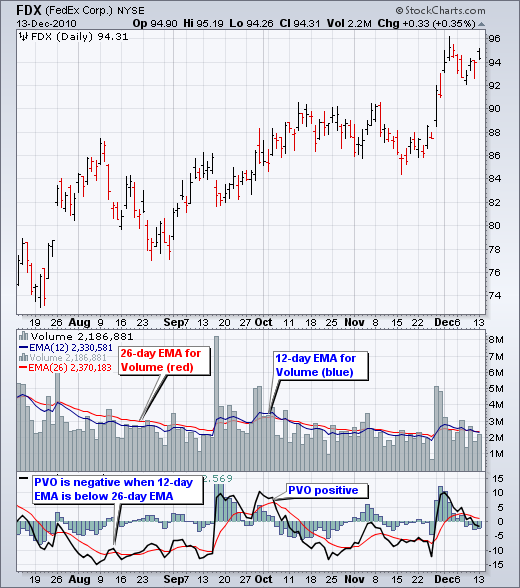
PVO 的默认设置为 (12,26,9),与 MACD 或 PPO 相同。这意味着当 12 天成交量 EMA 上穿 26 天成交量 EMA 时,PVO 为正。当 12 天成交量 EMA 下穿 26 天成交量 EMA 时,PVO 为负。
正负程度取决于远近。PVO 等于 5 表示 12 天成交量 EMA 比 26 天成交量 EMA 高 5%。PVO 等于 -3% 表示 12 天成交量 EMA 比 26 天成交量 EMA 低 3%。
PVO-Histogram 的作用类似于 MACD 和 PPO 直方图。当 PVO 在其信号线(9 天 EMA)上方交易时,PVO-Histogram 为正。当 PVO 低于其信号线时,PVO-Histogram 为负。请注意,PVO 乘以 100,以将小数点移动两位。
代码
def calculate_pvo(df):
df['12-day EMA of Volume'] = df['volume'].ewm(span=12, adjust=False).mean()
df['26-day EMA of Volume'] = df['volume'].ewm(span=26, adjust=False).mean()
df['PVO'] = ((df['12-day EMA of Volume'] - df['26-day EMA of Volume']) / df['26-day EMA of Volume']) * 100
df['Signal Line'] = df['PVO'].ewm(span=9, adjust=False).mean()
df['PVO Histogram'] = df['PVO'] - df['Signal Line']
return df
价格相对 / 相对强度
计算
Price Relative = Base Security / Comparative Security
Ratio Symbol Close = Close of First Symbol / Close of Second Symbol
Ratio Symbol Open = Open of First Symbol / Close of Second Symbol
Ratio Symbol High = High of First Symbol / Close of Second Symbol
Ratio Symbol Low = Low of First Symbol / Close of Second Symbol
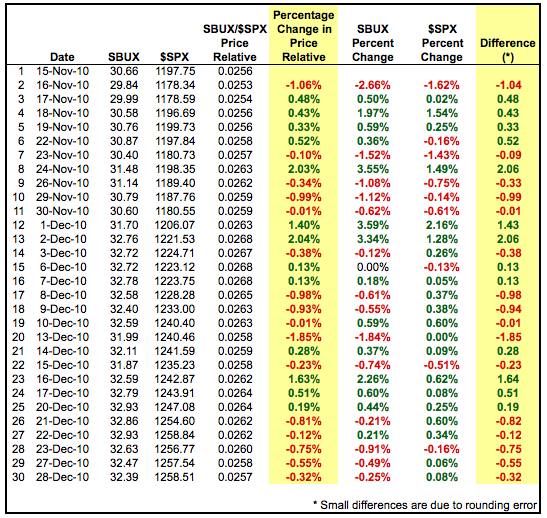
价格相对指标简单地是基础证券除以比较证券。通常,基础证券是一支股票,基准是标普 500 指数。例如,图表分析师可以使用价格相对指标显示星巴克(SBUX)相对于标普 500 指数(\(SPX)的表现。这只是星巴克的价格除以标普 500 指数。星巴克属于消费者自由选择行业。图表分析师还可以查看星巴克相对于消费者自由选择 SPDR(XLY)的表现,使用适当的[比率符号](http://stockcharts.com/docs/doku.php?id=data#ratio_symbols_relative_strength "http://stockcharts.com/docs/doku.php?id=data#ratio_symbols_relative_strength")(SBUX:XLY)。图表分析师还可以查看板块表现相对于标普 500 指数(XLY:\)SPX)。
点击这里下载此电子表格示例。")
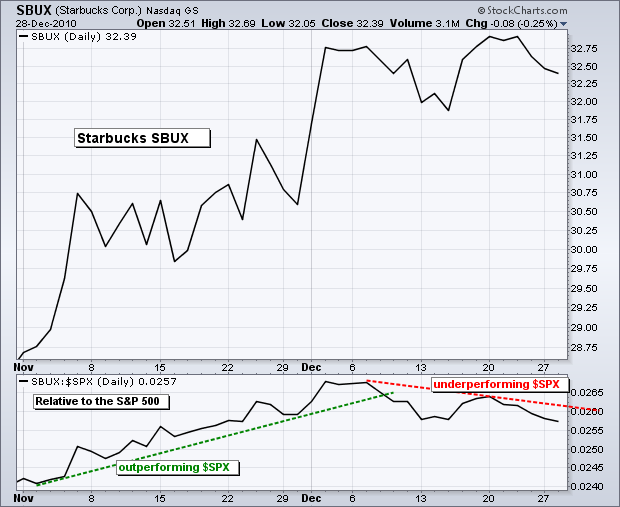
上表显示了星巴克/标普 500 价格相对性。第二行中的第一个值为 0.0256(30.66/1197.75)。当星巴克的涨幅超过标普 500 或跌幅低于标普 500 时,这个比率会增加。当星巴克的涨幅低于标普 500 或跌幅超过标普 500 时,这个比率会减少。为了参考,表中还显示了星巴克和标普 500 的百分比变化。星巴克的百分比变化减去标普 500 的百分比变化也等于价格相对性的日变化。在第二行中,注意到星巴克下跌了 2.66%,而标普 500 下跌了 1.62%。价格相对性下降(-1.04%),因为星巴克的跌幅超过了标普 500。第三行显示价格相对性上升,因为星巴克(+0.50%)的涨幅高于标普 500(+0.02%)。下图展示了价格相对性的实际情况。
代码
名称:价格相对指标
描述:计算基础证券与比较证券的价格相对指标
def price_relative(df, base_security, comparative_security):
df['Price Relative'] = df[base_security] / df[comparative_security]
return df
名称:比率符号收盘价
描述:计算第一个符号与第二个符号的收盘价比率
def ratio_symbol_close(df, first_symbol, second_symbol):
df['Ratio Symbol Close'] = df[first_symbol] / df[second_symbol]
return df
名称:比率符号开盘价
描述:计算第一个符号与第二个符号的开盘价比率
def ratio_symbol_open(df, first_symbol, second_symbol):
df['Ratio Symbol Open'] = df[first_symbol] / df[second_symbol]
return df
名称:比率符号最高价
描述:计算第一个符号与第二个符号的最高价比率
def ratio_symbol_high(df, first_symbol, second_symbol):
df['Ratio Symbol High'] = df[first_symbol] / df[second_symbol]
return df
名称:比率符号最低价
描述:计算第一个符号与第二个符号的最低价比率
def ratio_symbol_low(df, first_symbol, second_symbol):
df['Ratio Symbol Low'] = df[first_symbol] / df[second_symbol]
return df
知识确定事物(KST)
SharpCharts 计算
即使 KST 的公式看起来很复杂,但它实际上是一个相当直观的指标。它只是四个不同变化率的加权平均值,经过平滑处理。例如,计算 10 周期的变化率,然后用 10 周期的简单移动平均进行平滑处理。下图显示了四个不同的变化率指标及其适当的移动平均线进行平滑处理。
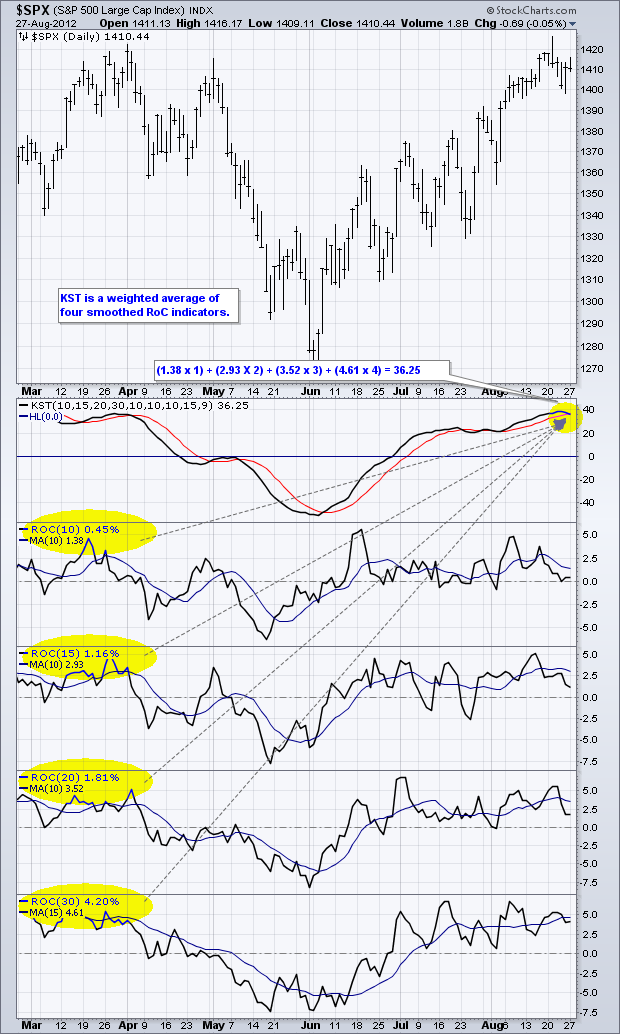
下方的公式框显示了四种不同组合及其默认设置。这些组合然后被加权和求和。最短的时间框架承载最小的权重(1),而最长的时间框架承载最大的权重(4)。添加了一个 9 周期的简单移动平均线作为信号线。
RCMA1 = 10-Period SMA of 10-Period Rate-of-Change
RCMA2 = 10-Period SMA of 15-Period Rate-of-Change
RCMA3 = 10-Period SMA of 20-Period Rate-of-Change
RCMA4 = 15-Period SMA of 30-Period Rate-of-Change
KST = (RCMA1 x 1) + (RCMA2 x 2) + (RCMA3 x 3) + (RCMA4 x 4)
Signal Line = 9-period SMA of KST
默认参数如下:KST(10,15,20,30,10,10,10,15,9)。前四个数字代表变化率设置,后四个代表这些变化率指标的移动平均线,最后一个数字是信号线移动平均线。
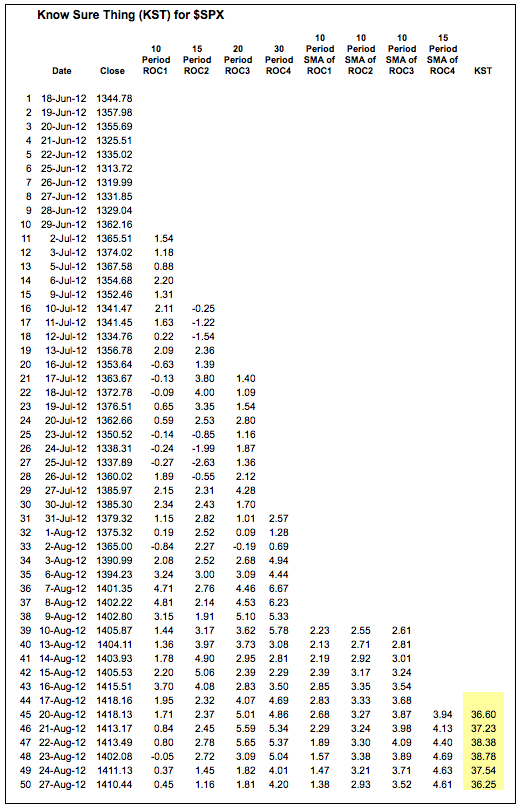
点击这里下载此电子表格示例") 并在家里尝试。
代码
名称:KST
描述:根据给定的开盘价、收盘价、最高价、最低价和成交量计算知识强弱指标(KST)
代码:
def calculate_KST(df):
df['ROC_10'] = df['close'].pct_change(10)
df['ROC_15'] = df['close'].pct_change(15)
df['ROC_20'] = df['close'].pct_change(20)
df['ROC_30'] = df['close'].pct_change(30)
df['RCMA1'] = df['ROC_10'].rolling(10).mean()
df['RCMA2'] = df['ROC_15'].rolling(10).mean()
df['RCMA3'] = df['ROC_20'].rolling(10).mean()
df['RCMA4'] = df['ROC_30'].rolling(15).mean()
df['KST'] = (df['RCMA1'] * 1) + (df['RCMA2'] * 2) + (df['RCMA3'] * 3) + (df['RCMA4'] * 4)
df['Signal Line'] = df['KST'].rolling(9).mean()
return df
马丁·普林的特别 K
计算
特别 K 是几种不同变化率加权平均数的总和。这些周期和权重是基于多年的市场观察而选择的。
Special K = 10 Period Simple Moving Average of ROC(10) * 1
+ 10 Period Simple Moving Average of ROC(15) * 2
+ 10 Period Simple Moving Average of ROC(20) * 3
+ 15 Period Simple Moving Average of ROC(30) * 4
+ 50 Period Simple Moving Average of ROC(40) * 1
+ 65 Period Simple Moving Average of ROC(65) * 2
+ 75 Period Simple Moving Average of ROC(75) * 3
+100 Period Simple Moving Average of ROC(100)* 4
+130 Period Simple Moving Average of ROC(195)* 1
+130 Period Simple Moving Average of ROC(265)* 2
+130 Period Simple Moving Average of ROC(390)* 3
+195 Period Simple Moving Average of ROC(530)* 4
请注意,至少需要 725 个数据点才能准确计算此指标。如果数据较少,则计算的最后一行将被跳过。
代码
# 计算 Special K 指标
def calculate_special_k(df):
if len(df) < 725:
print("数据点不足,无法计算 Special K 指标")
return
df['ROC_10'] = (df['close'] - df['close'].shift(10)) / df['close'].shift(10) * 100
df['ROC_15'] = (df['close'] - df['close'].shift(15)) / df['close'].shift(15) * 100
df['ROC_20'] = (df['close'] - df['close'].shift(20)) / df['close'].shift(20) * 100
df['ROC_30'] = (df['close'] - df['close'].shift(30)) / df['close'].shift(30) * 100
df['ROC_40'] = (df['close'] - df['close'].shift(40)) / df['close'].shift(40) * 100
df['ROC_65'] = (df['close'] - df['close'].shift(65)) / df['close'].shift(65) * 100
df['ROC_75'] = (df['close'] - df['close'].shift(75)) / df['close'].shift(75) * 100
df['ROC_100'] = (df['close'] - df['close'].shift(100)) / df['close'].shift(100) * 100
df['ROC_195'] = (df['close'] - df['close'].shift(195)) / df['close'].shift(195) * 100
df['ROC_265'] = (df['close'] - df['close'].shift(265)) / df['close'].shift(265) * 100
df['ROC_390'] = (df['close'] - df['close'].shift(390)) / df['close'].shift(390) * 100
df['ROC_530'] = (df['close'] - df['close'].shift(530)) / df['close'].shift(530) * 100
df['Special_K'] = (df['ROC_10'].rolling(10).mean() * 1 +
df['ROC_15'].rolling(10).mean() * 2 +
df['ROC_20'].rolling(10).mean() * 3 +
df['ROC_30'].rolling(15).mean() * 4 +
df['ROC_40'].rolling(50).mean() * 1 +
df['ROC_65'].rolling(65).mean() * 2 +
df['ROC_75'].rolling(75).mean() * 3 +
df['ROC_100'].rolling(100).mean() * 4 +
df['ROC_195'].rolling(130).mean() * 1 +
df['ROC_265'].rolling(130).mean() * 2 +
df['ROC_390'].rolling(130).mean() * 3 +
df['ROC_530'].rolling(195).mean() * 4)
return df
变动率(ROC)
计算
ROC = [(Close - Close n periods ago) / (Close n periods ago)] * 100

点击这里下载此电子表格示例。")
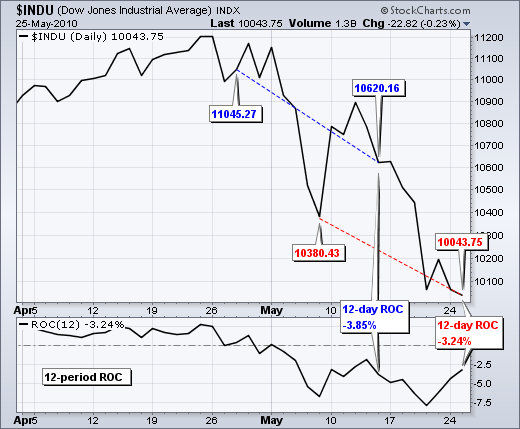
上表显示了 2010 年 5 月道琼斯工业指数的 12 天变动率计算。 黄色单元格显示了从 4 月 28 日到 5 月 14 日的变动率。 实际上是 13 个交易日,但 28 日的收盘价作为 29 日的起点。 蓝色单元格显示了从 5 月 7 日到 5 月 25 日的 12 天变动率。
代码
def calculate_ROC(df, n):
df['ROC'] = ((df['Close'] - df['Close'].shift(n)) / df['Close'].shift(n)) * 100
return df
相对强度指数(RSI)
计算
100
RSI = 100 - --------
1 + RS
RS = Average Gain / Average Loss
为了简化计算说明,RSI 已经被分解为其基本组成部分:RS,平均增益和平均损失。这个 RSI 计算基于 14 个周期,这是 Wilder 在他的书中建议的默认值。损失被表示为正值,而不是负值。
第一次的平均增益和平均损失计算是简单的 14 个周期平均值。
-
第一次平均增益 = 过去 14 个周期的增益总和 / 14。
-
第一次平均损失 = 过去 14 个周期的损失总和 / 14
第二次以及后续的计算基于先前的平均值和当前的盈亏:
-
平均增益 = [(前一次平均增益) x 13 + 当前增益] / 14。
-
平均损失 = [(前一个平均损失) x 13 + 当前损失] / 14。
将先前值加上当前值是一种平滑技术,类似于计算指数移动平均值时使用的技术。这也意味着随着计算周期的延长,RSI 值会变得更准确。SharpCharts 在计算其 RSI 值时,会使用至少 250 个数据点作为起始日期之前的数据点(假设存在这么多数据)。要精确复制我们的 RSI 数值,公式将需要至少 250 个数据点。
Wilder 的公式对 RS 进行归一化,并将其转化为在零和 100 之间波动的振荡器。实际上,RS 的图与 RSI 的图完全相同。归一化步骤使得更容易识别极端值,因为 RSI 是区间限制的。当平均收益等于零时,RSI 为 0。假设为 14 期的 RSI,零的 RSI 值意味着价格在所有 14 期内下跌。没有增益可测量。当平均损失等于零时,RSI 为 100。这意味着价格在所有 14 期内上涨。没有损失可测量。


这里有一个展示 RSI 计算开始过程的 Excel 电子表格")。
注意:平滑过程会影响 RSI 值。RS 值在第一次计算后会被平滑处理。平均损失等于前 14 次损失之和除以 14 进行第一次计算。后续计算会将先前值乘以 13,加上最新值,然后总和除以 14。这样就产生了平滑效果。平均收益也是如此。由于这种平滑处理,RSI 值可能会根据总计算周期而有所不同。250 个周期将比 30 个周期具有更多的平滑效果,这会稍微影响 RSI 值。Stockcharts.com 在可能的情况下回溯 250 天。如果平均损失等于零,则 RS 会出现“除以零”的情况,根据定义 RSI 被设定为 100。同样,当平均收益等于零时,RSI 等于 0。
代码
名称:RSI
描述:计算相对强弱指标(RSI)
def calculate_rsi(df, period=14):
delta = df['close'].diff()
gain = (delta.where(delta > 0, 0)).rolling(window=period).mean()
loss = (-delta.where(delta < 0, 0)).rolling(window=period).mean()
rs = gain / loss
rsi = 100 - (100 / (1 + rs))
return rsi
RRG 相对强度
代码
名称:{title}
描述:计算股票的收益率
---
代码:
def calculate_returns(df):
df['returns'] = df['close'].pct_change()
return df
StockCharts 技术排名(SCTR)
计算
计算 StockCharts 技术排名(SCTR)需要两个步骤。首先,根据六个不同的技术指标对每支股票进行“评分”。这六个指标可以细分为长期、中期和短期三组。下面的框详细介绍了这些指标、相关时间范围和权重。
Long-Term Indicators (weighting)
--------------------------------
* Percent above/below 200-day EMA (30%)
* 125-Day Rate-of-Change (30%)
Medium-Term Indicators (weighting)
----------------------------------
* Percent above/below 50-day EMA (15%)
* 20-day Rate-of-Change (15%)
Short-Term Indicators (weighting)
---------------------------------
* 3-day slope of PPO-Histogram (5%)
* 14-day RSI (5%)
除了 PPO-Histogram 的 3 天斜率外,原始数字用于计算指标得分。例如,如果一支股票比其 200 天移动平均线高出 15%,那么这个指标将为总指标得分贡献 4.5 分(15 x 0.30 = 4.5)。如果 20 天变动率为 -7%,那么这个指标将为总指标得分贡献 -1.05 分(-7 x 0.15 = -1.05)。
对于 PPO-Histogram,如果其斜率大于 +1(即 +45 度),则会为总指标得分贡献 5 分(100 的 5%)。如果 PPO-Histogram 的斜率小于 -45 度,则不会贡献分数。否则,将贡献 ((斜率 + 1) x 50) 的 5%。
在第一轮计算后,StockCharts.com 根据它们的指标得分对这些股票进行排名。请记住,这些股票仅在其组内(如大盘股、中盘股和小盘股)中排名。本文首先将展示一个简化的例子,使用按指标得分排序的十只股票。得分最高的股票获得最高的技术排名(10),而得分最低的股票获得最低的技术排名(1)。然后根据指标得分填充排名。

StockCharts 技术排名提供了更详细的信息。首先,排名范围从 0.00 到 99.99,0 表示绝对最弱,而 99.99 表示绝对最强。没有股票会得到完美的 100 分。其次,StockCharts.com 创建“桶”来对组内的股票进行排序。这些类似于百分位数。以一个包含 500 只股票的范围为例,将创建十个相等的桶,每个桶中有 50 只股票(50 x 10 = 500)。得分最低的 50 只股票进入底部桶,其 SCTR 范围从 0 到 10。得分最高的 50 只股票进入顶部桶,其 SCTR 范围从 90 到 99.99。然后,每个桶将相应填充并在桶内进一步排序。最终结果是 500 只股票从 0 到 99.99 排名,并在排名池中相对均匀地分布。
代码
名称:计算SCTR
描述:根据给定的股票数据计算StockCharts技术排名(SCTR)
import pandas as pd
def calculate_sctr(df):
# 计算长期指标得分
df['long_term_score'] = (df['close'] / df['close'].rolling(window=200).mean() - 1) * 30 + df['close'].pct_change(125) * 30
# 计算中期指标得分
df['medium_term_score'] = (df['close'] / df['close'].rolling(window=50).mean() - 1) * 15 + df['close'].pct_change(20) * 15
# 计算短期指标得分
ppo_slope = df['close'].ewm(span=12).mean() - df['close'].ewm(span=26).mean()
df['short_term_score'] = (ppo_slope.diff(3) / 3) * 5 + df['close'].diff(14).rolling(window=14).apply(lambda x: x[x > 0].mean()) * 5
# 计算总得分
df['sctr'] = df['long_term_score'] + df['medium_term_score'] + df['short_term_score']
return df
# 使用示例
# df = pd.read_csv('stock_data.csv')
# df = calculate_sctr(df)
斜率
计算
斜率基于线性回归(最佳拟合线)。尽管线性回归的公式超出了本文的范围,但可以使用 SharpCharts 中的 Raff 回归通道显示线性回归。该指标在中间显示了一个线性回归,外部趋势线等距分布。斜率等于线性回归的上升/下降比率。上升指的是价格变化。运行指的是时间范围。20 天斜率将是 20 天线性回归的上升/下降比率。如果上升了 4 个点,运行了两天,那么斜率将是 2(4/2 = 2)。如果上升了-6 个点,运行了 2 天,那么斜率将是-3(6/2 = 3)。一般来说,上升期具有正斜率,下降期具有负斜率。斜度取决于上升或下降的陡峭程度。

图表 1 显示了 SPY 与三个不同的 20 天周期(橙色、黄色、蓝色)。每个 20 天周期都显示了一个 20 天的 Raff 回归通道。中间的线性回归代表了这 20 个数据点的“最佳拟合线”。虚线标记了 20 天周期的结束和该价格点的斜率值。第一个周期相对平坦,斜率几乎为正。第二个周期上升,斜率明显为正。第三个周期下降,斜率为负。请记住,随着旧数据点被删除和新数据点被添加,斜率会发生变化。
代码
# 名称:斜率
# 描述:基于线性回归计算斜率
import pandas as pd
import numpy as np
from scipy.stats import linregress
def slope(df):
df['slope'] = np.nan
for i in range(len(df)):
if i >= 20:
x = np.arange(20)
y = df['close'].iloc[i-20:i]
slope, _, _, _, _ = linregress(x, y)
df.at[i, 'slope'] = slope
return df
标准差(波动性)
计算
StockCharts.com 计算的是整体数据集的标准差,这意味着所涉及的周期代表整个数据集,而不是来自更大数据集的样本。计算步骤如下:
-
计算一定周期或观察次数的平均(均值)价格。
-
确定每个周期的偏差(收盘价减去平均价格)。
-
对每个周期的偏差进行平方。
-
求平方偏差的总和。
-
将这个总和除以观察次数。
-
然后标准差等于该数字的平方根。

上面的电子表格显示了使用 QQQQ 数据进行 10 期标准差的示例。请注意,10 期平均值是在第 10 期之后计算的,并且这个平均值适用于所有 10 期。使用这个公式构建一个运行标准差会非常耗时。Excel 有一个更简单的方法,使用 STDEVP 公式。下表显示了使用这个公式的 10 期标准差。这里有一个显示标准差计算的 Excel 电子表格")。


代码
# 计算标准差
def calculate_std(df):
# 计算收盘价的平均值
df['avg_close'] = df['close'].rolling(window=10).mean()
# 计算每个周期的偏差
df['deviation'] = df['close'] - df['avg_close']
# 计算偏差的平方
df['squared_deviation'] = df['deviation'] ** 2
# 求平方偏差的总和
sum_squared_deviation = df['squared_deviation'].sum()
# 将总和除以观察次数
std = (sum_squared_deviation / len(df)) ** 0.5
return std
随机振荡器
计算
%K = (Current Close - Lowest Low)/(Highest High - Lowest Low) * 100
%D = 3-day SMA of %K
Lowest Low = lowest low for the look-back period
Highest High = highest high for the look-back period
%K is multiplied by 100 to move the decimal point two places
默认设置的随机振荡器为 14 个周期,可以是天、周、月或日内时间框架。14 个周期的%K 将使用最近的收盘价,过去 14 个周期内的最高价和最低价。%D 是%K 的 3 天简单移动平均。这条线与%K 一起绘制,作为信号线或触发线。

点击这里下载此电子表格示例。")

代码
名称:随机振荡器(%K 和 %D)
描述:根据给定的收盘价、最高价和最低价计算随机振荡器的 %K 和 %D 值
import pandas as pd
def stochastic_oscillator(df, period=14):
df['Lowest Low'] = df['low'].rolling(window=period).min()
df['Highest High'] = df['high'].rolling(window=period).max()
df['%K'] = (df['close'] - df['Lowest Low']) / (df['Highest High'] - df['Lowest Low']) * 100
df['%D'] = df['%K'].rolling(window=3).mean()
df.drop(['Lowest Low', 'Highest High'], axis=1, inplace=True)
return df[['%K', '%D']]
# 使用示例
# df 包含了 open, close, high, low 四个属性
# df = pd.DataFrame(data)
# result_df = stochastic_oscillator(df)
StochRSI
计算
StochRSI = (RSI - Lowest Low RSI) / (Highest High RSI - Lowest Low RSI)
StochRSI 测量 RSI 相对于其一定周期内的高/低范围的价值。用于计算 StochRSI 的周期数在公式中转移到 RSI。例如,14 天 StochRSI 将使用当前的 14 天 RSI 值和 14 天 RSI 的高低范围。
-
当 RSI 在 14 天内处于最低点时,14 天 StochRSI 等于 0。
-
当 RSI 在 14 天内达到最高点时,14 天 StochRSI 等于 1。
-
当 RSI 处于其 14 天高低范围的中间时,14 天 StochRSI 等于 0.5。
-
当 RSI 接近其 14 天高低范围的低点时,14 天 StochRSI 等于 0.2。
-
当 RSI 接近其 14 天高低范围的高点时,14 天 StochRSI 等于 0.80。

点击这里查看一个 Excel 电子表格"),展示了 StochRSI 计算的开始。
代码
def calculate_StochRSI(df):
n = 14
df['RSI'] = talib.RSI(df['close'], timeperiod=n)
df['Lowest Low RSI'] = df['RSI'].rolling(window=n).min()
df['Highest High RSI'] = df['RSI'].rolling(window=n).max()
df['StochRSI'] = (df['RSI'] - df['Lowest Low RSI']) / (df['Highest High RSI'] - df['Lowest Low RSI'])
return df
TRIX
计算
TRIX 是三重平滑指数移动平均线(EMA)的 1 期百分比变化率,这是一个 EMA 的 EMA 的 EMA。以下是 15 期 TRIX 所涉及的步骤的详细说明。
-
1. 单一平滑的 EMA = 收盘价的 15 日 EMA
-
2. 双重平滑的 EMA = 单一平滑的 EMA 的 15 日 EMA
-
3. 三重平滑的 EMA = 双重平滑的 EMA 的 15 日 EMA
-
4. TRIX = 三重平滑的 EMA 的 1 期百分比变化
下表和图提供了 15 日 EMA、双重平滑的 EMA 和三重平滑的 EMA 的示例。请注意每个 EMA 都会滞后价格一段时间。尽管指数移动平均值更加重视最近的数据,但它们仍包含产生滞后的过去数据。这种滞后随着平滑次数的增加而增加。


蓝线是 SPY 的价格走势图。它显然是四条线中最不平滑(波动最大)的。红线是 15 日 EMA,它最接近价格走势。绿线是双重平滑的 EMA,紫线是三重平滑的 EMA。请注意随着滞后的增加,这两条线变得更加平坦。
只要三重平滑的 15 日 EMA 向下移动,TRIX 就是负的。当三重平滑的 15 日 EMA 向上转变时,TRIX 变为正。额外的平滑确保上涨和下跌被最小化。换句话说,需要超过一天的上涨才能扭转下降趋势。

代码
# 计算TRIX指标
def trix(df):
# 计算单一平滑的EMA
df['single_ema'] = df['close'].ewm(span=15, min_periods=15).mean()
# 计算双重平滑的EMA
df['double_ema'] = df['single_ema'].ewm(span=15, min_periods=15).mean()
# 计算三重平滑的EMA
df['triple_ema'] = df['double_ema'].ewm(span=15, min_periods=15).mean()
# 计算TRIX
df['trix'] = df['triple_ema'].pct_change()
return df
# 使用示例
# df = trix(df)
真实强度指数(TSI)
计算
真实强度指数(TSI)可以分为三部分:双重平滑价格变化、双重平滑绝对价格变化和 TSI 公式。首先,计算一个周期到下一个周期的价格变化。其次,计算这种价格变化的 25 周期 EMA。第三,计算这个 25 周期 EMA 的 13 周期 EMA 以创建双重平滑。绝对价格变化也使用相同的双重平滑技术。在这些初始计算之后,将双重平滑价格变化除以绝对双重平滑价格变化,并乘以 100 以将小数点移动两位。

Double Smoothed PC
------------------
PC = Current Price minus Prior Price
First Smoothing = 25-period EMA of PC
Second Smoothing = 13-period EMA of 25-period EMA of PC
Double Smoothed Absolute PC
---------------------------
Absolute Price Change |PC| = Absolute Value of Current Price minus Prior Price
First Smoothing = 25-period EMA of |PC|
Second Smoothing = 13-period EMA of 25-period EMA of |PC|
TSI = 100 x (Double Smoothed PC / Double Smoothed Absolute PC)
第一部分,即双重平滑价格变化,为 TSI 设定了正面或负面的基调。当双重平滑价格变化为负时,指标为负,当为正时,指标为正。双重平滑绝对价格变化对指标进行了标准化,并限制了随后振荡器的范围。换句话说,该指标衡量了双重平滑价格变化相对于双重平滑绝对价格变化的情况。一连串的大幅正价格变化导致相对较高的正读数,因为这表示强劲的上行动量。一连串的大幅负价格变化将 TSI 推入深度负值区域。

上表来自 Excel 电子表格。请注意,计算中使用了指数移动平均线。这些从简单移动平均线开始,然后使用乘数进行计算,这意味着需要额外的历史数据来达到真实值。点击这里下载此电子表格示例"),并在家里尝试。
代码
名称:真实强度指数(TSI)
描述:根据给定的开盘价、收盘价、最高价和最低价计算真实强度指数(TSI)
代码:
def TSI(df):
df['PC'] = df['close'] - df['close'].shift(1)
df['PC_25_EMA'] = df['PC'].ewm(span=25, min_periods=0, adjust=False).mean()
df['PC_25_EMA_13_EMA'] = df['PC_25_EMA'].ewm(span=13, min_periods=0, adjust=False).mean()
df['|PC|'] = abs(df['close'] - df['close'].shift(1))
df['|PC|_25_EMA'] = df['|PC|'].ewm(span=25, min_periods=0, adjust=False).mean()
df['|PC|_25_EMA_13_EMA'] = df['|PC|_25_EMA'].ewm(span=13, min_periods=0, adjust=False).mean()
df['TSI'] = 100 * (df['PC_25_EMA_13_EMA'] / df['|PC|_25_EMA_13_EMA'])
df.drop(['PC', 'PC_25_EMA', 'PC_25_EMA_13_EMA', '|PC|', '|PC|_25_EMA', '|PC|_25_EMA_13_EMA'], axis=1, inplace=True)
return df
溃疡指数
计算
基于收盘价,溃疡指数根据价格从其高点的贬值来衡量波动性,这是在特定回顾期内。如果价格每个周期都收盘较高,则指数为零。这意味着没有下行风险,因为价格稳步上涨。当然,价格并不会稳步上涨,在这过程中会有下降。使用默认设置的 14 个周期,溃疡指数反映了此期间的预期百分比回撤。表格显示了 14 个周期的样本计算。

Percent-Drawdown = ((Close - 14-period Max Close)/14-period Max Close) x 100
Squared Average = (14-period Sum of Percent-Drawdown Squared)/14
Ulcer Index = Square Root of Squared Average

代码
名称:Ulcer Index
描述:根据收盘价计算溃疡指数
---
代码:
def ulcer_index(df):
df['14-period Max Close'] = df['close'].rolling(window=14).max()
df['Percent-Drawdown'] = ((df['close'] - df['14-period Max Close']) / df['14-period Max Close']) * 100
df['Percent-Drawdown Squared'] = df['Percent-Drawdown'] ** 2
df['Squared Average'] = df['Percent-Drawdown Squared'].rolling(window=14).sum() / 14
df['Ulcer Index'] = df['Squared Average'] ** 0.5
df.drop(['14-period Max Close', 'Percent-Drawdown', 'Percent-Drawdown Squared', 'Squared Average'], axis=1, inplace=True)
return df
终极振荡器
计算
终极振荡器(UO)计算涉及许多步骤。此示例基于默认设置(7,14,28)。首先,计算买入压力(BP)以确定价格走势的总体方向。其次,测量买入压力相对于真实波幅(TR)。这告诉我们收益或损失的真实幅度。第三,基于涉及的三个时间框架(7,14,28)创建平均值。第四,创建三个平均值的加权平均值。
BP = Close - Minimum(Low or Prior Close).
TR = Maximum(High or Prior Close) - Minimum(Low or Prior Close)
Average7 = (7-period BP Sum) / (7-period TR Sum)
Average14 = (14-period BP Sum) / (14-period TR Sum)
Average28 = (28-period BP Sum) / (28-period TR Sum)
UO = 100 x [(4 x Average7)+(2 x Average14)+Average28]/(4+2+1)
买入压力(BP)衡量当前收盘价相对于当前最低价或先前收盘价(以较低者为准)的水平。真实波幅(TR)衡量从当前最高价或先前收盘价(以较高者为准)到当前最低价或先前收盘价(以较低者为准)的价格范围。买入压力和真实波幅都包含先前收盘价,以考虑可能从一个周期到下一个周期的间隙。然后通过将 BP 的 X 周期总和除以 TR 的 X 周期总和来相对于真实波幅显示买入压力。为 7、14 和 28 个周期创建平均值。这些数字对应默认参数。然后通过将最短平均值乘以 4、中间平均值乘以 2 和最长平均值乘以 1 来创建加权平均值。然后将这些加权金额相加,并除以权重之和(4+2+1)。

点击这里")查看 Excel 电子表格中的终极振荡器计算。

代码
# 计算终极振荡器(UO)
def ultimate_oscillator(df):
df['BP'] = df['close'] - df[['low', 'close']].min(axis=1)
df['TR'] = df[['high', 'close']].max(axis=1) - df[['low', 'close']].min(axis=1)
df['BP_sum7'] = df['BP'].rolling(window=7).sum()
df['TR_sum7'] = df['TR'].rolling(window=7).sum()
df['Average7'] = df['BP_sum7'] / df['TR_sum7']
df['BP_sum14'] = df['BP'].rolling(window=14).sum()
df['TR_sum14'] = df['TR'].rolling(window=14).sum()
df['Average14'] = df['BP_sum14'] / df['TR_sum14']
df['BP_sum28'] = df['BP'].rolling(window=28).sum()
df['TR_sum28'] = df['TR'].rolling(window=28).sum()
df['Average28'] = df['BP_sum28'] / df['TR_sum28']
df['UO'] = 100 * ((4 * df['Average7'] + 2 * df['Average14'] + df['Average28']) / (4 + 2 + 1))
return df
涡旋指标
SharpCharts 计算

涡旋指标(VTX)的计算可以分为三部分。首先,根据最近两个周期的高点和低点计算正向和负向趋势运动。正向趋势运动是当前高点到前一低点的距离。当前高点距离前一低点越远,趋势运动越正向。负向趋势运动是当前低点到前一高点的距离。当前低点距离前一高点越远,趋势运动越负向。然后根据指标设置(通常为 14 个周期)对这些周期性值进行求和。
第二部分涉及真实波幅,由 Welles Wilder 创建。该指标使用当前高点、当前低点和前一收盘价来衡量波动性。详情请参见下面的公式框。
第三部分通过将正负趋势运动除以真实波幅来进行标准化。实际上,涡旋指标显示了经过波动调整的正向趋势运动和负向趋势运动。最终结果产生了两个在 1 之上/之下振荡的指标。
Positive and negative trend movement:
+VM = Current High less Prior Low (absolute value)
-VM = Current Low less Prior High (absolute value)
+VM14 = 14-period Sum of +VM
-VM14 = 14-period Sum of -VM
True Range (TR) is the greatest of:
* Current High less current Low
* Current High less previous Close (absolute value)
* Current Low less previous Close (absolute value)
TR14 = 14-period Sum of TR
Normalize the positive and negative trend movements:
+VI14 = +VM14/TR14
-VI14 = -VM14/TR14

上表来自 Excel 电子表格。点击此处下载") 这个电子表格。
代码
名称:涡旋指标(VTX)
描述:根据给定的开盘价、收盘价、最高价和最低价计算涡旋指标(VTX)
代码:
def VTX(df):
df['+VM'] = df['high'].diff().abs()
df['-VM'] = df['low'].diff().abs()
df['+VM14'] = df['+VM'].rolling(window=14).sum()
df['-VM14'] = df['-VM'].rolling(window=14).sum()
df['TR'] = df[['high', 'low', 'close']].apply(lambda x: max(x) - min(x), axis=1)
df['TR14'] = df['TR'].rolling(window=14).sum()
df['+VI14'] = df['+VM14'] / df['TR14']
df['-VI14'] = df['-VM14'] / df['TR14']
return df
威廉斯%R
计算
%R = (Highest High - Close)/(Highest High - Lowest Low) * -100
Lowest Low = lowest low for the look-back period
Highest High = highest high for the look-back period
%R is multiplied by -100 correct the inversion and move the decimal.
威廉斯%R 的默认设置是 14 个周期,可以是天、周、月或日内时间框架。14 个周期的%R 将使用最近的收盘价,过去 14 个周期内的最高价和最低价。

点击这里下载这个电子表格示例。")

代码
# 计算威廉斯%R指标
def williams_r(df, lookback_period=14):
df['Lowest Low'] = df['low'].rolling(window=lookback_period).min()
df['Highest High'] = df['high'].rolling(window=lookback_period).max()
df['%R'] = ((df['Highest High'] - df['close']) / (df['Highest High'] - df['Lowest Low'])) * -100
df.drop(['Lowest Low', 'Highest High'], axis=1, inplace=True)
return df