算法分析与设计
一、算法概述
1.1算法和过程
(1)算法和过程都是解决问题的一种方法的逐步描述
(2) 他们都是由若干条指令组成的有穷序列;每条指令意义确定;具有零个或多个输入;产生若干个输出。
(3) 算法的执行时间是有限的(终止性);过程的执行时间可能是无限的。
1.2算法
(1)程序和算法
① 程序是某个算法 / 过程 在计算机上的具体实现;程序依赖于程序设计语言,甚至依赖于计算机结构。
② 算法是脱离具体的计算机结构和程序设计语言的。
(3)算法的复杂性:算法运行时所需要的计算机资源的量多少。(所需资源量越多则复杂性越高,反之所需资源量越少则复杂性越低)
① 时间复杂性:需要时间的资源量;空间复杂性: 需要空间的资源量。
② 决定算法复杂性的因素:求解问题的规模;具体的输入数据;算法本身的设计。
二、递归和分治
2.1递归
(1)递归概念
① 递归算法 P = if B then Q else β(S, P) 其中,B为递归终止条件,S和Q都不包含P。
② 递归算法的思想:将对较大规模对象的操作归结于对较小规模对象实施同样的操作。
③ 递归元: 递归算法的变元。递归元的变化在递归定义中定义,它的变化能导致递归算法的终止。
(2)汉诺塔问题
void Hanoi(int n, int Fr, int To, int As)
{
if (n > 0) {
Hanoi(n–1, Fro, Ass, To);
Move(Fro, To);
Hanoi(n–1, Ass, To, Fro)}
}
① 汉诺塔问题的时间复杂性为 O(2n)
(3)常见递归形式
-
多变元递归:递归元多于一个的递归
/* 整数划分问题:将一个正整数n表示为一系列正整数之和, n = n1 + n2 +…+nk,其中n1≥n2≥…≥nk≥1, k≥1 (例如ρ(6) = 11,即整数6的划分数为11: 6, 5+1, 4+2, 4+1+1, 3+3, 3+2+1, 3+1+1+1 2+2+2, 2+2+1+1, 2+1+1+1+1, 1+1+1+1+1+1 ) */ q(n, m) { if (n < 1) || (m < 1) return 0; if (n == 1) || (m == 1) return 1; if (n == 1) || (n < m) return 1 + q(n, n–1); return q(n, m–1) + q(n–m, m); } //整数n的划分数ρ(n) = q(n, n) -
多步递归:递归函数f(x, y),其中y是递归元,不仅与f(x, y–1)有关,而且与f(x, y–2),……,乃至f(x, 0)有关。(Fibonacci函数)
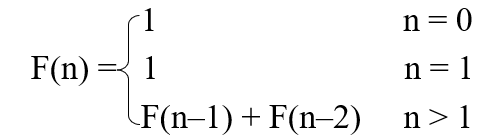
-
嵌套递归:递归调用中又含有递归调用,又称为多重递归

-
联立递归:同时定义几个函数,它们彼此相互调用,从而形成递归,又称间接递归。
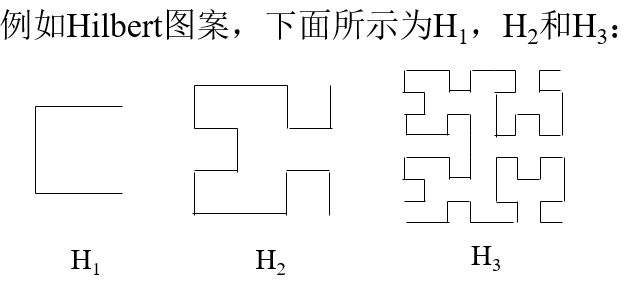
(4)递归算法的时间复杂性
① 递归元的递减方式:减法(n - b)和除法(n / b)
② 递归时间复杂性的递归方程:

③ 当递减方式为 n-- 时,时间复杂性T(n) = O(an)
2.2分治法
(1)分治法
① 分治法基本思想:n将一个规模为n的问题分解为k个规模较小的子问题,这些子问题互相独立且与原问题相同。递归地解这些问题,然后将各个子问题的解合并在一起,从而得到原问题的解。
② 分治法的一般算法模式
Divide-and-Conquer(P)
{//|P|<=n0表示P的规模不超过阈值n0,可直接求解
if (|P|<=n0) return Adhoc(P);
divide P into smaller subinstants P1, .., Pk;
for (i =1; i <= k; i++)
yi = Divide-and-Conquer(Pi);
return Merge(y1, …, yk);
} //算法Merge(y1, …, yk)表示将子问题的解合成P的解
③ 二分搜索的算法复杂度:logn+1;时间复杂度:O( logn )。
④ 分治法复杂度低于原问题,但是整体上能否降低复杂性还取决于合并。通过降低合并复杂性可以降低原问题求解的复杂性。
(2)大整数的乘法
(3)棋盘覆盖问题
三、贪心算法
3.1贪心算法
(1)贪心算法
① 基本思想:贪心算法每次选择目前最优的解,即通过一系列局部最优来获得整体最优。
② 贪心算法的基本要素:贪心选择性质。(指所求问题的整体最优解可以通过一系列局部最优解的选择,即贪心选择来达到。)
③ 贪心算法通常以自顶向下的方式进行,每次贪心选择就将原问题转化为规模更小的子问题。
(2)单源最短路径问题
① 贪心选择策略:选择从源v出发目前用最短的路径所到达的顶点,这就是目前的局部最优解。
② 贪心基本思想:首先设置一个集合S;用数组dis[]来记录v到S中各点的目前最短路径长度。然后不断地用贪心选择来扩充这个集合,并同时记录或修订数组dis[];直至S包含所有V中顶点。
(2.1)Dijkstra算法
① 算法策略:由近到远逐步计算,每次找最近顶点距离作为最短路径长度,然后再从该最近者出发,即依据最近者修订到各顶点距离,再选出新的最近者,直到走完所有顶点。
② 算法举例

③ Dijkstra算法的贪心选择性质:若u是V–S中具有最短路径的特殊顶点,就将u选入S,并确定了从源到u的最短路径长度D[u]。
④ Dijkstra算法的时间复杂度:O(n2)。因为他有两层循环,外层循环n次,内层的两个循环一个是选出最小距离,一个是修订距离数组,他们次数都是n/2,所以时间复杂度为O(n2)。
3.2最小生成树问题
(1)Prim 算法
① 基本思想:在保证连通的前提下依次选出权重较小的n – 1条边(在实现中体现为n个顶点的选择)。
(下图中T为G的最小生成树)

② 算法中的数据结构:
- 用连接矩阵C[ i ] [ j ] 表示图,Cn [ i ] [ j ] 为结点 i 到 j 权重。
- 对图中每个顶点设两个数组 closest [ j ] 和 lowcost [ j ] :closest [ j ] 是 s 中与 j 最近的顶点,即为选中的边; lowcost [ j ] 是相应边的权重。
③ 算法实现
Prim(int n, Type **c) {
int j = 1; s[j] = true;
for(int i = 2; i <= n; i++) {
closest[i] = 1;
lowcost[i] = c[1][i];
s[i] = false;
}
for(int i = 1; i < n; i++) {
min = inf;
for(int k = 2; k <= n; k++) {
if(lowcost[k] < min && !s[k]) {
min = lowcost[k];
j = k;
}
s[j] = true;
for(int k = 2; k <= n; k++) {
if(c[j][k] < lowcost[k] && !s[k]){
lowcost[k] = c[j][k];
closest[k] = j;
}
}
}
④ 算法示例
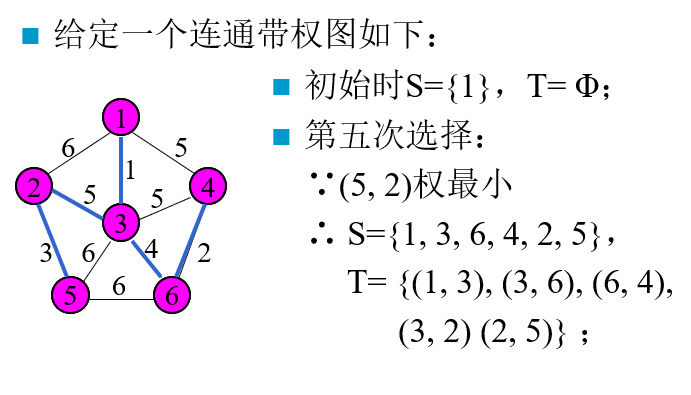
(2)Kruskal算法
①基本思想:在保证无回路的前提下依次选择权重较小的n – 1条边。

② 算法中的数据结构:
- 数组 e [ ] [ ] 表示图的边。e [ i ] [ u ] ,e [ i ] [ v ] 表示边 i 的两个端点,e [ i ] [ w ] 表示边 i 的权重。
- 使用 sort() 函数将数组按权重 w 从小到大排列。
- 使用 initialize(n) 初始化;find(u) 找顶点所在集合;union(a,b) 合并集合a,b ;重载 != 判断集合是否相等。
③ 算法举例
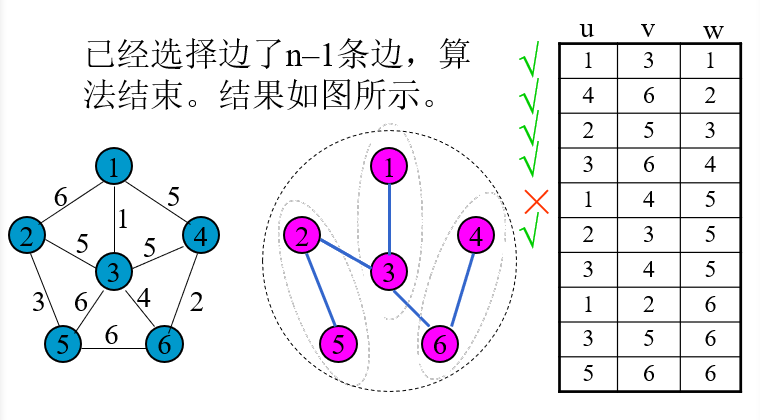
(3)对比 Prim算法 和 Kruskal算法
① Prim算法为两重循环,外层循环n次,内层循环O(n),所以复杂性为O(n2) 。
② Kruskal算法中,设边数为e,则边排序的时间为O(e),确定边的时间为O(loge),所以整个时间复杂性为O(eloge)。
③ 点比边多时,用Kruskal算法更好,反之用Prim。
(4)用Kruskal算法得到的生成树T*必是最优树。
标签:总结,递归,int,复杂性,学习,算法,顶点,贪心 From: https://www.cnblogs.com/robber-is-best/p/17976785