人工智能
四、线性回归
4.1 线性回归

(1)线性回归特点:解释性强,简单,泛化能力稳定。
(2)特征 : 输入的不同维度叫做特征。如果特征本身很重要,线性回归就很有效,但是挑选特征是非常困难的。(神经网络本质就是自动挑选、学习特征的机器)
(3)最小化损失函数的方法:梯度下降法
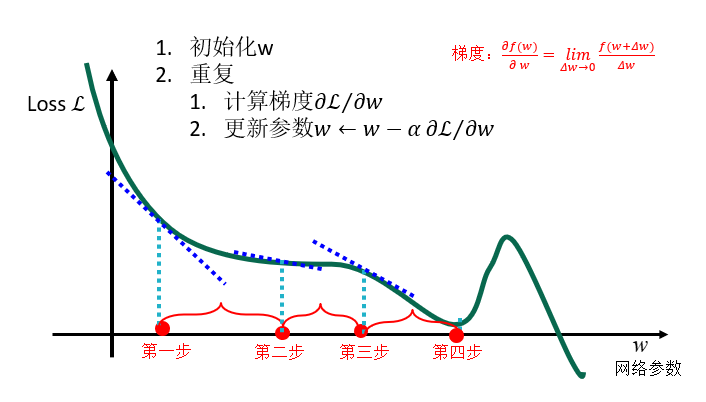
梯度下降法的计算
4.2 感知算法
(1)感知算法是神经网络原始形式;只能够学线性可分的函数
(2)逻辑回归——二分类: f ( x ) = 在A类别的概率;1 - f ( x ) = 在B类别的概率
(3)逻辑回归——决策分界:sign ( wT x ) 的 “ 软化 ” 版本。
(4)多分类问题:与二分类问题相似,不过在其基础上添加了一个概率。不仅适用于线性问题,也适用于神经网络及其他多分类问题。(使用了softmax函数,即sigmoid函数的更一般形式)
4.3 熵
(1)信息熵

(2)交叉熵:主观上认为一个事情发生的概率很低(1/ ps(x) 很大),但客观上发生概率很高(po(x) 很大)时,交叉熵很大。
① XE(y, p) = - Σi yi log pi
② 主观客观匹配时,交叉熵 = 信息熵
③ 比使用 log yi 编码效率低,所以 XE(y, p) ≥ H(y)
(3)相对熵,KL散度:度量主观认识和客观之间的差异
(4)岭回归
① 本质是 线性回归 + 控制参数长度
② 虽然参数向量长度会短一些,但每个特征仍会得到一些(可能非常小的)系数

(5)套索回归:寻找稀疏解
① 使用 1- 范数 (矩形)
② 优化:将每步梯度下降分为两部分(本质是拖到0),一直重复这两部分,直到两部分对冲,形成均衡。
(6)比较线性回归,岭回归,套索回归:线性回归的答案可以完美拟合最后的问题,岭回归给出的答案有更小的长度,套索给出的答案更加稀疏(第二个维度是0)。
4.4 支持向量机(SVM)
(1)硬边界 和 软边界
① 硬边界:特征最多在边界上。
② 软边界: “稍微越界了一点” 没问题。
(2)SVM-硬边界版本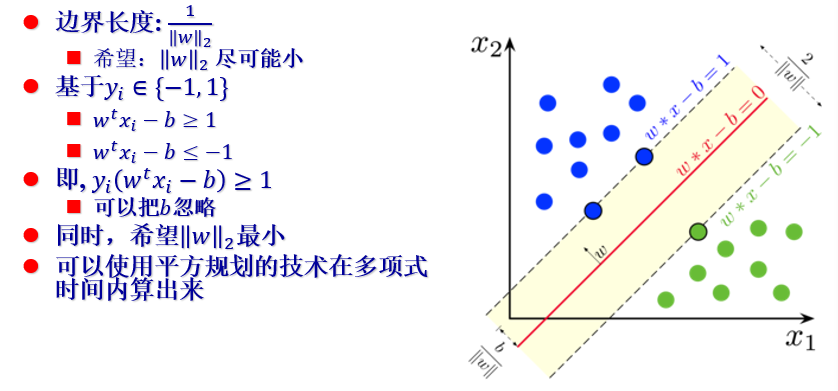
(3)核方法:将数据变换到另一个线性可分的空间。(使用核函数)
① 适用场景:不存在一个能正确划分两类样本的超平面时,使用核函数将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。
② 问题:核函数维度过高,很难计算;分类器维度过高,很难计算。
五、决策树
5.1 决策树模型
(1)定义
① 决策树适用于表格数据——特征既有类别特征也有数值特征
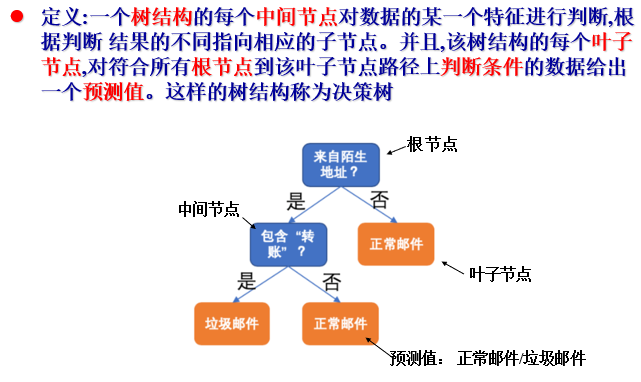
② 决策变量和目标
- 决策变量:特征 X(是否来自陌生地址、是否包含 “转账” …)
- 决策目标:预测值Y(回归问题,如预测目标是实数,如价格;分类问题,如预测目标是正常、垃圾邮件)
③ 决策树表示一个分段常数函数(将输入的数据X所在空间分割为多个不同子空间,然后为每个子空间(对应一个叶子节点)赋予一个预测值)
④ 特点:模型相对简单,具有较好的解释性,但是预测效果比不上更高级的模型
⑤ 使用了自顶向下的构造算法
5.2 决策树的训练
(1)决策树的组成:叶子节点的预测值+决策树的结构。
(2) 决策树训练:产生一棵泛化能力强的决策树,通过特征逐级判断,从根节点——叶子赋值未见示例。
① 初始化一根节点,对应所有训练数据。
② 选择一个特征,设置一个分割条件。
③ 依据该条件构造根的两个叶子,每个叶子对应一部分数据。
④ 重复以上步骤至达到一定的终止条件。
根据损失函数易求出每片叶子上的最优预测值。
(3)划分选择
① 决策树学习的关键:如何选择最优划分属性。(一般希望决策树分支结点所包含样本尽可能属于同一类别,即结点 “纯度” 越来越高)
② 经典属性划分方法:信息增益、增益率、基尼指数。
③ 信息增益:信息增益越大,使用属性 a 来进行划分所获得的 “纯度提升”越大。(ID3 决策树学习算法以信息增益为准测来选择划分属性)
信息增益的计算
(4)基尼指数:
① 基尼值:反映了从D中随机抽取两个样本,其类别标记不一致的概率。用于度量数据集D的纯度,基尼值越小数据集D纯度越高。
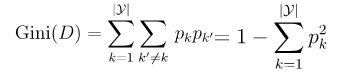
②数据集D中属性a的基尼指数:
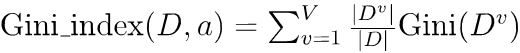
③ 应选择使划分后基尼指数最小的属性作为最优化分属性。(CART采用“基尼指数”来选择划分属性,以减少对数运算)
(5)剪枝
① 预剪枝:在决策树的训练过程中加入限制条件, 避免违反这些限制条件的分割
② 后剪枝:先训练一个规模足够大的决策树, 然后再删去多余的树分支
六、集成学习
6.1 集成学习
(1)集成学习思想: 集合一系列弱模型的预测结果,从而实现更稳定、表现更好的模型。
(2)集成方法
① 平行的集成学习方法:引导聚集方法(随机森林)
② 串行的集成学习方法:提升算法(梯度提升决策树)
6.2 随机森林
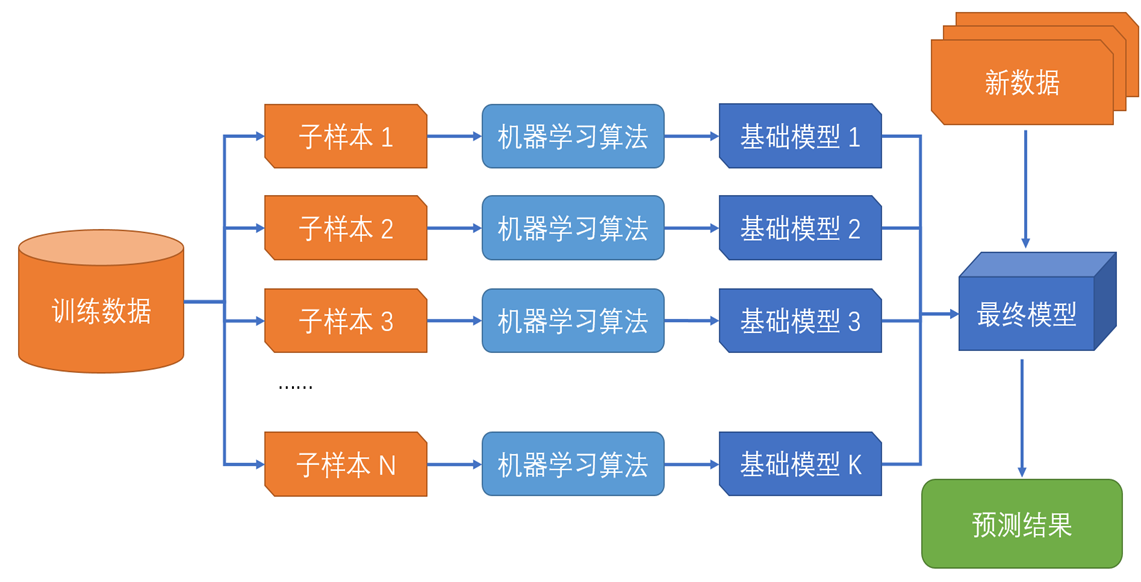
(1)思想:训练多个决策树,在训练每个决策树时引入一定的随机性(避免在训练中多个决策树给出相同的预测)
(2)决策树训练
① 在训练时随机选取训练数据的一部分进行训练,而不是训练全部数据。(选取80%训练数据训练)
③ 决策树训练中分割叶节点时随机选取特征的一个子集,仅从该子集中选取最优分割条件
(3)预测
- 回归问题:预测输出为所有决策树预测的均值
- 分类问题:对所有决策树预测类别进行投票,取得票最高类别作为最终预测结果
(4)特点
① 随机性:训练数据的随机性;特征选取的随机性(分割叶子节点时仅考虑随机选取的两个特征)
② 限制决策树最大深度为1,不同子树相对独立
③ 适用于表格型数据
(5)优缺点
① 利用随机性在同一训练集上训练出多个不同的决策树,整合这些决策树的结果达到超过单个决策树的效果;模型效果一般比较好;训练速度比较慢(相对GDBT模型)。
6.3 梯度提升
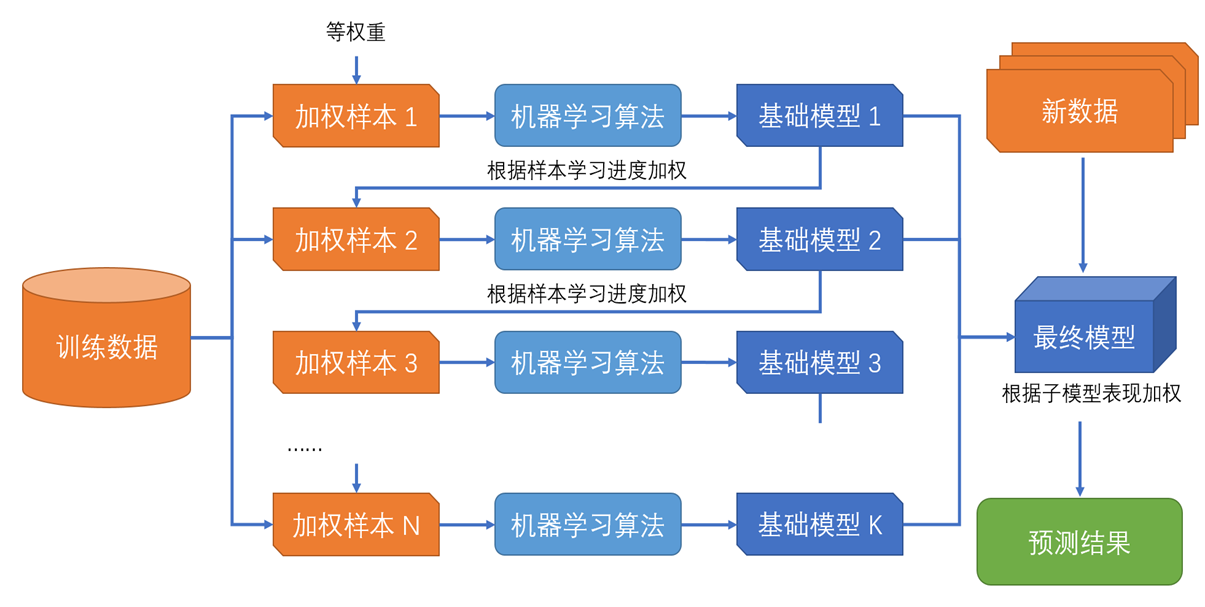
(1)思想:不断训练新的决策树,以弥补已经训练好的决策树的误差。
(2)特点
① 梯度提升使用的子模型通常是决策树这样的简单模型
② 广泛应用于表格类数据,使用非常广泛
③ 新子树拟合已有子模型的结果相对于数据标签的残差或负梯度,字数间不独立
(3)防止过拟合:在第n + 1 轮损失函数中加入正则项Ω(T(n+1)) 来表示决策树Tn+1的复杂度。
(2)梯度提升决策树和随机森林相比:梯度提升决策树各个子模型之间存在更强的依赖关系。
标签:总结,基尼,训练,人工智能,回归,学习,特征,线性,决策树 From: https://www.cnblogs.com/robber-is-best/p/17976786