人工智能

一、人工智能绪论、基础

（1）人工智能、基因工程、纳米科学被认为是21世纪的三大尖端技术。

（2）人工智能的典型应用领域：交通、服务机器人、医疗健康、教育、公共安全、工作就业、娱乐。

二、搜索

（1）单智能体搜素：规划

• 盲目搜索
• 启发式搜索
• 局部搜索

（2）多智能体搜索：零和博弈

• 极大极小搜索
• Alpha-Beta剪枝搜索

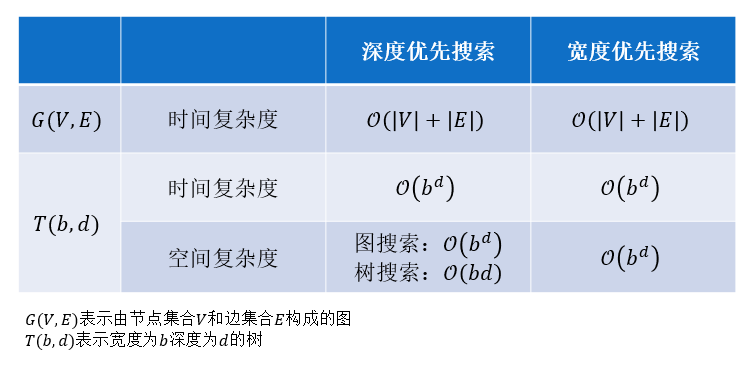
2.1无信息搜素（盲目搜索）：

（1）相关术语

（2）没有先验知识，按照事先确定的排序搜索。

​ ① 深度优先搜索：优先选择当前能够到达最深的节点（栈）

​ ② 宽度优先搜索：优先选择当前能够到达最浅的节点（队列）

2.2有信息搜索：启发式搜索。

​ （1） 贪婪搜索：选择当前代价估计最小的节点，用优先队列存储候选节点。

​ （2）A* 搜索：选择当前代价估计 f 值最小的节点，用优先队列存储候选节点。

​ ① f (s) = g(s) + h(s)

​ ② 实际代价函数 g(s)：起始节点到达节点s的代价值

2.3局部搜索

（1）简介

​ ① 用于处理 “ 只关心算法返回状态是否达到目标而非其到达目标路径” 的问题。

​ ② 优点： 不需要维护搜索树；占用内存小（不用存储路径）；在连续且状态空间很大的问题通常都可以找到足够好的解；以时间换精度。

（2）k-opt 算法

​ ① 局部最优搜索算法，常见的有 2-opt，3-opt，k-opt。

​ ② 2-opt 算法：核心在于随机选择一个区间段优化，优化只是针对当前状态而非全局。

​ ③ 算法步骤：

​ 参考链接：[2-opt算法]写给媳妇儿的算法（二）——2-opt算法解决商旅问题 - 简书 (jianshu.com)：

​ ④ 优缺点： 简单灵活，易于实现；容易陷入局部最优而无法达到全局最优，解的质量与最初解的选择和领域结构密切相关。

（3）爬山法

① 一种局部择优的贪心搜索算法，本质是梯度下降法， 核心是不断移动至邻域内最优点。

② 算法问题：容易陷入局部最优解；高地问题—搜索到达高地后无法确定搜素最佳方向，会产生随机走动使得效率降低；山脊问题—搜索可能在山脊两面来回震荡使得前进步伐很小。

③ 算法优势：避免了遍历全部节点；需要多次随机初始化后返回评估值最优的解，达成效率与最优性的平衡。

④ 结合爬山法和随机游走有概率摆脱局部最优。

（4）模拟退火法

① 用温度控制搜索的随机程度：温度高能量大，粒子行为活跃，选择下一个状态的策略更接近随机游走；温度低能量下降，粒子热运动减弱，选择策略更倾向选择更优。

② 算法伪码

（5）遗传算法

① 实现对最优化问题解的参数空间进行高效搜索。

② a. 种群中每个个体即一个解（不一定最优），个体的编码成为基因型。

​ b. 选择种群中部分个体来培育下一代种群。（通过交叉过程）

​ c. 适应度函数：用来衡量种群中每个个体的优劣程度（适应度越高越容易被选中）

​ d. 变异：在种群演化中引入一定多样性，使基因型有一微小概率产生随机变化。

2.4 对抗搜索

（1）简介

​ ① 相关术语

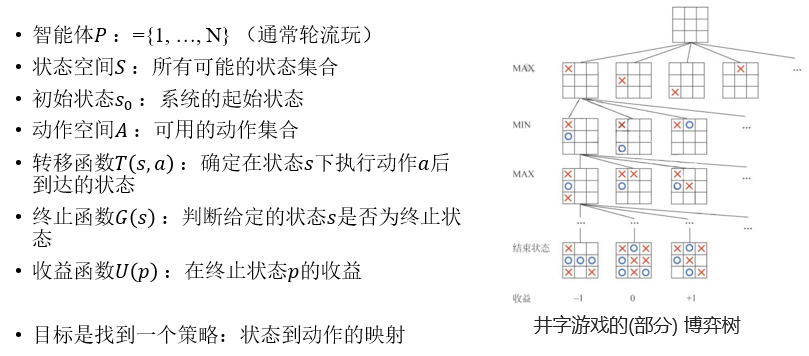
​ ② 两个智能体的零和博弈：双方收益的和为零，即必有一方获胜或双方打平的博弈。（围棋、国际象棋、猜拳游戏…）

​ ③ 博弈树：由初始状态 s₀ 、动作集合 A 、收益函数 U(p) 生成。节点表示博弈的一个状态，叶节点表示博弈结果。收益函数确定博弈结束双方的胜负情况。

（2）极大极小搜索

​ ① 使用极小极大搜索算法在博弈树中递归求解时,两位玩家分别交替使用使收益极小和极大的动作。

​ ② 算法伪码：

​ ③ 算法优缺点：能找到最优策略；需要展开整个搜索树，对大部分问题而言不可行，搜索树太大了。

（3）Alpha-Beta剪枝搜索

​ ① 基本思想：如果当前节点已知对手存在一策略可使自己收益减少，则玩家一定不会选择该节点，故无需继续搜索该节点后续节点，被称为 “剪枝”。

​ ② 引入两变量，Alpha 表示MAX玩家当前最优值，Beta 表示 MIN玩家当前最优值，若某节点 Alpha >= Beta，说明该玩家当前最优策略（Beta）劣于之前已有最优策略（Alpha），进行剪枝。

​ ③ 算法伪码

（4）蒙特卡洛树搜索（Monte Carlo Tree Search，MCTS）

​ ① 一种概率和启发式驱动的搜索算法，结合了经典的树搜索实现和强化学习的机器学习原理。

​ ② 主要步骤

• 选择：目标是找到没有被搜索过的叶节点，具体规则由多项式上置信树算法（PUCT）决定。（该算法会根据算式给每个子节点算分，不断递归选择分数最高节点至到达一个叶节点）

  ​ 节点选择规则（Upper Confidence Boundary, UCB）：

  

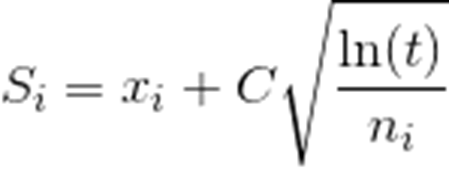
• 拓展：将新的子节点加入树

• 模拟：新结点用快速走子策略走到底，得到一个胜负结果。（按照普遍的观点，快速走子策略适合选择一个棋力很弱但走子很快的策略）

• 回溯：把模拟结果加到它的所有父节点上。

• 最后的决策

三、机器学习

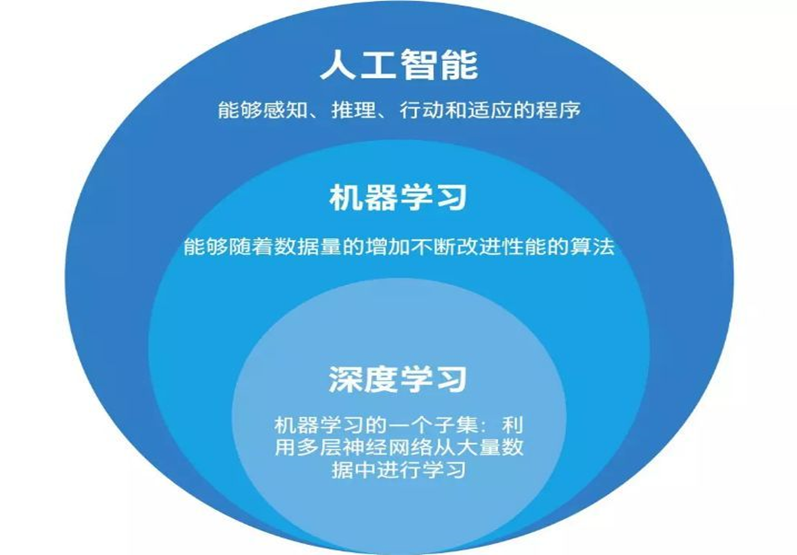
（1）人工智能 > 机器学习 > 深度学习

3.1 监督学习

​ （1）机器学习的重要分支，本质上是根据数据中的例子进行学习：

​

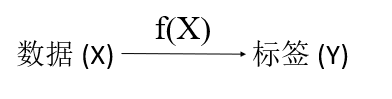
​ 想要使函数 f ( x _i ) ≈ y _i ：约等号是由于严格等于有时候是不可能的；y 可能包含噪声。

​ （2）监督学习目标：找到一个好的 f 。使用优化寻找 ， f 应具有好的泛化性。

​ ① 确保好的泛化性的方法：调优。（将训练数据集分成训练集+调优集。用训练集来找 f ,用调优集来测试）

​ ② 交叉调优

（3）监督学习框架

​ ① 确认目标问题

​ ② 创建数据集（包含成千上万的输入输出数据点 x_i ，y_i ）

​ ③ 针对问题选择一个好的机器学习模型 f

​ ④ 定义一合适的损失函数 L 度量 f (X) 和 Y 的距离

​ ⑤ 以损失函数为指标，使用优化算法寻找 f 的参数组合

​ ⑥ 确定 f 具有好的泛化性

（4）其他相关概念

（5）过拟合和欠拟合

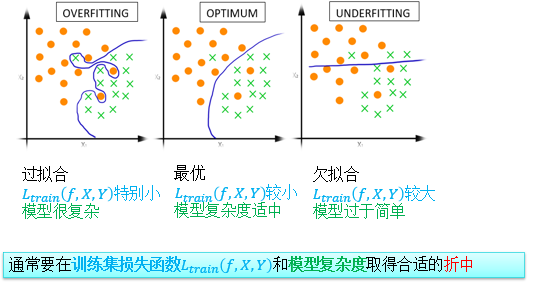
​ ① 过拟合： 函数表达能力太强；过拟合很容易使训练损失L _train ≈ 0；泛化问题中测试损失 L _test 可能很差（但是几乎从来没有发生过）。

​ ② 欠拟合： 函数表达能力不足；欠拟合给出一个很差的训练损失L _train ； 一般没有泛化问题，因为 L _test 同样差。

（6）无监督学习和半监督学习

​ ① 无监督学习：只有输入数据X，没有标签。（用于聚类、PCA、生成模型、异常检测、数据降维…）

​ ② 半监督模型： 只有一小部分数据有标签，其他的没有标签。

​ ③ 聚类： 把数据点分类，同一类的数据比较相似；形式分为聚合型、连通类聚类；没有唯一的解法（和损失函数密切相关）。（用于数据挖掘与数据分析、加速优化过程、推荐系统…）

（7）K means 聚类算法

​ ① 算法步骤

• 确定好 k
• 随机选择 k 个中心
• 将每个点与离他最近的中心相连
• 将每个聚类的点求平均算作新的中心
• 重复 3、4步直到收敛

​ ② 算法一定会收敛的原因： 每个点到自己聚类中心的平均位置随着每一步迭代优化都在不断下降；n 个点分成 k 类分类方法有限。