介绍
线性判别分析(Linear Discriminant Analysis, LDA)是一种有监督式的数据降维方法,是在机器学习和数据挖掘中一种广泛使用的经典算法。
LDA的希望将带上标签的数据(点),通过投影的方法,投影到维度更低的空间中,使得投影后的点,按类别区分成一簇一簇的情况,并且相同类别的点,将会在投影后的空间中更接近。

如上图所示(数据只有二维的情况),LDA希望能寻找到第二条直线,并将高维的数据投影到低维空间中,使得类之间耦合度低,类内的聚合度高。这样的话,接下来就可以方便利用低维的数据对数据进行分类。
理论基础
见: https://leondong1993.github.io/2017/05/lda/ 讲解比较清楚!
核心就是求解一个n*k矩阵将原来n维的数据降到k维,也就是说把原始数据降低到了k维。
一个简单的例子
假设我现在有两类数据,如下图所示。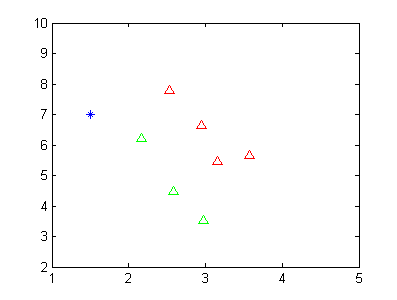
其中红色的三角形代表一类数据,绿色的三角形代表第二类数据。蓝色的点代表未知样本点,我想通过LDA的方式判断其类别。当然从这个二维图中,我们可以看到该蓝色的数据点应该是属于第二类的(绿色)。
LDA得到两类数据的一维表示,如下图所示。
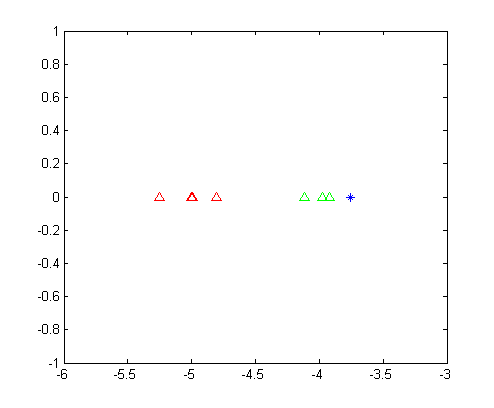
从这幅图里面我们可以清晰的看出,第一类数据和第二类数据被完美的分开了,并且可以明显的看出来,位置数据应该是属于第二类的。
代码参考:
import numpy as np
### 定义LDA类
class LDA:
def __init__(self):
# 初始化权重矩阵
self.w = None
# 协方差矩阵计算方法
def calc_cov(self, X, Y=None):
m = X.shape[0]
# 数据标准化
X = (X - np.mean(X, axis=0))/np.std(X, axis=0)
Y = X if Y == None else \
(Y - np.mean(Y, axis=0))/np.std(Y, axis=0)
return 1 / m * np.matmul(X.T, Y)
# 数据投影方法
def project(self, X, y):
# LDA拟合获取模型权重
self.fit(X, y)
# 数据投影
X_projection = X.dot(self.w)
return X_projection
# LDA拟合方法
def fit(self, X, y):
# (1) 按类分组
X0 = X[y == 0]
X1 = X[y == 1]
# (2) 分别计算两类数据自变量的协方差矩阵
sigma0 = self.calc_cov(X0)
sigma1 = self.calc_cov(X1)
# (3) 计算类内散度矩阵
Sw = sigma0 + sigma1
# (4) 分别计算两类数据自变量的均值和差
u0, u1 = np.mean(X0, axis=0), np.mean(X1, axis=0)
mean_diff = np.atleast_1d(u0 - u1)
# (5) 对类内散度矩阵进行奇异值分解
U, S, V = np.linalg.svd(Sw)
# (6) 计算类内散度矩阵的逆
Sw_ = np.dot(np.dot(V.T, np.linalg.pinv(np.diag(S))), U.T)
# (7) 计算w
self.w = Sw_.dot(mean_diff)
# LDA分类预测
def predict(self, X):
# 初始化预测结果为空列表
y_pred = []
# 遍历待预测样本
for x_i in X:
# 模型预测
h = x_i.dot(self.w)
y = 1 * (h < 0)
y_pred.append(y)
return y_pred
# 导入LinearDiscriminantAnalysis模块
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# 导入相关库
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 导入iris数据集
data = datasets.load_iris()
# 数据与标签
X, y = data.data, data.target
# 取标签不为2的数据
X = X[y != 2]
y = y[y != 2]
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=41)
# 创建LDA模型实例
lda = LDA()
# LDA模型拟合
lda.fit(X_train, y_train)
# LDA模型预测
y_pred = lda.predict(X_test)
# 测试集上的分类准确率
acc = accuracy_score(y_test, y_pred)
print("Accuracy of NumPy LDA:", acc)
# 创建LDA分类器
clf = LinearDiscriminantAnalysis()
# 模型拟合
clf.fit(X_train, y_train)
# 模型预测
y_pred = clf.predict(X_test)
# 测试集上的分类准确率
acc = accuracy_score(y_test, y_pred)
print("Accuracy of Sklearn LDA:", acc)
好难!还有一些实现:
https://python-course.eu/machine-learning/linear-discriminant-analysis-in-python.php
https://www.adeveloperdiary.com/data-science/machine-learning/linear-discriminant-analysis-from-theory-to-code/
import numpy as np
import matplotlib.pyplot as plt
from sklearn import preprocessing
import seaborn as sns
def load_data(cols, load_all=False, head=False):
iris = sns.load_dataset("iris")
if not load_all:
if head:
iris = iris.head(100)
else:
iris = iris.tail(100)
le = preprocessing.LabelEncoder()
y = le.fit_transform(iris["species"])
X = iris.drop(["species"], axis=1)
if len(cols) > 0:
X = X[cols]
return X.values, y
class LDA:
def __init__(self):
pass
def fit(self, X, y):
target_classes = np.unique(y)
mean_vectors = []
for cls in target_classes:
mean_vectors.append(np.mean(X[y == cls], axis=0))
if len(target_classes) < 3:
mu1_mu2 = (mean_vectors[0] - mean_vectors[1]).reshape(1, X.shape[1])
B = np.dot(mu1_mu2.T, mu1_mu2)
else:
data_mean = np.mean(X, axis=0).reshape(1, X.shape[1])
B = np.zeros((X.shape[1], X.shape[1]))
for i, mean_vec in enumerate(mean_vectors):
n = X[y == i].shape[0]
mean_vec = mean_vec.reshape(1, X.shape[1])
mu1_mu2 = mean_vec - data_mean
B += n * np.dot(mu1_mu2.T, mu1_mu2)
s_matrix = []
for cls, mean in enumerate(mean_vectors):
Si = np.zeros((X.shape[1], X.shape[1]))
for row in X[y == cls]:
t = (row - mean).reshape(1, X.shape[1])
Si += np.dot(t.T, t)
s_matrix.append(Si)
S = np.zeros((X.shape[1], X.shape[1]))
for s_i in s_matrix:
S += s_i
S_inv = np.linalg.inv(S)
S_inv_B = S_inv.dot(B)
eig_vals, eig_vecs = np.linalg.eig(S_inv_B)
idx = eig_vals.argsort()[::-1]
eig_vals = eig_vals[idx]
eig_vecs = eig_vecs[:, idx]
return eig_vecs
# Experiment 1
# cols = ["petal_length", "petal_width"]
# X, y = load_data(cols, load_all=False, head=True)
# print(X.shape)
# lda = LDA()
# eig_vecs = lda.fit(X, y)
# W = eig_vecs[:, :1]
# colors = ['red', 'green', 'blue']
# fig, ax = plt.subplots(figsize=(10, 8))
# for point, pred in zip(X, y):
# ax.scatter(point[0], point[1], color=colors[pred], alpha=0.3)
# proj = (np.dot(point, W) * W) / np.dot(W.T, W)
# ax.scatter(proj[0], proj[1], color=colors[pred], alpha=0.3)
# plt.show()
# Experiment 2
# cols = ["petal_length", "petal_width"]
# X, y = load_data(cols, load_all=True, head=True)
# print(X.shape)
# lda = LDA()
# eig_vecs = lda.fit(X, y)
# W = eig_vecs[:, :1]
# colors = ['red', 'green', 'blue']
# fig, ax = plt.subplots(figsize=(10, 8))
# for point, pred in zip(X, y):
# ax.scatter(point[0], point[1], color=colors[pred], alpha=0.3)
# proj = (np.dot(point, W) * W) / np.dot(W.T, W)
# ax.scatter(proj[0], proj[1], color=colors[pred], alpha=0.3)
# plt.show()
# Experiment 3
X, y = load_data([], load_all=True, head=True)
print(X.shape)
lda = LDA()
eig_vecs = lda.fit(X, y)
W = eig_vecs[:, :2]
transformed = X.dot(W)
plt.scatter(transformed[:, 0], transformed[:, 1], c=y, cmap=plt.cm.Set1)
plt.show()
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
clf = LinearDiscriminantAnalysis()
clf.fit(X, y)
transformed = clf.transform(X)
plt.scatter(transformed[:, 0], transformed[:, 1], c=y, cmap=plt.cm.Set1)
plt.show()
标签:LDA,self,判别分析,shape,算法,eig,np,mean From: https://www.cnblogs.com/bonelee/p/17688826.html