- 写在前面
这两个东西其实并没有什么联系,但是因为都是由 @dd_d 首创的,所以写在一起。
Update:不想新开博客了,所以以后 dd_d 有什么新发明就直接在这里更新了。
-
港队线段树
这是一种高效且简便好写的优秀线段树( 由香港队长发明的 ),拥有良好的均摊复杂度。
在同时需要记录多个标记时,有十分简洁的下传方式,甚至无需标记( 与标记永久化类似思想,但不完全相同 )。
实现原理则是充分利用了线段树叶子节点的性质,使其能快速合并信息。
其实港队线段树不难理解,如果你学过线段树,看代码就能完全理解,但是从古至今却只有他一个人想到了这种高妙的办法。
大致算法流程( 用修改举例,其他同理 )
void update(...) {
if(The length of the section is only 1) {
//Edit the value
...
return ;
}
//push_down(...);
if(Can reach the left section) update(The left son);
if(Can reach the right section) update(The right son);
}
当遇到实际题目时,如果能充分利用叶子节点的性质,一些情况下可以使码量大大减小,对港队来说 push_down 只是画蛇添足!
- 举个例子:[清华集训2012]序列操作
按照题解思路将式子展开以后,其他操作可以直接套用港队线段树。
询问只需要按照推出来的式子,预处理一下组合数,从叶子向上乘起来即可,式子不写了,可以去题解区看,会比好写很多,且变得完全没有思维难度了。
- 有同学可能会问:为什么复杂度是对的呢?
考虑当询问一定会分为多个区间,参考下图
这些区间上的存储值合并后就是答案。
考虑这些区间的长度有长有短,在询问随机情况下,我们也许只要 \(1\) 个就能获得答案,也许 \(\log(n)\) 次就会获得答案。
仔细推理一下或感性理解一下就能发现,均摊复杂度为单次 \(O(\log n)\)。
至于修改操作,在较好的随机情况下是 \(O(\sqrt{n})\) 级别的,不算很劣,如果仔细的研究数据规模后,可以在比较好条件下达到 \(O(\log(n))\) 甚至 \(O(1)\)。
但是在方便的前提下谁会在意复杂度呢
-
马表
这个目前还在理论阶段,没有比较优秀的实践价值。
马表,即为带修 st 表,最基础的马表支持期望 \(O(\log n)\) 单点修改,\(O(k)\) 求区间 RMQ,\(k\) 为一个常数,一般的马表 \(k\) 期望为 \(4\sim5\),优秀的可达到 \(2.64\) 左右大小。
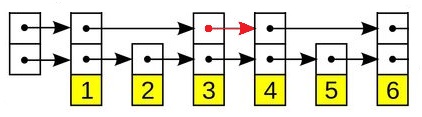
思路就是借用一个 Skip List 的分层概念,修改会在表上多开一个节点,节点过多就重复利用,使节点数控制在一定范围内,查询就在每层上查询。
可以参考图片理解,红色箭头表示一次修改。
相比线段树,马表就有很大优化空间,修改时一些点可以只先在高层打标记,询问时下传到下层,实测所用时间比线段树的 \(\frac{1}{2}\) 还略快。
并且 st 表能维护的内容马表都能维护,并且可以可持久化,十分优秀。
-
ex马表
带修带插入的马表,在马表基础上再倍增分块,插入在最顶层,查询再向下新建,小块暴力修改,过大后暴力 split。
但是 \(k\) 能被卡的非常大,可以搞一个估价函数,为块数在再乘一个指数函数,通常取 \((\sqrt{2})^x\),超过一定之后层与层之间 shuffle 一下,再重建层与层之间的边,在随机数据下跑的飞快。
先考虑插入的每个数字大小和位置都是随机的,即随机到每一块的概率是 \(O(\log n)\) 的,也就是说,期望 \(O(\log^2 n)\) 次会有 \(\frac{\log_2 n}{\log_k n}\) 次 split( \(k\) 是期望层数 ),因此 split 的总复杂度为 \(O(\frac{q}{\log_k n})\),不会对马表总复杂度产生影响。
然后是重构,由 split 平衡后,至少要 \(\log n\times tn\) 次才会重构,\(t\) 取决于估价函数的优劣,大概是 \(0.23\sim0.61\)。总复杂度为\(\frac{q}{\log n\times tn}\times n\log n\),为 \(O(\frac{q}{t})\),上限约为 \(O(4.236\times q)\),同样小于朴素马表。
做法似乎十分暴力,但复杂度同样正确。
删除也可以按照这个思路,块内少了就 merge,不平衡就重构,复杂度同理。
ex马表也同马表一样,st 表能维护的都能维护。
- 马表的其他用处
马表可用范围很广,能套用其他数据结构,可以在马表上倍增,或是用马表优化建图,但由于还是理论数据结构,这里就不展开了。
-
港队矩乘
先占坑,以后在写。
- 特别鸣谢 @Freedom_King 的帮助和支持。