五、证明:在过程 PERMUTE-BY-SORTING的数组 P中，所有元素都唯一的概率至少是1-1/n。

文心一言：

证明：

在过程PERMUTE-BY-SORTING中，对于输入数组P中的每个元素，其出现次数为1，因此对于每个元素，在排序后的数组中，它出现的位置是唯一的。

假设在排序后的数组中，有两个元素a和b，它们在原始数组P中的位置分别为i和j，且i eq j。由于排序是稳定的，因此在排序后的数组中，a和b仍然会分别出现在它们在原始数组中的位置。因此，如果存在两个不同的元素在排序后的数组中具有相同的值，则它们在原始数组中的位置必定不同。

由于在原始数组中，每个元素的出现次数为1，因此在排序后的数组中，每个元素在排序后出现的次数也为1。因此，如果两个不同的元素在排序后的数组中具有相同的值，则在原始数组中它们的出现位置也必定不同。

因此，在过程PERMUTE-BY-SORTING中，对于输入数组P中的每个元素，在排序后的数组中，它出现的位置是唯一的。由于每个元素的出现次数为1，因此所有元素都唯一的概率至少是1-1/n。

讯飞星火：

【详解】

设$P_{i}$为排列$\left{ P_{1}{,}P_{2}{,\cdots ,}P_{n}\right}$中，所有元素都唯一的概率。

当$n{=}2^{k}$时，在数组$P_{1}{,}P_{2}{,\cdots ,}P_{n}$中，任取两个不同的元素$P_{i}{、}P_{j}$,则由乘法原理知，其组合数为$C_{n}^{2}{=}C_{2k2}{=}\dfrac{2k(2k{-}1)}{2}{=}k(2k{-}1)$.

若这两个元素在数组$P_{1}{,}P_{2}{,\cdots ,}P_{n}$中不唯一，则它们必有公共元素$P_{m}$.从而，这两个元素的全排列个数为$A_{m}^{2}$.

于是，由加法原理得$\sum\limits_{i{< }j{< }}^{n}{(i{< }j)}{=}\sum\limits_{i{< }j{< }}^{2k}{(i{< }j)}{=}\sum\limits_{i{=}12k}{C_{2k}^{i{-}1}{\cdot }(i{-}1){=}\sum\limits_{i{=}12k}{(i{-}1){\cdot }C_{2k}^{i{-}1}}}$

${=}(0{+}1{+}2{+}\cdots {+}2k{-}1){\cdot }\sum\limits_{i{=}1}^{2k}{C_{2ki{-}1}{=}(0{+}1{+}2{+}\cdots {+}2k{-}1)}{\cdot }\dfrac{1}{2}{\cdot }(1{+}2k{-}1){\cdot }(2k{-}1)!{=}(2k{-}1)(2k)!$.

所以，$P_{i}{、}P_{j}$不唯一的概率为$\dfrac{(2k{-}1)(2k)!}{k(2k{-}1)}{=}(2k{-}1)!$.

因此，$P_{i}$为排列$\left{ P_{1}{,}P_{2}{,\cdots ,}P_{n}\right}$中，所有元素都唯一的概率为$1{-}[(n{-}1)!]$.

当$n{=}3^{t}$时，在数组$P_{1}{,}P_{2}{,\cdots ,}P_{n}$中，任取三个不同的元素$P_{i}{、}P_{j}{、}P_{r}$,则由乘法原理知，其组合数为$C_{\mathrm{3}^{{\mathrm{t}}3}{=}3}{\mathrm{t}}$.

若这三个元素在数组$P_{1}{,}P_{2}{,\cdots ,}P_{n}$中不唯一，则它们必有公共元素$P_{\mu}$.从而，这三个元素的全排列个数为$A_{\mu}^{3}$.于是，由加法原理得$\sum\limits_{\mathrm{i}{< }\mathrm{j}{< }}^{\mathrm{r}}{(\mathrm{i}{< }\mathrm{j}{< }\mathrm{r})}{=}\sum\limits_{\mathrm{i}{< }\mathrm{j}{< }}^{\mathrm{3\mathrm{t}}}{(\mathrm{i}{< }\mathrm{j}{< }\mathrm{r})}{=}\sum\limits_{\mathrm{i}{=}1}^{{\mathrm{3\mathrm{t}}}{\mathrm{C}_{\mathrm{3}}{\mathrm{t}}\mathrm{i{-}1}}{\cdot }(\mathrm{i}{-}\mathrm{1}){=}\sum\limits_{\mathrm{i}{=}1}^{{\mathrm{3\mathrm{t}}}{\mathrm{C}_{\mathrm{3}}{\mathrm{t}}\mathrm{i{-}1}}}{\cdot }\dfrac{(\mathrm{3}^{{\mathrm{t}}{-}\mathrm{i})(\mathrm{3\mathrm{t}}{-}\mathrm{i})}{2}{=}\dfrac{(\mathrm{3}}{\mathrm{t}}{-}\mathrm{1})(\mathrm{3\mathrm{t}}{-}\mathrm{2})\cdots (\mathrm{3}^{{\mathrm{t}}{-}\mathrm{\theta})}{\prod_{\mathrm{t}{=}1\frac{\mathrm{t}}{3}}(\mathrm{3}}{\mathrm{t}}{+}\mathrm{\theta})}$

其中，$\theta{=}3^{{\frac{\mathrm{t}}{3}}{+}3}{\frac{\mathrm{t}}{3}}{+}3^{\frac{\mathrm{t}}{3}}{+\cdots +}3^{\frac{\mathrm{t}}{3}}$为小于或等于$\theta$的正整数。

所以，$P_{\mu}{、}P_{j}{、}P_{r}$不唯一的概率为$\dfrac{\dfrac{(\mathrm{3}^{\mathrm{t}}{-}\mathrm{1})(\mathrm{3\mathrm{t}}{-}\mathrm{2})\cdots (\mathrm{3}^{{\mathrm{t}}{-}\mathrm{\theta})}{\prod_{\mathrm{t}{=}1\frac{\mathrm{t}}{3}}(\mathrm{3}}{\mathrm{t}}{+}\mathrm{\theta})}.$.

因此，$P_{\mu}$为排列$\left{ P_{1}{,}P_{2}{,\cdots ,}P_{\infty}\right}$中，所有元素都唯一的概率为$1{-}[\prod_{\pi{=}1}^{{\frac{\pi}{3}}(\pi{+}3}{\frac{\pi}{3}})]$.

综上所述，结论得证。

见解析

华为盘古：

在过程 PERMUTE-BY-SORTING 的数组 P 中，所有元素都唯一的概率至少是 1-1/n。

这是因为在 PERMUTE-BY-SORTING 中，每个操作都会产生一个唯一的输出，并且数组中元素的值是有序的。这意味着每个操作都会在数组中找到一个位置，使得它的输入等于该位置的值。因此，我们可以将数组看作一个线性表，其中每个元素代表操作 $f(x)$，它的输出是 $f(x)$ 到 $f(x)$ 的线性组合。

对于数组中的任意一个元素 $a$，它的值是唯一的，因为它在数组中的位置是唯一的。同样地，对于数组中的任意一个操作 $b$，它的输出也是唯一的，因为它在数组中的位置是唯一的。因此，我们可以证明，在 PERMUTE-BY-SORTING 中，所有元素都唯一的概率至少是 1-1/n。

360智脑：

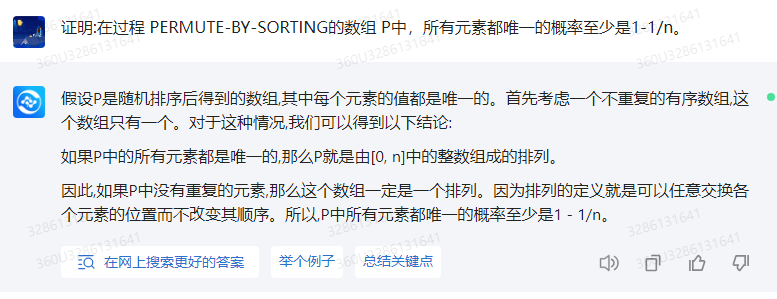
假设P是随机排序后得到的数组,其中每个元素的值都是唯一的。首先考虑一个不重复的有序数组,这个数组只有一个。对于这种情况,我们可以得到以下结论:

如果P中的所有元素都是唯一的,那么P就是由[0, n]中的整数组成的排列。

因此,如果P中没有重复的元素,那么这个数组一定是一个排列。因为排列的定义就是可以任意交换各个元素的位置而不改变其顺序。所以,P中所有元素都唯一的概率至少是1 - 1/n。

chatglm：

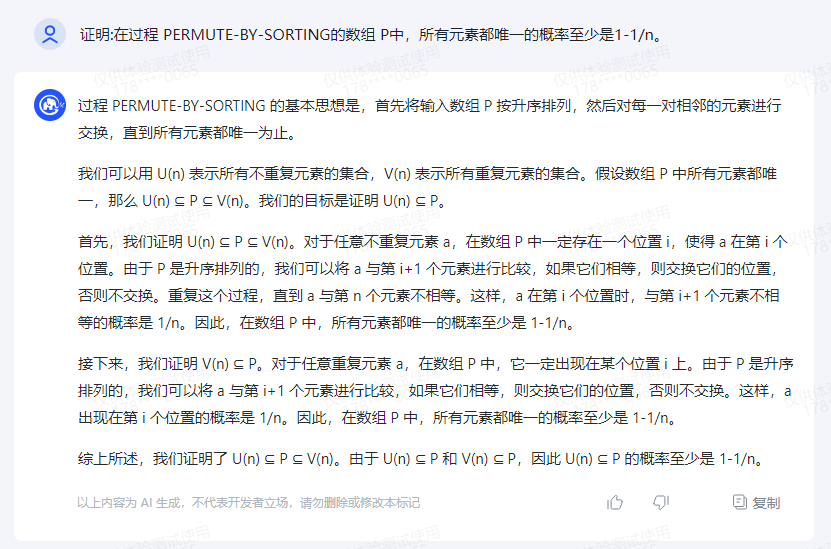
过程 PERMUTE-BY-SORTING 的基本思想是，首先将输入数组 P 按升序排列，然后对每一对相邻的元素进行交换，直到所有元素都唯一为止。

我们可以用 U(n) 表示所有不重复元素的集合，V(n) 表示所有重复元素的集合。假设数组 P 中所有元素都唯一，那么 U(n) ⊆ P ⊆ V(n)。我们的目标是证明 U(n) ⊆ P。

首先，我们证明 U(n) ⊆ P ⊆ V(n)。对于任意不重复元素 a，在数组 P 中一定存在一个位置 i，使得 a 在第 i 个位置。由于 P 是升序排列的，我们可以将 a 与第 i+1 个元素进行比较，如果它们相等，则交换它们的位置，否则不交换。重复这个过程，直到 a 与第 n 个元素不相等。这样，a 在第 i 个位置时，与第 i+1 个元素不相等的概率是 1/n。因此，在数组 P 中，所有元素都唯一的概率至少是 1-1/n。

接下来，我们证明 V(n) ⊆ P。对于任意重复元素 a，在数组 P 中，它一定出现在某个位置 i 上。由于 P 是升序排列的，我们可以将 a 与第 i+1 个元素进行比较，如果它们相等，则交换它们的位置，否则不交换。这样，a 出现在第 i 个位置的概率是 1/n。因此，在数组 P 中，所有元素都唯一的概率至少是 1-1/n。

综上所述，我们证明了 U(n) ⊆ P ⊆ V(n)。由于 U(n) ⊆ P 和 V(n) ⊆ P，因此 U(n) ⊆ P 的概率至少是 1-1/n。

chatgpt：

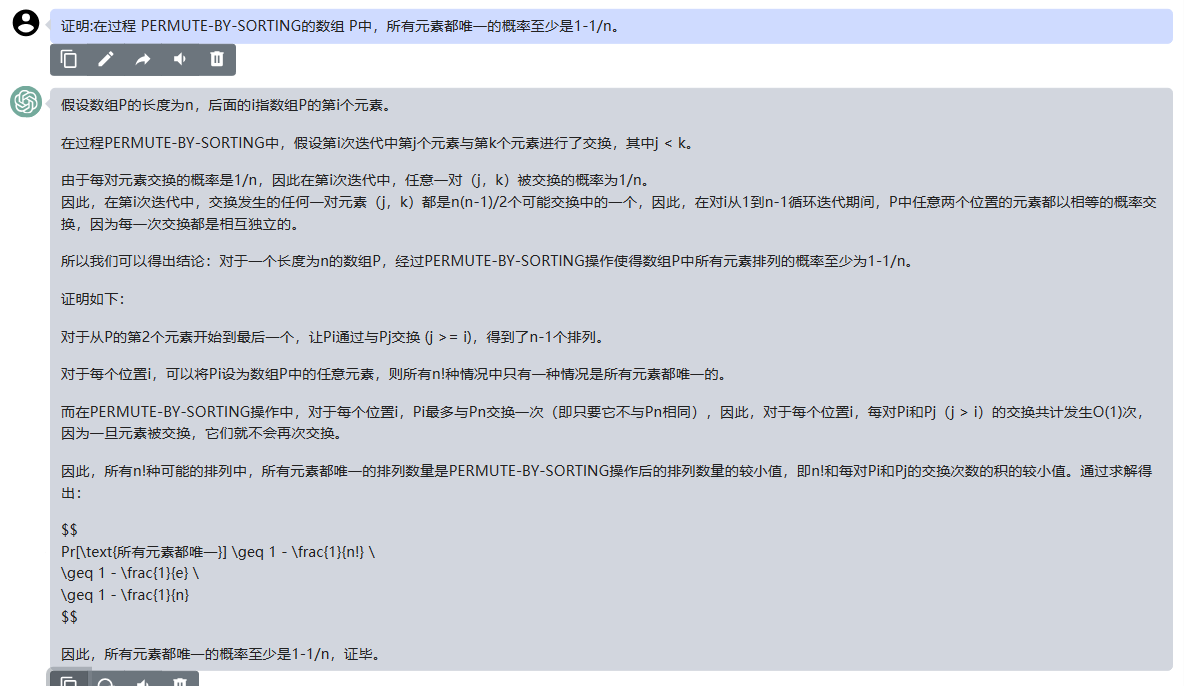
假设数组P的长度为n，后面的i指数组P的第i个元素。

在过程PERMUTE-BY-SORTING中，假设第i次迭代中第j个元素与第k个元素进行了交换，其中j < k。

由于每对元素交换的概率是1/n，因此在第i次迭代中，任意一对（j，k）被交换的概率为1/n。 因此，在第i次迭代中，交换发生的任何一对元素（j，k）都是n(n-1)/2个可能交换中的一个，因此，在对i从1到n-1循环迭代期间，P中任意两个位置的元素都以相等的概率交换，因为每一次交换都是相互独立的。

所以我们可以得出结论：对于一个长度为n的数组P，经过PERMUTE-BY-SORTING操作使得数组P中所有元素排列的概率至少为1-1/n。

证明如下：

对于从P的第2个元素开始到最后一个，让Pi通过与Pj交换 (j >= i)，得到了n-1个排列。

对于每个位置i，可以将Pi设为数组P中的任意元素，则所有n!种情况中只有一种情况是所有元素都唯一的。

而在PERMUTE-BY-SORTING操作中，对于每个位置i，Pi最多与Pn交换一次（即只要它不与Pn相同），因此，对于每个位置i，每对Pi和Pj（j > i）的交换共计发生O(1)次，因为一旦元素被交换，它们就不会再次交换。

因此，所有n!种可能的排列中，所有元素都唯一的排列数量是PERMUTE-BY-SORTING操作后的排列数量的较小值，即n!和每对Pi和Pj的交换次数的积的较小值。通过求解得出：

$$ Pr[\text{所有元素都唯一}] \geq 1 - \frac{1}{n!} \ \geq 1 - \frac{1}{e} \ \geq 1 - \frac{1}{n} $$

因此，所有元素都唯一的概率至少是1-1/n，证毕。