梯度更新:随机梯度,minbath梯度,全量梯度
动量法:引入一阶动量,动量法是为了解决传统的梯度下降算法收敛很慢的问题。相当于每次在进行参数更新的时候,都会将之前的速度考虑进来,加权梯度
AdaGrad:随机梯度优化算法依赖学习率参数,所以为了解决传统梯度的梯度下降算法对参数敏感的问题,因此我们需要自适应学习率
Adagrad优化算法就是在每次使用一个 batch size 的数据进行参数更新的时候,算法计算所有参数的梯度。对于每个参数,初始化一个变量 s 为 0,然后每次将该参数的梯度平方(这里出现了二阶!)求和累加到这个变量 s 上,然后在更新这个参数的时候,学习率 就变为:
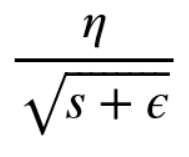
我们使用自适应的学习率就可以帮助算法在梯度大的参数方向减缓学习速率,而在梯度小的参数方向加快学习速率,这就可以促使神经网络的训练速度的加快。 Adagrad 的核心想法就是,如果一个参数的梯度一直都非常大,那么其对应的学习率就变小一点,防止震荡,而一个参数的梯度一直都非常小,那么这个参数的学习率就变大一点,使得其能够更快地更新,这就是Adagrad算法加快深层神经网络的训练速度的核心。
AdaDelta / RMSProp(引入二阶动量,使用二阶动量的滑动平均)
Adagrad存在的问题:因为是单调递增的,会使得学习率单调递减至0,可能会使得训练过程提前结束,即便后续还有数据也无法学到必要的知识。
Adam(引入一阶、二阶动量,使用二阶动量的滑动平均)
简单来说,Adam = Momentum + Adaptive Learning Rate。
标签:二阶,梯度,学习,算法,参数,动量,优化 From: https://www.cnblogs.com/qiaoqifa/p/17212759.html