双指针
类型:
- 2个指针指向不同的序列,比如归并排序
- 2个指针指向同一个序列,用的比较多,比如快速排序

通用模板
俗称的枚举右端点,遍历左端点
for (int i = 0, j = 0; i < n; i++) {
while (j < i && check(i,j)) j++;
// 每道题的具体逻辑
}
核心思想
对于形如
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
}
}
这一类的双层暴力循环,可能可以使用双指针来进行优化,从而能够把时间复杂度从O(n^2)降低到O(n)
位运算
-
获取一个数二进制的第k位:
x >> k & 1即,先将x右移k位,然后和1做与运算 -
获取一个数的二进制的最后一位1:
lowbit(x) = x & -x例如 x = 1010 lowbit(x) = 10, x = 101000 lowbit(x) = 1000
lowbit运算的原理是,
x & -x,由于-x采用补码表示,它等于对x的原码取反再加1,即-x = ~x + 1比如 x 的二进制表示是:100101000,对x取反得
011010111,加1得
011011000所以
x & (~x + 1),则x的最后一位1,被保留了下来,这个位置后面,两个数全是0,这个位置前面,两个数是取反,做与运算后也全为0。lowbit的最简单的应用:统计x的二进制表示中,1的个数。具体的实现方式是:每次对x做lowbit运算,并将运算结果从x中减去。循环做下去,直到x被减为0,一共减了多少次,x中就有多少个1。
离散化
有的数组,其元素的值域很大,比如数组中的元素取值都是[0, 10^9],但元素的个数很少,比如只有1000个元素。
有时(例如计数排序的思想),我们需要将元素的值,作为数组的下标来操作。此时不可能开一个10^9大小的数组。此时我们把这些元素,映射为从0(或者从1)开始的自然数。(也可以理解为对稀疏数组进行压缩)
例子如下:
有一个数组a,[1, 3, 100, 2000, 500000](已经排好序),我们把这个数组中的元素,映射为[0, 1, 2, 3, 4],这个映射的过程,称之为离散化
离散化有2个要点:
- 原数组a中若有重复元素,可能需要去重
- 如何根据a[i],算出其离散化后的值:由于原数组已经排好序,故这里用二分查找即可
代码模板
vector<int> v; // 待离散化的数组
sort(v.begin(), v.end()); // 将数组先排序
v.erase(unique(v.begin(), v.end()), v.end()); // 对数组进行去重
// 进行离散化, 将数组的值依次映射到 0,1,2,3,4,5, ... 等自然数
// 根据数的值, 求出其离散化的值
int find(int x) {
int l = 0, r = v.size() - 1;
while(l < r) { // 找到第一个大于等于x的离散化的值
int mid = l + r >> 1;
if(v[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1; // 是否加1, 跟题目相关, 若是前缀和差分等需要下标从1开始, 则需要加1
}
区间合并
给定很多个区间,若2个区间有交集,将二者合并成一个区间
做法思路:
- 先按照区间的左端点进行排序
- 然后遍历每个区间,进行合并即可维护一段区间,对于区间 i,可能有下面几种关系:
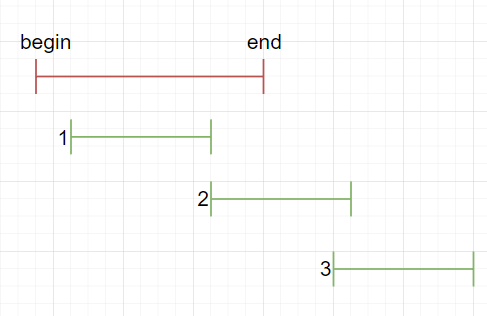
- 对于第一种情况,区间不变
- 对于第二种情况,end要变成区间i的右端点前面两种情况,可以合并为将end更新为end和区间i的右端点中的较大者
- 对于第三种情况,将当前维护的区间加入答案,并将维护的区间更新为区间i