第一章 基础算法一
快速排序
quick_sort(int q[], int l, int r)
q是待排序数组,l是待排序区间的左边界,r是右边界
- 确定分界点
x,可以取左边界的值q[l],或右边界的值q[r],或者中间位置的值q[(l + r)>>1] - 根据基准值,调整区间,使得左半边区间的值全都
≤ x,右半边区间的值全都≥ x
采用双指针,左指针i从左边界l-1开始,往右扫描,右指针j从右边界r+1开始,往左扫描
当满足条件q[i] < x时,i右移;直到不满足条件时,i停下;开始移动j
当满足条件q[i] > x时,j左移;直到不满足条件时,j停下;交换q[i]和q[j]
将i右移一位,j左移一位,重复上面的操作,直到i和j相遇。
此时左半区间的数都满足≤x,且左半区间的最后一个数的下标为j,右半区间的数都满足≥ x,且右半区间的第一个数的下标为i - 递归处理左右两段,递归操作
[l, j],[j + 1, r]区间,或者[l, i - 1],[i,r]区间即可
代码模板
void quick_sort(int q[], int l, int r) {
if(l >= r) return;
int x = q[(l + r) >> 1], i = l - 1, j = r + 1;
while (i < j) {
do i++; while (q[i] < x);
do j--; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j);
quick_sort(q, j + 1, r);
}
注意要点
当区间划分结束后,左指针i和右指针j的相对位置,只有2种情况
i = j + 1 i = j(此时i和j指向的元素,恰好等于基准值x)
若用j来作为区间的分界,则[l, j] 都是≤x,[j + 1, r]都是≥x
若用i来作为区间的分界,则[l, i - 1]都是≤x,[i, r]都是≥x
当取i作为分界的话,基准值x不能取到左边界q[l],否则会出现死循环,比如用例[1,2]。此时基准值可以取q[r],或者q[l + r + 1 >> 1],注意取中间位置的数时,要加个1,避免l + r >> 1的结果为l
当取j作为分界的话,基准值x不能取到右边界q[r],否则会出现死循环。此时基准值可以取q[l],或者q[l + r >> 1]
归并排序
- 确定分界点(一般是最中间)
mid = (l + r) >> 1, - 对左右两个区间递归排序
- 将左右两个有序数组归并,合二为一(使用双指针)
时间复杂度O(nlogn)
代码模板
int binary_search_1(int l, int r) {
while(l < r) {
int mid = l + r + 1 >> 1;
// 当下面是 l = mid 这样来更新的话,这里计算mid时要多加1,否则会出现边界问题
if(check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
二分查找
整数二分
二分的本质不是单调性,有单调性一定可以二分,可以二分不一定有单调性
二分的本质是边界,假设给定一个区间,如果能够根据某个条件,将区间划分为左右两部分,使得左半边满足这个条件,右半边不满足这个条件(或者反之)。就可以用二分来查找左右两部分的边界点。
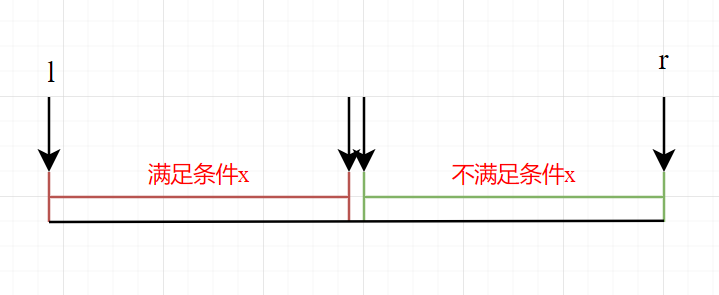
寻找红色二分点
- 取
mid = l + r + 1 >> 1 - 判断
mid是否满足条件,check(mid) - 如果
mid满足条件,那么答案(红色边界点)一定在[mid,r]之间,此时更新l = mid - 如果
mid不满足条件,那么答案(红色边界点)一定在[l,mid-1]之间,此时更新r = mid - 1
注意,当采用l = mid和r = mid - 1这种更新方式时,计算mid时,要加上1(向上取整),即mid = l + r + 1 >> 1。否则,在l = r - 1时,计算mid时若不加1,则mid = l + r >> 1 = l,这样更新l = mid,就是l = l,会导致死循环。所以要向上取整,采用mid = l + r + 1 >> 1。
模板
int binary_search_1(int l, int r) {
while(l < r) {
int mid = l + r + 1 >> 1;
// 当下面是 l = mid 这样来更新的话,这里计算mid时要多加1,否则会出现边界问题
if(check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
寻找绿色二分点
- 取
mid = l + r >> 1 - 判断
mid是否满足条件,check(mid) - 如果
mid满足条件,那么答案(绿色边界点)一定在[l,mid]之间,此时更新r = mid - 如果
mid不满足条件,那么答案(绿色边界点)一定在[mid + 1,r]之间,此时更新l = mid + 1
同理,当采用r = mid和 l = mid + 1这种更新方式时,计算mid时不能加1,在l = r - 1时,若计算mid时加1,则mid = l + r + 1 >> 1 = r,这样更新r = mid。就是r = r,会导致死循环。
模板
int binary_search_2(int l, int r) {
while(l < r) {
int mid = l + r >> 1;
if(check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
浮点数二分
相比整数二分,浮点数二分无需考虑边界问题,比较简单。
当二分的区间足够小时,可以认为已经找到了答案,如当r - l < 1e-6 ,停止二分。
或者直接迭代一定的次数,比如循环100次后停止二分。
数的三次方根
给定一个浮点数 n,求它的三次方根。
输入格式
共一行,包含一个浮点数 n。
输出格式
共一行,包含一个浮点数,表示问题的解。
注意,结果保留 6 位小数。
数据范围
−10000≤n≤10000
输入样例:
1000.00
输出样例:
10.000000
#include <iostream>
using namespace std;
const double esp = 1e-8;
int main() {
double n;
cin >> n;
double l = -1000, r = 1000;
while (r - l > esp) {
double mid = (l + r) / 2.0;
if (mid * mid * mid >= n) r = mid;
else l = mid;
}
printf("%f", l);
return 0;
}