高精度
A + B:两个大整数相加
A - B:两个大整数相减
A × b:一个大整数乘一个小整数
A ÷ b:一个大整数除以一个小整数
大整数的存储:用一个数组来存大整数的每一位上的数。
这里将大整数的个位,存到数组的第一位,大整数的最高位,存到数组的最后一位,即采用小端序
高精度加法
高精度加法的流程,就是模拟人手动做加法的过程,将每一位依次相加,并带上前一位的进位。
代码流程
// C++
vector<int> add(vector<int> &A, vector<int> &B) {
int t = 0; // 进位
vector<int> C;
for(int i = 0; i < A.size() || i < B.size(); i++) {
if(i < A.size()) t += A[i];
if(i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
// 若最高位有进位
if(t) C.push_back(t);
return C;
}
int main() {
string a, b;
cin >> a >> b;
vector<int> A, B;
for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
for(int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
vector<int> C = add(A, B);
for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
}
高精度减法
先判断一下A和B的相对大小,若
A >= B,则直接计算减法
A < B,计算B - A,并在结果前面加上负号-
高精度减法的流程,也是模拟人手动做减法的流程,当某一位不够减时,会有借位的概念
代码流程
// C++
// 判断是否有 A >= B
bool cmp (vector<int>& A, vector<int>& B) {
if (A.size() != B.size()) return A.size() > B.size();
for (int i = A.size() - 1; i >= 0; i++) {
if(A[i] != B[i]) return A[i] > B[i];
}
return true;
}
// 一定要保证 A >= B
vector<int> sub (vector<int> &A, vector<int> &B) {
vector<int> C;
int t = 0; // 借位
for (int i = 0; i < A.size(); i++) {
t = A[i] - t;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if (t < 0) t = 1; // 向上一位借位
else t = 0;
}
while (C.size() > 1 && C.back() == 0) C.pop_back(); // 去掉前导零
return C;
}
int main() {
string a, b;
cin >> a >> b;
vector<int> A, B;
for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
for(int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
if (cmp(A, B)) {
auto C = sub(A, B);
for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
} else {
auto C = sub(B, A);
printf("-");
for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
}
}
高精度乘法
A × b
把b看成一个整体,和A的每一位去做乘法。例如:123 × 12。
首先从A的最低位开始,计算3 × 12,得36,则结果中的个位为:36 % 10 = 6,产生的进位为36 / 10 = 3;继续下一位,计算2 × 12,得24,加上进位3,得27,结果中的十位为:27 % 10 = 7,产生的进位是27 / 10 = 2;继续下一位,1 × 12 + 2 = 14,则百位上的结果为14 % 10 = 4,产生进位14 / 10 = 1,则最终结果为1476。
代码流程
// C++
vector<int> mul(vector<int> &A, int b)
{
vector<int> C;
int t = 0;
for (int i = 0; i < A.size() || t; i ++ )
{
if (i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main() {
string a;
int b;
cin >> a >> b;
vector<int> A;
for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
vector<int> C = mul(A, b);
for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
}
高精度除法
算法的流程,是模拟人手动做除法的流程。从最高位除起,依次做商和取余。每一轮的余数,乘以10,加上下一位的数,作为下一轮的被除数。
代码流程
// C++
// r 用引用传递
vector<int> div(vector<int> &A, int b, int &r)
{
vector<int> C;
// 从最高位开始计算
for (int i = A.size(); i >= 0; i--) {
r = r * 10 + A[i]; // 本轮的被除数
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main() {
string a;
int b;
cin >> a >> b;
vector<int> A;
for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
int r = 0;
vector<int> C = div(A, b, r);
for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
printf("\n%d\n", r);
}
前缀和
一维前缀和
假设有一个数组:\(a_{1},a_{2},a_{3},a_{4},a_{5},…,a_{n}\)(注意,下标从1开始)
前缀和 \(S_{i} = a_{1} + a_{2} + a_{3} + … + a_{i}\)(即前i个数的和)
前缀和计算:前缀和满足 \(S_{i} = S_{i-1} + a_{i}\)},定义\(S_{0} = 0\)
前缀和作用:求任意一段区间的所有数的和。比如,要求区间[l, r]的全部元素的和,我们可以用 \(S_{r} - S_{l-1}\)来计算,如果没有前缀和数组,就需要遍历数组,时间复杂度O(n)
代码模板
// S[i] = a[1] + a[2] + ... a[i]
// 构造前缀和数组:
for (int i = 1; i <= n; i++) S[i] = S[i - 1] + a[i];
// 计算[l, r]的和
a[l] + ... + a[r] = S[r] - S[l - 1]
二维前缀和
假设有如下的矩阵
\(a_{11},a_{12},a_{13},a_{14},…,a_{1n}\)
\(a_{21},a_{22},a_{23},a_{24},…, a_{2n}\)
…
…
\(a_{m1},a_{m2},a_{m3},a_{m4},…,a_{mn}\)前缀和 \(S_{ij}\)表示点 \(a_{ij}\) 及其左上角区域的所有数的和。
经过简单推导(面积计算),可以得到 \(S_{ij} = S_{i-1,j} + S_{i,j-1} + a_{ij} - S_{i-1,j-1}\)
若要计算左上角边界点为\([x_{1}, y_{1}]\),右下角点为\([x_{2}, y_{2}]\),这2个点之间部分的子矩阵的和(也是求任意一段区间内所有数的和),经过简单推导,能够得到下面的公式:
\(S = S_{x_{2},y_{2}} - S_{x_{1}-1,y_{2}} - S_{x_{2},y_{1}-1} + S_{x_{1}-1,y_{1}-1}\)(由于矩阵中是离散的点,所以计算时边界需要减掉1)
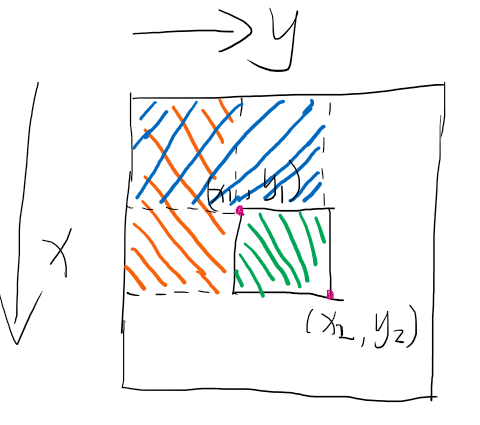
代码模板
S[i, j] = 第i行j列格子左上部分所有元素的和
// 构造前缀和矩阵
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
S[i][j] = S[i - 1][j] + S[i][j - 1] + a[i][j];
// 计算以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
差分
差分,是前缀和的逆运算
一维差分
假设有一个数组,\(a_{1},a_{2},a_{3},a_{4},a_{5},…,a_{n}\)
针对这个数组,构造出另一个数组,\(b_{1},b_{2},b_{3},b_{4},b_{5},…,b_{n}\)
使得a数组是b数组的前缀和,即使得 \(a_{i} = b_{1} + b_{2} + … + b_{i}\)
此时,称b数组为a数组的差分
数组b的构造\(b_{1} = a_{1},b_{2} = a_{2} - a_{1},b_{3} = a_{3} - a_{2},…,b_{n} = a_{n} - a_{n-1}\)
差分的作用:
若要对a数组中[l, r]区间内的全部元素都加上一个常数C,若直接操作a数组的话,时间复杂度是O(n)。而如果操作其差分数组b,则时间复杂度是O(1)。这是因为,数组a是数组b的前缀和数组,只要对 \(b_{l}\)这个元素加C,则a数组从l位置之后的全部数都会被加上C,但r位置之后的所有数也都加了C,所以我们通过对 \(b_{r+1}\) 这个数减去C,来保持a数组中r位置以后的数的值不变。
于是,对a数组的[l, r]区间内的所有数都加上一个常数C,就可以转变为对 \(b_{l}\) 加 C,对 \(b_{r+1}\)减 C。
因此在输入数组a时,可以先假想数组a和数组b的全部元素都是0。然后每次进行一次插入操作(指的是对数组a的[l, r]区间的每个数加上常数C),比如对a数组区间[1,1],加(插入)常数\(a_{1}\);对区间[2,2],加常数\(a_{2}\),…,这样在输入数组a的同时,就能够快速构造出其差分数组b。
代码模板
// 构造b数组
for (int i = 1; i <= n; i++)
b[i] += a[i], b[i + 1] -= a[i]
// 给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c
// 输出变化后的原数组
for (int i = 1; i <= n; i++)
cout << (b[i] += b[i - 1]) << " ";
二维差分
即差分矩阵
对于矩阵a,存在如下一个矩阵b
\(b_{11},b_{12},b_{13},b_{14},…,b_{1n}\)
\(b_{21},b_{22},b_{23},b_{24},…, b_{2n}\)
…
…
\(b_{m1},b_{m2},b_{m3},b_{m4},…,b_{mn}\)
使得\(a_{ij} =\) 矩阵b中[i, j]位置的左上角的所有数的和
称矩阵b为矩阵a的差分矩阵。
同样的,如果期望对矩阵a中左上角为\([x_{1}, y_{1}]\),右下角为\([x_{2}, y_{2}]\)的区域内的全部元素,都加一个常数C,则可以转化为对其差分矩阵b的操作。
先对b中\([x_{1}, y_{1}]\)位置上的元素加C,这样以来,a中\([x_{1}, y_{1}]\)这个点的右下角区域内的所有数都加上了C,但是这样就对\([x_{2}, y_{2}]\)之后的区域也都加了C。我们对[x2, y2]之外的区域需要保持值不变,所以需要进行减法。对\(b_{x_{2}+1,y_{1}}\) 减掉C,这样下图红色区域都被减了C,再对\(b_{x_{1},y_{2}+1}\)减掉C,这样下图蓝色区域都被减了C,而红色区域和蓝色区域有重叠,重叠的区域被减了2次C,所以要再加回一个C,即对\(b_{x_{2}+1,y_{2}+1}\)加上一个C。这样,就完成了对\([x_{1}, y_{1}]\),\([x_{2}, y_{2}]\)区域内的所有数(下图绿色区域),都加上常数C。
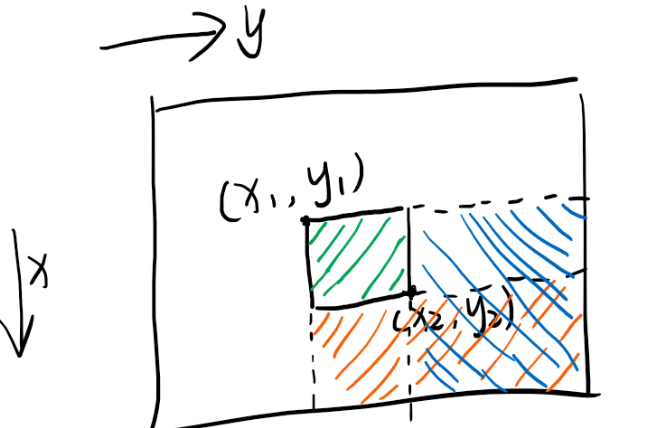
总结起来,对原矩阵a,在[x1, y1]到[x2, y2]区域内的全部元素加C,可以转换为对其差分矩阵b做如下操作
\(b_{x_{1},y_{1}}+C\) \(b_{x_1,y_{2}+1} - C\) \(b_{x_{2}+1,y} - C\) \(b_{x_{2}+1,y_{2}+1} + C\)
构造矩阵b,采用与上面相同的方式,先假设矩阵a和矩阵b的元素全都为0,此时矩阵b是矩阵a的差分矩阵,依次进行插入操作即可。
即对矩阵a的[1,1]到[1,1],加a[1][1],对[1,2]到[1,2],加a[1][2],…,如此即可构造出矩阵b
代码模板
// 构造差分矩阵可以看成对(i,j)到(i,j)插入a[i][j]
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
b[i][j] += a, b[i][j + 1] -= a, b[i + 1][j] -= a, b[i + 1][j + 1] += a;
// 给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c;
// 输出原数组
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++)
cout << (b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]) << " ";
cout << endl;
}