1. 单调栈简介
1.1 前言
今天是 2023/1/15,一中寒假集训阶段性的结束了。集训的学习笔记可以在本人 blogs 的【算法】标签栏中找。
马上就要过年了,提前祝大家新年快乐!
1.2 什么是单调栈
单调栈(monotone-stack)是一种基于栈进行的算法,且栈内元素(栈底到栈顶)都是(严格)单调递增或者单调递减的。
定义很抽象,不如拿一道题来直观的理解单调栈。
1.2.1 [luoguP5788]【模板】单调栈
给出项数为 \(n\) 的整数数列 \(a_{1 \dots n}\)。
定义函数 \(f(i)\) 代表数列中第 \(i\) 个元素之后第一个大于 \(a_i\) 的元素的下标,即 \(f(i)=\min_{i<j\leq n, a_j > a_i} \{j\}\)。若不存在,则 \(f(i)=0\)。
试求出 \(f(1\dots n)\)。
对于 \(100\%\) 的数据,\(1 \le n\leq 3\times 10^6\),\(1\leq a_i\leq 10^9\)。
1.2.2 Solve
建一个单调不减栈。
先来看一下单调栈的算法流程:
No.1

No.2
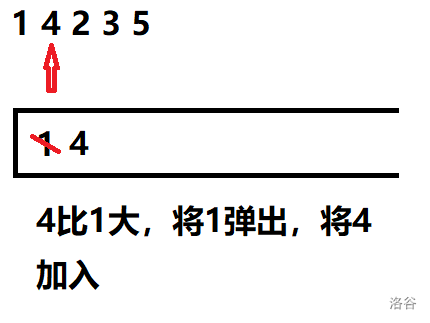
No.3
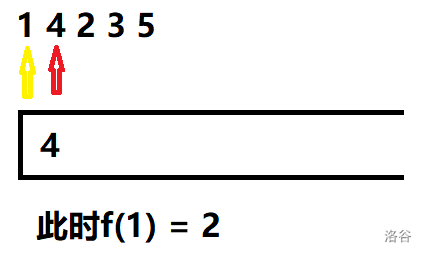
No.4
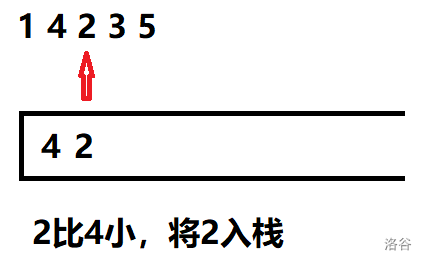
No.5
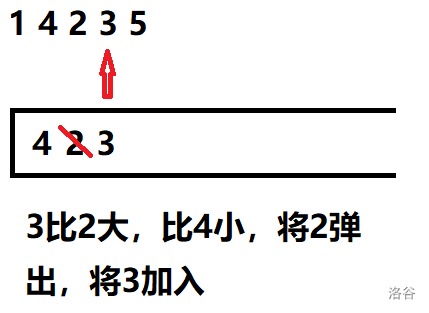
No.6
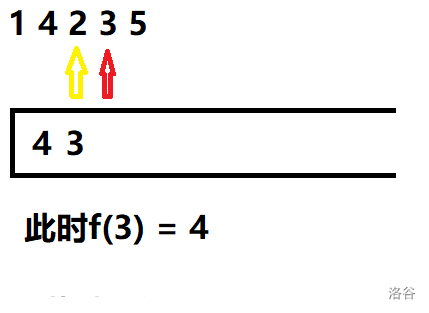
No.7
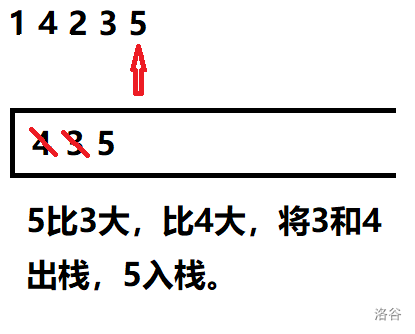
No.8
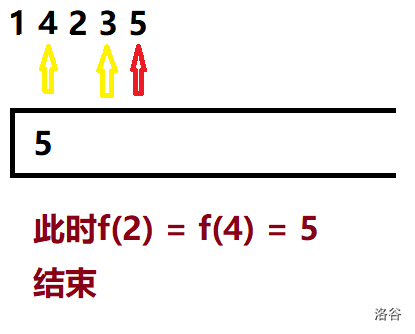
看完流程,是不是对单调栈的原理有了一定的认知了呢。
每一次加入新元素,都会从栈中弹出一些元素使得栈保持单调。通过观察发现,设栈中的一个元素在原序列中的编号为 \(x\),如果新加入的元素可以使得栈中元素弹出的话,那么新加入的元素则是我们要找的第一个大于 \(a_x\) 的元素。(仅限于单调不减栈)
所以每一次就在弹栈时更新答案即可。
怎么样?是不是豁然开朗。
1.3 Code & 单调栈的实现
以上一道题为例:
#include <bits/stdc++.h>
#define ll long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 3e6 + 10;
int n, a[N], f[N], stk[N], tot;
signed main(){
n = read();
For(i,1,n) {
a[i] = read();
while(tot && a[stk[tot]] < a[i]){//栈顶元素比新元素小,弹栈
f[stk[tot]] = i;
--tot;
}
stk[++tot] = i;//将新元素加入单调栈中
}
For(i,1,n) {
cout << f[i] << ' ';
}
return 0;
}
1.3 单调栈时间复杂度分析
有人会问了:上面的程序不是用了两个循环吗?两个循环不就是 \(O(n^2)\) 时间复杂度吗,那不还是超时了?
并非如此,我们发现,对于一个栈来说,在最坏的情况下,一个元素会进一次栈,出一次栈。\(n\) 个元素便最多会进出栈 \(2n\) 次。也就是说,尽管有两个循环,单调栈的时间复杂度依然是 \(O(n)\) 的!
因此我们可以看到,单调栈的时间复杂度是很优秀的。
2. 单调栈进阶
2.1 悬线法
我们来看一道经典的例题:
2.1.1 [luoguP1387] 最大正方形
在一个 \(n\times m\) 的只包含 \(0\) 和 \(1\) 的矩阵里找出一个不包含 \(0\) 的最大正方形,输出边长。\((1 \le n,m \le 100)\)
2.1.2 Solve
题意就是要找到一个最大全 \(1\) 正方形,并输出边长。
一眼暴力,枚举对顶点,\(O(1)\) 判断是否合法。很幸运,由于数据过水,您成功的过掉了此题。
这一题还有别的做法吗?,肯定有,它就是——悬线法+单调栈!
把样例搬过来:

由于它是一个矩阵,所以朴素版的单调栈已经对此“无能为力”。
既然单调栈不能变成二维,那么,我们就把矩阵转化成一维。即可用悬线法转化。
我们可以枚举每一行,然后用一个 \(h\) 数组记录一下此行到第 \(1\) 行连续的 \(1\)。长度。
然后用单调栈维护 \(h\) 数组中每一个数向左看和向右看第一个小于它的数的后一个数,最后把答案统计一下就行了。
算法流程如下:
No.1
统计第一层向上连续的 \(1\) 的长度,红色框住部分为连续的 \(1\)。
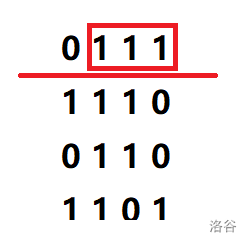
No.2
用单调栈维护 \(h\) 数组中每一个数向左看和向右看第一个小于它的数的后一个数(取范围最大的即可),如图中蓝色部分所示:
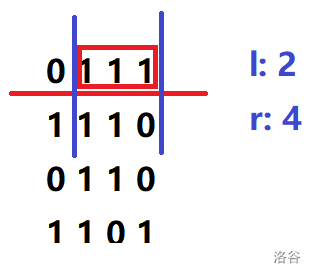
此时答案更新为 \(min(h_i,r-l+1)=min(1,2)=1\) (由于是正方形,所以答案应为长与宽中的最小值作为边长)。
No.3
第二行亦是如此,答案更新为 \(min(h_i,r-l+1)=min(2,2)=2\)。
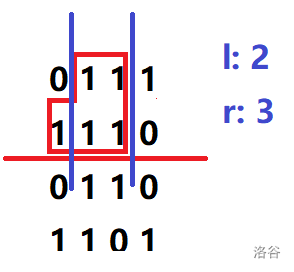
No.4
第三行,答案不做更新。
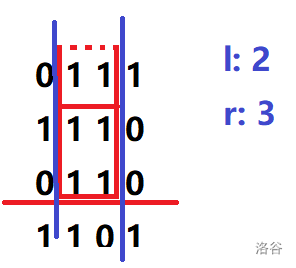
注:虚线部分表示实际答案统计的范围,已在上文中解释,不在此过多赘述。
No.5
第四行,答案不做更新。
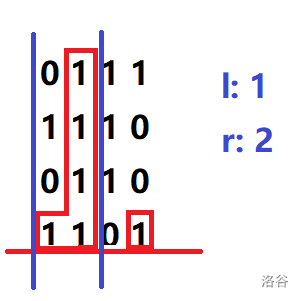
结束,答案为 \(2\)。
2.1.3 Code
#include <bits/stdc++.h>
#define ll long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 1e2 + 10;
int n, m, h[N], a[N][N], l[N], r[N], ans, top, stk[N];
void work1() {
top = 0;
FOR(i,m,1) {
while(top && h[stk[top]] > h[i]) {
l[stk[top]] = i + 1;
top--;
}
stk[++top] = i;
}
while(top) {
l[stk[top]] = 1;
top--;
}
}
void work2() {
top = 0;
For(i,1,m) {
while(top && h[stk[top]] > h[i]) {
r[stk[top]] = i - 1;
top--;
}
stk[++top] = i;
}
while(top) {
r[stk[top]] = m;
top--;
}
}
signed main() {
n = read(), m = read();
For(i,1,n) {
For(j,1,m) {
a[i][j] = read();
h[j] = (a[i][j] == 0 ? 0 : h[j] + 1);
}
work1();
work2();
For(j,1,m) {
ans = max(ans, min(h[j], r[j] - l[j] + 1));
}
}
cout << ans << '\n';
return 0;
}
3. 例题
3.1 P2659 美丽的序列
Problem
给定一个长度为 \(n\) 的序列 \(A\),求
\(1 \le n \le 10^6\)
Solve
枚举所有可能的区间最小值(即每一个数),再向外扩展区间。
我们发现最终答案肯定是按区间长度单调递增,所以我们要尽可能的把区间扩大。
扩大的极限就为每一个数左边第一个小于它的数的后一个数的位置与右边第一个小于它的数的前一个数的位置。
用单调栈解决即可。
Code
#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
void print(int x){
if(x<0){putchar('-');x=-x;}
if(x>9){print(x/10);putchar(x%10+'0');}
else putchar(x+'0');
return;
}
const int N = 2e6 + 10;
int n, a[N], ans, l[N], r[N], stk[N], top;
void work1() {
top = 0;
FOR(i,n,1) {
while(top && a[stk[top]] > a[i]) {
l[stk[top]] = i + 1;
top--;
}
stk[++top] = i;
}
while(top) {
l[stk[top]] = 1;
top--;
}
}
void work2() {
top = 0;
For(i,1,n) {
while(top && a[stk[top]] > a[i]) {
r[stk[top]] = i - 1;
top--;
}
stk[++top] = i;
}
while(top) {
r[stk[top]] = n;
top--;
}
}
signed main() {
n = read();
For(i,1,n) a[i] = read();
work1();
work2();
For(i,1,n) {
ans = max(ans, 1ll * a[i] * (r[i] - l[i] + 1));
}
cout << ans << '\n';
return 0;
}