今日任务
● 454.四数相加II
● 383. 赎金信
● 15. 三数之和
● 18. 四数之和
● 总结
详细布置
454.四数相加II
建议:本题是 使用map 巧妙解决的问题,好好体会一下 哈希法 如何提高程序执行效率,降低时间复杂度,当然使用哈希法 会提高空间复杂度,但一般来说我们都是舍空间 换时间, 工业开发也是这样。
题目链接/文章讲解/视频讲解:https://programmercarl.com/0454.%E5%9B%9B%E6%95%B0%E7%9B%B8%E5%8A%A0II.html
答案思路:
- 首先定义一个map,key放a和b两个数之和,value放a和b两个数之和出现的次数。
- 遍历大A和大B数字组,统计两个数字组元素之和,和出现的次数,放到地图中。
- 定义int变量count,用来统计a+b+c+d = 0出现的次数。
- 在遍历大C和大D数组,找到如果0-(c+d)在map中出现过的话,就用count把map中key对应的value也就是出现次数统计出来。
- 最后返回统计值count就可以了
class Solution {
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
Map<Integer, Integer> map = new HashMap<>();
int temp;
int res = 0;
//统计两个数组中的元素之和,同时统计出现的次数,放入map
for (int i : nums1) {
for (int j : nums2) {
temp = i + j;
if (map.containsKey(temp)) {
map.put(temp, map.get(temp) + 1);
} else {
map.put(temp, 1);
}
}
}
//统计剩余的两个元素的和,在map中找是否存在相加为0的情况,同时记录次数
for (int i : nums3) {
for (int j : nums4) {
temp = 0- (i + j);
if (map.containsKey(temp)) {
res += map.get(temp);
}
}
}
return res;
}
}
383. 赎金信
建议:本题 和 242.有效的字母异位词 是一个思路 ,算是拓展题
题目链接/文章讲解:https://programmercarl.com/0383.%E8%B5%8E%E9%87%91%E4%BF%A1.html
思路:创建长度26的数组,将magazine 包含的字符存入相应位置,遍历ransomNote,将相出现的应字符对应位置值--,
AC!!!
class Solution {
public boolean canConstruct(String ransomNote, String magazine) {
int[] record = new int[26];
char[] m = magazine.toCharArray();
char[] r = ransomNote.toCharArray();
for ( char i : m) {
record[i - 'a'] ++;
}
for ( char j : r) {
if (record[j - 'a'] != 0 ){
record[j - 'a']--;
}else{
return false;
}
}
for (int i : record) {
if (i < 0 ){
return false;
}
}
return true;
}
}
15. 三数之和
建议:本题虽然和 两数之和 很像,也能用哈希法,但用哈希法会很麻烦,双指针法才是正解,可以先看视频理解一下 双指针法的思路,文章中讲解的,没问题 哈希法很麻烦。
题目链接/文章讲解/视频讲解:https://programmercarl.com/0015.%E4%B8%89%E6%95%B0%E4%B9%8B%E5%92%8C.html
参考思路:
双指针:
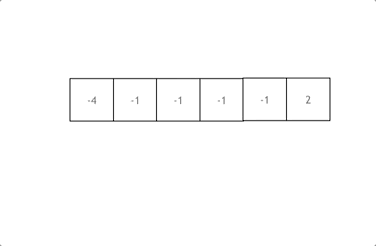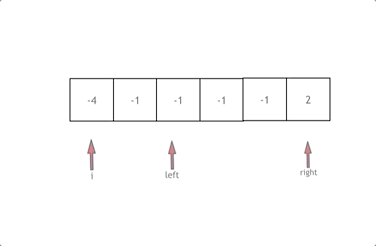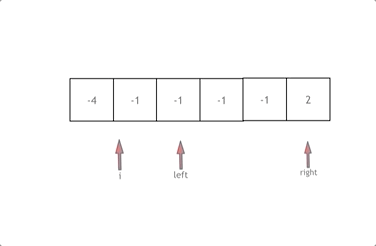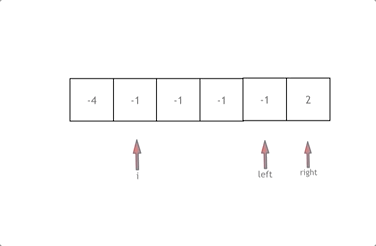
首先将数组排序,然后有一层for循环,i从下标0的地方开始,同时定一个下标left 定义在i+1的位置上,定义下标right 在数组结尾的位置上。
依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i],b = nums[left],c = nums[right]。
接下来如何移动left 和right呢, 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下标就应该向左移动,这样才能让三数之和小一些。
如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止。
时间复杂度:O(n^2)
去重逻辑的思考
#a的去重
说道去重,其实主要考虑三个数的去重。 a, b ,c, 对应的就是 nums[i],nums[left],nums[right]
a 如果重复了怎么办,a是nums里遍历的元素,那么应该直接跳过去。
但这里有一个问题,是判断 nums[i] 与 nums[i + 1]是否相同,还是判断 nums[i] 与 nums[i-1] 是否相同。
都是和 nums[i]进行比较,是比较它的前一个,还是比较他的后一个。
如果写法是这样:
if (nums[i] == nums[i + 1]) { // 去重操作
continue;
}
那就把三元组中出现重复元素的情况直接pass掉了。 例如{-1, -1 ,2} 这组数据,当遍历到第一个-1 的时候,判断 下一个也是-1,那这组数据就pass了。
要做的是 不能有重复的三元组,但三元组内的元素是可以重复的!
所以这里是有两个重复的维度。
那么应该这么写:
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
这么写就是当前使用 nums[i],我们判断前一位是不是一样的元素,在看 {-1, -1 ,2} 这组数据,当遍历到 第一个 -1 的时候,只要前一位没有-1,那么 {-1, -1 ,2} 这组数据一样可以收录到 结果集里。
这是一个非常细节的思考过程。
List<List<Integer>>:其是在List1<>中再放一个List2<>,List1中每个List2的长度可以是任意的,而不是像二维数组那样维度固定。
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
// 找出a + b + c = 0
// a = nums[i], b = nums[left], c = nums[right]
for (int i = 0; i < nums.length; i++) {
// 排序后如果第一个元素大于零,那么无论如何组合都不可能凑成三元组,直接返回
if (nums[i] > 0){
return res;
}
// 正确去重a
if (i > 0 && nums[i] == nums[i - 1]){
continue;
}
int l = i + 1;
int r = nums.length - 1;
while (l < r){
// 去重复逻辑如果放在这里,0,0,0 的情况,可能直接导致 right<=left 了,从而漏掉了 0,0,0 这种三元组
/*
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
*/
int sum = nums[i] + nums[l] + nums[r];
if (sum > 0){
r--;
}else if (sum < 0){
l++;
}else {
res.add(Arrays.asList(nums[i], nums[l], nums[r]));
// 去重逻辑应该放在找到一个三元组之后,对b 和 c去重
while(l < r && nums[r] == nums[r - 1]) r--;
while(l < r && nums[l] == nums[l + 1]) l++;
// 找到答案时,双指针同时收缩
r--;
l++;
}
}
}
return res;
}
}
List<String> list = Arrays.asList("a","b","c");
(1)该方法适用于对象型数据的数组(String、Integer...)
(2)该方法不建议使用于基本数据类型的数组(byte,short,int,long,float,double,boolean)
(3)该方法将数组与List列表链接起来:当更新其一个时,另一个自动更新
(4)不支持add()、remove()、clear()等方法
用此方法得到的List的长度是不可改变的,
当你向这个List添加或删除一个元素时(例如 list.add("d");)程序就会抛出异常
总结:如果你的List只是用来遍历,就用Arrays.asList()。
如果你的List还要添加或删除元素,还是乖乖地new一个java.util.ArrayList,然后一个一个的添加元素。
18. 四数之和
建议: 要比较一下,本题和 454.四数相加II 的区别,为什么 454.四数相加II 会简单很多,这个想明白了,对本题理解就深刻了。 本题 思路整体和 三数之和一样的,都是双指针,但写的时候 有很多小细节,需要注意,建议先看视频。
题目链接/文章讲解/视频讲解:https://programmercarl.com/0018.%E5%9B%9B%E6%95%B0%E4%B9%8B%E5%92%8C.html
思路:模拟类似三数之和写
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
if (nums.length <= 3){
return res;
}
for (int i = 0; i < nums.length; i++) {
int b = i + 1;
int c = i + 2;
int d = nums.length - 1;
while (c < d){
int sum = nums[i] + nums[b] + nums[c] + nums[d];
if (sum > target){
d--;
}else if (sum < target){
//出现问题,可能只需要移动c,不用移动b
b++;
c++;
}else {
res.add(Arrays.asList(nums[i], nums[b] , nums[c] , nums[d]));
while(c < d && nums[d] == nums[d - 1]) d--;
while(c < d && nums[c] == nums[c + 1]) c++;
d--;
b++;
c++;
}
}
}
return res;
}
}
参考答案:
四数之和,和15.三数之和(opens new window)是一个思路,都是使用双指针法, 基本解法就是在15.三数之和(opens new window)的基础上再套一层for循环。
但是有一些细节需要注意,例如: 不要判断nums[k] > target 就返回了,三数之和 可以通过 nums[i] > 0 就返回了,因为 0 已经是确定的数了,四数之和这道题目 target是任意值。比如:数组是[-4, -3, -2, -1],target是-10,不能因为-4 > -10而跳过。但是我们依旧可以去做剪枝,逻辑变成nums[i] > target && (nums[i] >=0 || target >= 0)就可以了。
15.三数之和(opens new window)的双指针解法是一层for循环num[i]为确定值,然后循环内有left和right下标作为双指针,找到nums[i] + nums[left] + nums[right] == 0。
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值,依然是循环内有left和right下标作为双指针,找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况,三数之和的时间复杂度是O(n^2),四数之和的时间复杂度是O(n^3) 。
那么一样的道理,五数之和、六数之和等等都采用这种解法。
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
for (int i = 0; i < nums.length; i++) {
if (nums[i] > 0 && nums[i] > target) {
return res;
}
if (i > 0 && nums[i - 1] == nums[i]) {
continue;
}
for (int j = i + 1; j < nums.length; j++) {
if (j > i + 1 && nums[j] == nums[j - 1]) {
continue;
}
int l = j + 1;
int r = nums.length - 1;
while (l < r){
long sum = (long)nums[i] + nums[j] + nums[l] + nums[r];
if (sum > target){
r--;
}else if (sum < target){
l++;
}else {
res.add(Arrays.asList(nums[i], nums[j], nums[l], nums[r]));
while(l < r && nums[r] == nums[r - 1]) r--;
while(l < r && nums[l] == nums[l + 1]) l++;
r--;
l++;
}
}
}
}
return res;
}
}
标签:四数,15,nums,int,三数,随想录,right,left From: https://www.cnblogs.com/gaoyuan2lty/p/16916983.html