Sadegh Aliakbarian-2021-ContextuallyPlausibleDiverse3DHumanMotionPrediction-ICCV

标签：Sadegh right VAE mu ICCV 2021 mathrm sigma left

# Contextually Plausible and Diverse 3D Human Motion Prediction #paper

---

1. paper-info

1.1 Metadata

• Author:: [[Sadegh Aliakbarian]], [[Fatemeh Saleh]], [[Lars Petersson]], [[Stephen Gould]], [[Mathieu Salzmann]]
• 作者机构::
• Keywords:: #HMP , #VAE
• Journal:: #ICCV
• Date:: [[2021]]
• 状态:: #Done
• 链接:: https://openaccess.thecvf.com/content/ICCV2021/html/Aliakbarian_Contextually_Plausible_and_Diverse_3D_Human_Motion_Prediction_ICCV_2021_paper.html
• 修改时间:: 2022.11.7

1.2. Abstract

We tackle the task of diverse 3D human motion prediction, that is, forecasting multiple plausible future 3D poses given a sequence of observed 3D poses. In this context, a popular approach consists of using a Conditional Variational Autoencoder (CVAE). However, existing approaches that do so either fail to capture the diversity in human motion, or generate diverse but semantically implausible continuations of the observed motion. In this paper, we address both of these problems by developing a new variational framework that accounts for both diversity and context of the generated future motion. To this end, and in contrast to existing approaches, we condition the sampling of the latent variable that acts as source of diversity on the representation of the past observation, thus encouraging it to carry relevant information. Our experiments demonstrate that our approach yields motions not only of higher quality while retaining diversity, but also that preserve the contextual information contained in the observed motion.

---

2. Introduction

• 领域：
  • diverse 3D human motion prediction
• VAE-based的方法：此类网络中的网络操作和训练数据都是确定的。
  • 无法生成多样性和具有上下文信息的动作序列的原因：
    1. 当信息量很大时，无法捕捉信息中的多样性
    2. CVAE的预测过程收到潜在变量的一般先验的阻碍，推理过程中，先验没有与潜在变量结合。（潜在变量与条件独立）
• 作者的方法：
  • 学习人体动作中的多模态，生成多样化且具有上下文和语义信息的动作序列。
• 方法对比：

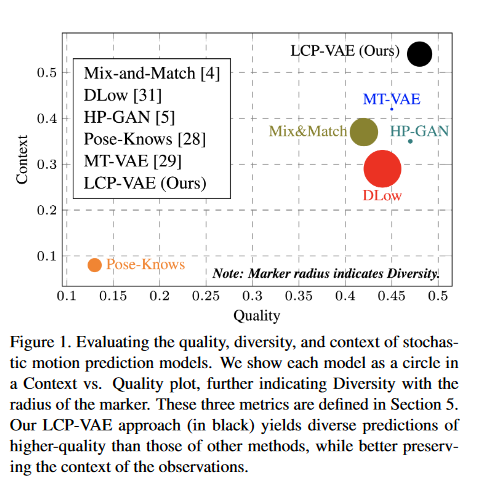
Fig.1. Quality
Source: https://openaccess.thecvf.com/content/ICCV2021/html/Aliakbarian_Contextually_Plausible_and_Diverse_3D_Human_Motion_Prediction_ICCV_2021_paper.html

3. Motivation

• VAE

\[\log p_{\theta}(x) \geq \mathbb{E}_{q_{\phi}(z \mid x)}\left[\log p_{\theta}(x \mid z)\right]-K L\left(q_{\phi}(z \mid x) \| p(z)\right) \]

• CVAE

\[\begin{aligned} \log p_{\theta}(x \mid c) & \geq \mathbb{E}_{q_{\phi}(z \mid x, c)}\left[\log p_{\theta}(x \mid z, c)\right] \\ &-K L\left(q_{\phi}(z \mid x, c) \| p(z \mid c)\right) \end{aligned} \]

在CVAE中\(z\)和\(c\)是独立的，于是作者在CVAE的基础上学习基于条件的潜在变量而不是单独学习潜在变量。
使用先验分布\(p(z|c)\),而不是使用\(p(z)\)

4. Approach: LCP-VAE

Fig2. LCP-VAE
Source:

模型由两个自编码器组成，一个用于编码观测序列，一个用于编码未来序列。

4.1. Stochastically Conditioning the Decoder

CS-VAE用于重构condition(i.e. the observed past motion)

改变之后，重参数技巧变为：

\[\begin{aligned} z=\mu+\sigma \odot z_{c} &=\mu+\sigma \odot\left(\mu_{c}+\sigma_{c} \odot \epsilon\right) \\ &=\underbrace{\left(\mu+\sigma \odot \mu_{c}\right)}_{\text {LCP-VAE's mean }}+\underbrace{\left(\sigma \odot \sigma_{c}\right)}_{\text {LCP-VAE's std. }} \odot \epsilon, \end{aligned} \]

4.2. Learning Detail

定义：
\(D=\{X_1,X_2,...,X_N\}\)：\(N\)个训练动作序列
\(X_i=\{x_i^1,...,x_i^T\}\)：数据库中第\(i\)个训练序列，由\(T\)个时间步的动作组成。
\(x_i^t = \{x_{i,1}^t,...,x_{i,J}^t\}\)：每个时间步的姿态表征。\(J\)表示关节数量
CS-VAE：损失函数形式，和标准VAE的损失函数一致

\[\begin{aligned} \mathcal{L}_{\text {prior }}^{\mathrm{CS}-\mathrm{VAE}} &=K L\left(\mathcal{N}\left(\mu_{c}, \operatorname{diag}\left(\sigma_{c}\right)^{2}\right) \| \mathcal{N}(0, I)\right) \\ &=-\frac{1}{2} \sum_{j=1}^{d}\left(1+\log \left(\sigma_{c_{j}}^{2}\right)-\mu_{c_{j}}^{2}-\sigma_{c_{j}}^{2}\right), \end{aligned} \]

LCP-VAE：损失函数

\[\begin{array}{l} \mathcal{L}_{\text {prior }}^{\mathrm{LCP}-\mathrm{VAE}}= \\ K L\left(\mathcal{N}\left(\mu+\sigma \odot \mu_{c}, \operatorname{diag}\left(\sigma \odot \sigma_{c}\right)^{2}\right) \| \mathcal{N}\left(\mu_{c}, \operatorname{diag}\left(\sigma_{c}\right)^{2}\right)\right) . \end{array} \]

\[ \begin{aligned} \mathcal{L}_{\text {prior }}^{\mathrm{LCP}-\mathrm{VAE}} &=-\frac{1}{2}\left[\log \frac{1}{|\Sigma|}-d+\operatorname{tr}\{\Sigma\}\right.\\ &\left.+\left(\mu_{c}-\left(\mu+\Sigma \mu_{c}\right)\right)^{T} \Sigma_{c}^{-1}\left(\mu_{c}-\left(\mu+\Sigma \mu_{c}\right)\right)\right] . \end{aligned}\]

同时加上重构误差：

\[\mathcal{L}_{r e c}=-\sum_{k=t^{\prime}}^{T^{\prime}} \sum_{j=1}^{J}\left\|\hat{x}_{i, j}^{k}-x_{i, j}^{k}\right\|^{2} \]

总的损失函数：

\[\mathcal{L}=\lambda\left(\mathcal{L}_{\text {prior }}^{\mathrm{CS}-\mathrm{VAE}}+\mathcal{L}_{\text {prior }}^{\mathrm{LCP}-\mathrm{VAE}}\right)+\mathcal{L}_{\text {rec }}^{\mathrm{CS}-\mathrm{VAE}}+\mathcal{L}_{\text {rec }}^{\mathrm{LCP}-\mathrm{VAE}} \]

在训练过程中，首先固定LCP-VAE的损失函数，更新CS-VAE;更新完成之后，固定CS-VAE的损失函数，更新LCP-VAE的损失函数。
\(\lambda\)：从0线性增长到1，这样在刚开始时能够强迫模型编码更多的多样化信息。

5. Experiments

• datasets
  • Human3.6M
  • CMU MoCap
  • Penn Action
• Evaluation Metrics
  • 重构损失：用KL散度来衡量
  • quality：训练一个二分类器
  • diversity metrics：average distance between all pairs of \(K\) motions
  • context metric

5.1. Comparison to the State of the Art

• baselines:
  1. Mix-and-Match[link]
  2. HP-GAN[link]
  3. Pose-Knowslink
  4. MT-VAElink
  5. DLownotelink

6. 总结：

该文章大致由两部分VAE构成，第一个VAE对条件进行编码，第二个VAE对未来序列进行编码，第二个VAE的潜在编码是在第一个VAE训练出的潜在变量的基础上进行重参数构造而来。用作者的话说就是传统的VAE的\(z\)和条件\(c\)是相互独立的，VAE只是使用先验\(p(z)\)，而本文使用\(p(z|c)\)。建立在这种模式之上，生成的动作序列可以是同类型的(生成 关于working 相关的动作，产生的多种动作序列都是在这个标签下。)

---

标签：Sadegh,right,VAE,mu,ICCV,2021,mathrm,sigma,left
From： https://www.cnblogs.com/guixu/p/16868692.html