Legacy
分析
模板题
利用线段树完成优化建图。
如果按照题目的要求去建边,我们直接的不论是时间还是空间都炸了,\(O(n^2)\)。
我们看到其中的第一二个操作都是从某个单点向区间连边。
这种区间操作,我们考虑一下,能否利用,每一个区间都可以表示为线段树上logn个区间来减少边的个数。
我们就拿2操作来举例。现在假设假如有一个点要与[l,3]的点连边权为w的边,那么我们建出线段树:
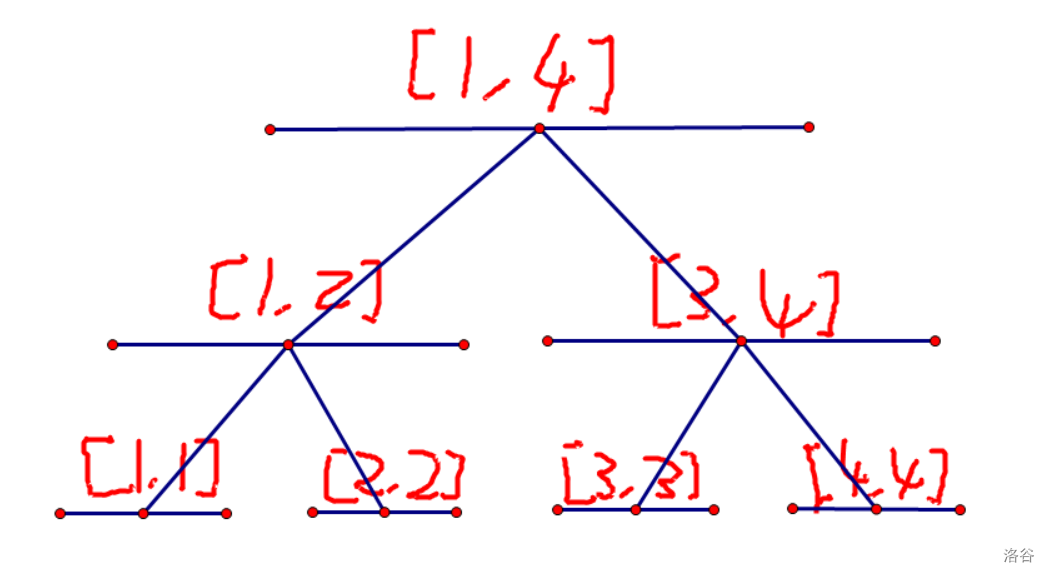
将[1,3]拆成[1,2]与[3,3]然后分别连边,边权为w(图中橙色的边):
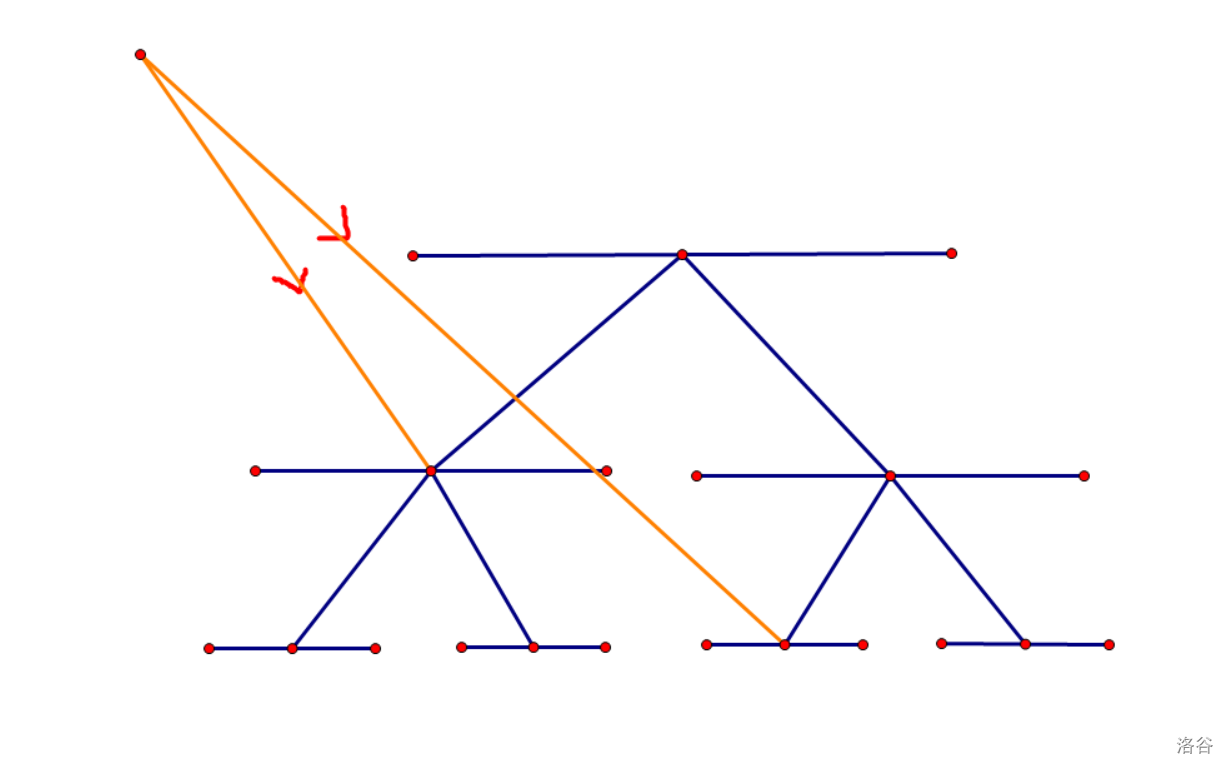
但是仅仅只连着两条边是肯定不够的,因为你只将这个点与一个区间表示的点连了边,并没有将其连到具体的单点上。
因此我们还从每个区间想起子区间连边,由于你向下走,从一个大区间对应到一个小区间没有代价,因此这些边的边权为0。
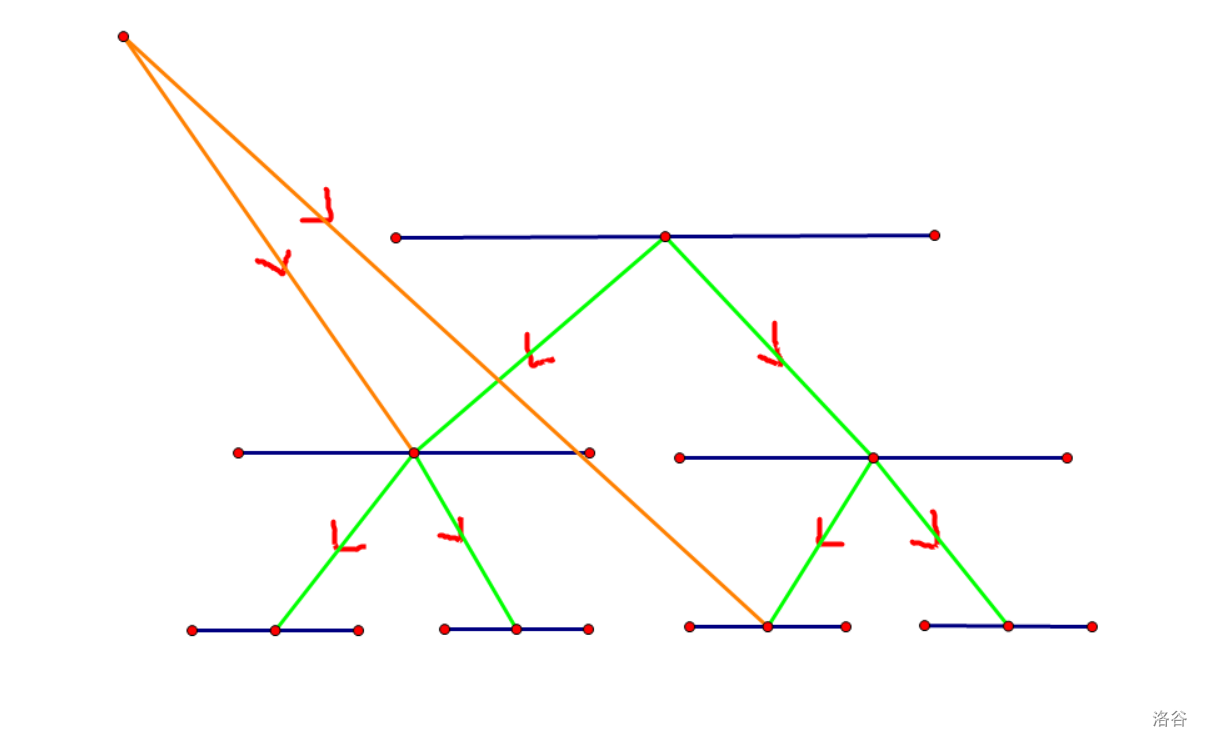
操作三也同理,只不过要将之前所有连的边都反向。
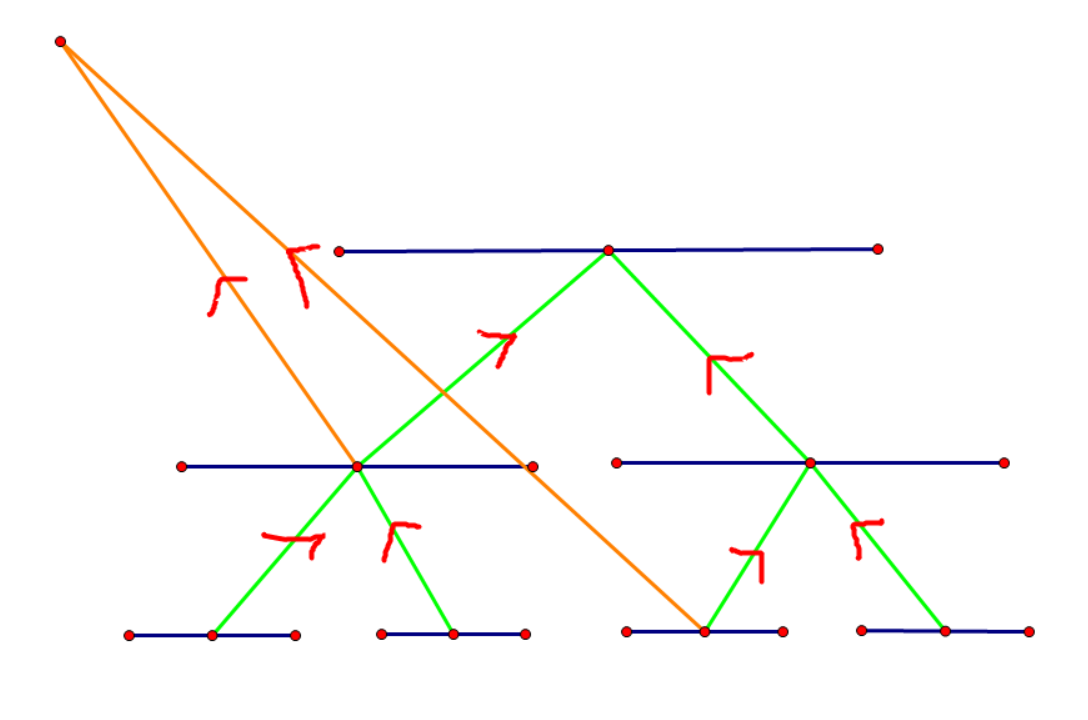
以上是操作2与操作3分开来考虑的情形,那么操作2与操作3相结合怎么办?
显然你不能把它们揉到一起去,因为你线段树上每条边向上向下边权都为0,故从源点到每个点的最短路也为0,这肯定是不太行。
因此我们建两颗线段树,第一棵树只连从上到下的边,第二课只连自下而上的边:
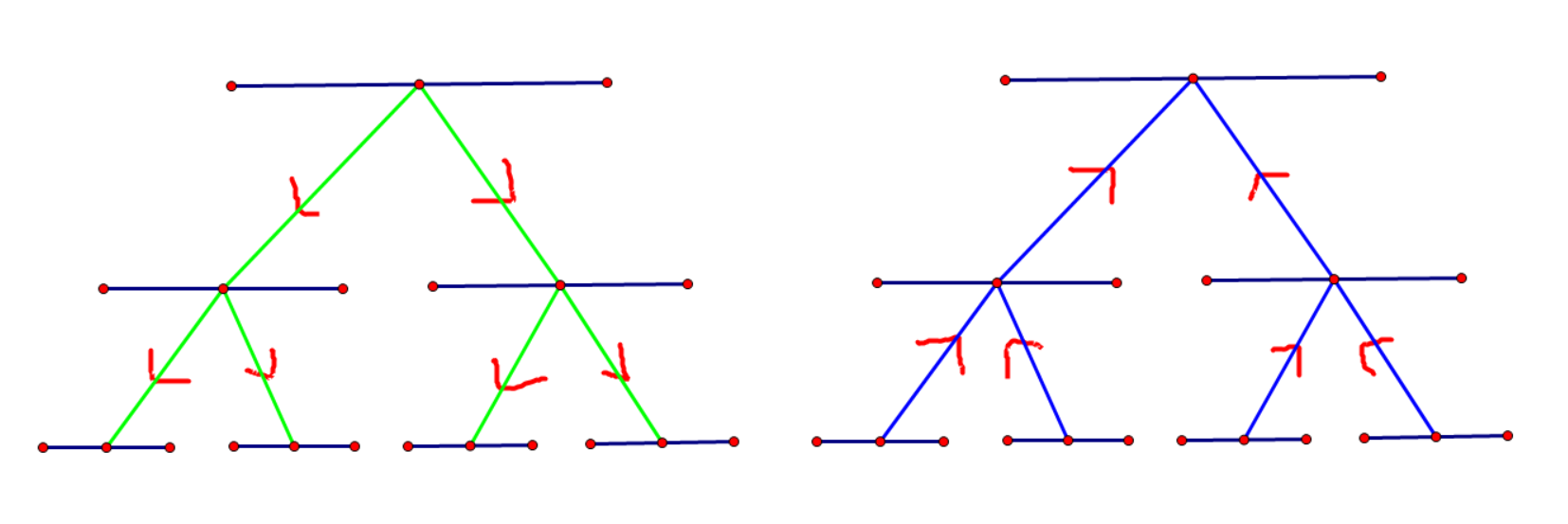
对于2操作,你就从第二课线段树的叶子结点向第一颗线段树中的对应区间连边(下边橙色的边)。
对于3操作,你就从第二课线段树的对应区间向第一课线段树中的叶子结点连边(下边粉色的边)。
其实就是把右边的所有叶节点当做起点,左边的所有点当做起点,我们看能不能到达所有的点。
AC_code
#include<bits/stdc++.h>
#define ios ios::sync_with_stdio(false); cin.tie(0), cout.tie(0)
using namespace std;
using ll = long long;
typedef pair<ll,int> pii;
const int N = 1e5 + 10,M = 1e6 + 10,D = 5e5;
const ll inf = 0x3f3f3f3f3f3f3f3f;
struct Node
{
int l,r;
}tr[N<<2];
int n,m,st;
ll dist[M];
int leaf[N];
bool vis[M];
vector<pair<int,int>> g[M];
void build(int u,int l,int r)
{
tr[u] = {l,r};
if(l==r)
{
leaf[l] = u;
return ;
}
int mid = l + r >> 1;
g[u].push_back({u<<1,0}),g[u].push_back({u<<1|1,0});
g[(u<<1)+D].push_back({u+D,0}),g[(u<<1|1)+D].push_back({u+D,0});
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
}
void connect(int u,int l,int r,int v,int w,int tp)
{
if(l<=tr[u].l&&tr[u].r<=r)
{
if(tp) g[u+D].push_back({v,w});
else g[v].push_back({u,w});
return ;
}
int mid = tr[u].l + tr[u].r >> 1;
if(r<=mid) connect(u<<1,l,r,v,w,tp);
else if(l>mid) connect(u<<1|1,l,r,v,w,tp);
else connect(u<<1,l,mid,v,w,tp),connect(u<<1|1,mid+1,r,v,w,tp);
}
int main()
{
ios;
cin>>n>>m>>st;
build(1,1,n);
for(int i=1;i<=m;i++)
{
int op;cin>>op;
if(op==1)
{
int v,u,w;cin>>v>>u>>w;
g[leaf[v]].push_back({leaf[u],w});
}
else
{
int v,l,r,w;cin>>v>>l>>r>>w;
connect(1,l,r,leaf[v],w,op&1);
}
}
for(int i=1;i<=n;i++) g[leaf[i]].push_back({leaf[i]+D,0}),g[leaf[i]+D].push_back({leaf[i],0});
priority_queue<pii,vector<pii>,greater<pii>> q;
memset(dist,0x3f,sizeof dist);
dist[leaf[st]+D] = 0;
q.push({0,leaf[st]+D});
while(q.size())
{
auto t = q.top();q.pop();
int ver = t.second;
if(vis[ver]) continue;
vis[ver] = 1;
for(auto it:g[ver])
{
int v = it.first,w = it.second;
if(dist[ver]+w<dist[v])
{
dist[v] = dist[ver] + w;
q.push({dist[v],v});
}
}
}
for(int i=1;i<=n;i++)
{
if(dist[leaf[i]]==inf) cout<<"-1 ";
else cout<<dist[leaf[i]]<<' ';
}
}