这次是我第一次参加 \(CSP-J/S\),所以我决定口胡一下这几道题目,由于 \(J\) 组过于简单,就不再叙述,如有问题请私信我 \(/oh /oh /oh\)
假期计划(holiday)
我们可以先进行 \(n\) 次 \(bfs\) 预处理出 \(dis_{i,j}\),表示从 \(i\) 到 \(j\) 的最小转车次数(也就是边权为\(1\)的最短距离再减去\(1\))
由于我们的路径是对称的,所以我们可以看成两条路径 \(1-A-B\) 和 \(1-D-C\),而 \(B,C\) 是否可以到达就判断 \(dis_{B,C} \le k\)
再看到 \(1-A-B\),\(A\) 其实是 \(dis_{1,A} \le k\) 且 \(dis_{A,B} \le k\) 中的最大值,预处理这个最优的决策点为 \(A_1[B]\),同理预处理出第 \(2-3\)优决策点,记为 \(A_2[B]\)、\(A_3[B]\),\(1-D-C\) 也是如此
最后再枚举 \(B,C\),调用 \(9\) 组 \(A_i[B]\) 和 \(D_j[C]\),判断是否重复并计算最大的权值。
时间复杂度 \(O(n^2)\)
策略游戏(game)
贪心,我们可以分析出当先手取得 \(a_i\),后手应该怎样选取才会 \(b_j\) 最小,再逆推回去即可
-
能取异号的,那必然选异号绝对值最大的那个
-
没有异号的,考虑取 \(0\)
-
如果只能取同号的,那么一定取绝对值最小的那个
所以我们可以开 \(6\) 个 \(st\) 表,分别储存 \(a\) 的最大值、最小值、正数最小值、负数最大值(我们可以将 \(0\) 既看成正数,也看成负数,这样就能省去判断是否有 \(0\) 的 \(st\) 表),\(b\) 的最大值以及最小值
得出那六个信息后,我们就可以分情况讨论,也就是 \(A_{l1,r1}\) 中全为正数、负数或者正负都有,\(B_{l2,r2}\) 也是如此,一共 \(9\) 种情况
时间复杂度 \(O(n\) \(log\) \(n)\)
星战(galaxy)
在这里我说一种很简单的方法,随机 \(hash\) 和
我们可以很容易得出,只要每个点的入度为 \(1\),那么必定能构成一个环
所以我们可以给每个点赋一个随机值,记录所有点的点权和为 \(sum\),再记录 \(start_i\) 与 \(pos_i\) 分别表示最初的图的点 \(i\) 在操作之前所有入边对应起点的权值和与操作时进入所有入边对应起点的权值和,这样无论对于哪一个操作都能实现 \(O(1)\) 修改,最后判断 \(\sum_{i=1}^n pos_i\) 是否等于 \(sum\) 即可
时间复杂度 \(O(n)\)
数据传输(transmit)
有两种方法,第一种是记录 \(dp_{i,x,d1,d2}\) 表示从距离点 \(x\) 为 \(d1\) 的点到距离 \(x\) 的 \(2^i\) 祖先为 \(d2\) 的点的最短距离,但写起来有些复杂,这里说一下矩阵乘法 \(+ LCA\) 这种做法
由于 \(k=1\) 是就是树上路径点权和,这启示着我们使用 \(LCA\)
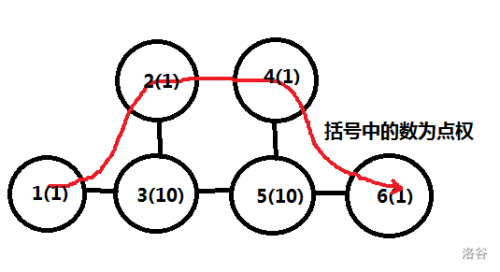
由上图可知,我们选取的点一定是在 \(s-t\) 的路径中的点或它们的临接点,并且跳过的边只会经过一次,例如边 \(1-3\) 和 \(3-2\) 就称为 \(1-2\) 跳过的边(证明私信我)
所以我们令 \(val_i\) 为 \(i\) 的点权,\(nxt_i=min_{(i,j) \in T} val_j\),\(dp_{i,j}\) 表示处理起点到 \(i\) 时,距离 \(i\) 为 \(j\) 的最小值,那么就能直接写出转移石式子,但是会发现会很复杂,处理不当还会影响效率,所以我们使用矩阵乘法优化,重新定义矩阵乘法为 \(c_{i,j}=min(a_{i,k}+b_{k,j})\),就会得到一下矩阵(其中 \(j\) 为 \(i\) 下一个要转移的点)
\[\begin{pmatrix} dp_{i,0} & dp_{i,1} & dp_{i,2} \end{pmatrix} \times \begin{pmatrix} val_j & INF & INF\\ INF & INF & INF\\ INF & INF & INF \end{pmatrix} = \begin{pmatrix} dp_{j,0} & dp_{j,1} & dp_{j,2} \end{pmatrix} (k=1) \]\[\begin{pmatrix} dp_{i,0} & dp_{i,1} & dp_{i,2} \end{pmatrix} \times \begin{pmatrix} val_j & 0 & INF\\ val_j & INF & INF\\ INF & INF & INF \end{pmatrix} = \begin{pmatrix} dp_{j,0} & dp_{j,1} & dp_{j,2} \end{pmatrix} (k=2) \]\[\begin{pmatrix} dp_{i,0} & dp_{i,1} & dp_{i,2} \end{pmatrix} \times \begin{pmatrix} val_j & 0 & INF\\ val_j & nxt_j & 0\\ val_j & INF & INF \end{pmatrix} = \begin{pmatrix} dp_{j,0} & dp_{j,1} & dp_{j,2} \end{pmatrix} (k=3) \]至于为什么是这样就需要根据定义来理解,而且我们不需要关心是哪一个点,只需关心最小值,这我也理解了大半天
起始矩阵大家应该知道吧,这里需要注意一下,因为矩阵没有交换率,所以需要处理 \(up_{x,i}\)(向上)和 \(down_{x,i}\)(向下)两个矩阵,再倍增即可
时间复杂度 \(O(3^3 n\) \(log\) \(n)\)
若没听懂,那就私信我,或者去看这两位大佬的题解 127_127_127 和 Plozia,要代码也可以私信我
CSP-S游记
附一个小游记吧,\(CSP-J\) 的游记不想写了
对于 \(T2\) 想了大半时间,结果第二题更简单,早知道就做第二题了,本来最后还有半个多小时想到正解,但是能了一下优化暴力代码,发现有个样例没过,没办法只能含泪修改暴力。服了 \(T2\),打了一个暴力直接走人,考后发现如此简单,下次必须把所有题目看完再做了。\(T3\) 和第二题一样,根本没想,打了一个 \(multiset\) 优化暴力就走人的。\(T4\) 和第三题一样,也根本没想,打了一个 \(O(n^3)\) 的 \(Floyd\) 走人,连 \(O(n^2)\) 的 \(dp\) 都没打,痛苦。第一次参加比赛,收获还是蛮大的,希望下一次比赛能发挥出我最好的水平
标签:begin,end,val,题解,2022CSP,pmatrix,INF,dp From: https://www.cnblogs.com/duguca/p/16864180.html