魄罗蛙出的noip模拟题
前言
这个题的难度显然没有noip难,魄罗蛙良心出题人
1.二叉树上的询问(erchatree.in/out)
【题目描述】
给出一棵具有 \(n\) 个结点的树。
我们规定,\(1\) 是这棵树的树根。
并且,我们规定,对于所有的 \(2\le i\le n\) ,编号为 \(i\) 的结点的父结点是 \(\frac{i}{2}\) 。
显然,这是一棵二叉树,对于节点 \(i\) ,其左子结点是 \(2i\) ,其右子结点是 \(2i+1\) (如果它有对应子节点的话)。
现在,有 \(m\) 个询问。每个询问,问编号为 \(x\) 的结点在这棵二叉树的前序遍历中排名第几。你需要对每组询问输出对应的答案。
前序遍历:对每棵子树,先访问其根结点,再访问其左子树,最后访问其右子树。
例如,当 \(n=5\) 的时候,前序遍历为 \(\{1,2,4,5,3\}\)
【输入格式】
第一行,输入两个整数 \(n,m\ (1\le n\le 10^{18},\ 1\le m\le 10^5)\),分别表示这棵树的结点总数,以及询问个数。
接下来 \(m\) 行,第 \(i\) 行输入一个整数 \(x_i\ (1\le x_i\le n)\) ,表示询问结点 \(x_i\) 在这棵树前序遍历中的排名。
【输出格式】
对每个询问,输出一行,一个整数,表示对应询问的答案。
【样例】
【输入】
10 5
1
3
5
7
9
【输出】
1
8
6
10
5
【数据范围与提示】
对于 30% 的数据满足, \(n,m\le 10^3\)
对于 60% 的数据满足,\(n\le 10^5\)
对于 80% 的数据满足,\(x_i\le 10^7\)
对于 100% 的数据满足,\(1\le x_i \le n\le 10^{18},m\le 10^{15}\)
有 40% 的数据,\(m=1\)
【时空限制】
1000ms 128MB
分析
考场上的的无脑暴力 \(70pts\)
对于每个节点
若该节点为左儿子,必然是从父节点前序+1得来
若该节点为右儿子,必然是遍历完左儿子后第一个遍历的点
显然右儿子的答案就是父节点编号加上左儿子个数+1
那么问题就变成了求解每个子节点之前点的个数
一颗 \(n\) 层的二叉树有 \(2^n-1\) 个节点,每往下一层就加上该层的节点个数
若统计总数大于实际个数,那么就减去多余的数量即可
#include<bits/stdc++.h>
#define int __int128
using namespace std;
template<typename T>void read(T &x)
{
x=0; char c=getchar(); T neg=0;
while(!isdigit(c)) neg|=!(c^'-'),c=getchar();
while(isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
if(neg) x=(~x)+1;
}
template<typename T>void wr(T x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) wr(x/10);
putchar((x-x/10*10)^48);
return ;
}//快读快写
int m;
int n,x;
int siz(int cat,int now,int real){//统计该节点子树大小 分别表示该点编号 目前大小 本层大小
if(cat>n){return now-min((cat-n),real);}
return siz(cat<<1|1,now<<1|1,real<<1);
}
int num(int sb){//往上递归求答案
if(sb==1)return 1ll;
if(sb&1){return num((sb-1)>>1)+siz(sb-1,1,1)+1;}
else{return num(sb>>1)+1;}
}
signed main()
{
read(n);read(m);
while(m--){
read(x);
int ans=num(x);
wr(ans);putchar('\n');
}
return 0;
}
/*
10 5
1
3
5
7
9
*/
2.追逐(gcd.in/out)
【题目描述】
众所周知,George_Plover chasing death 的缩写是gcd。
同时,gcd又是最大公因数的意思,你需要求出。
\[\prod_{i=a}^b\prod_{j=c}^d gcd(x^{i},y^{j}) \pmod{998244353} \]其中\(\prod\)表示累乘,例如:\(\prod\limits_{i=1}^{n}i=1\times2\times3\times \cdots\times n\)
【输入格式】
输入6个整数,\(a,b,c,d,x,y\)。
【输出格式】
输出⼀⾏,表示题⽬描述式⼦中的计算结果,对 998244353 取余。
【样例】
【样例输入 #1】
1 2 1 2 8 4
【样例输出 #1】
2048
【提示】
【数据范围】:
对于30%的数据,满足\(b,d\leq 1000\)
另有20%的数据,满足\(x,y\)都是质数。
对于100%的数据,\(0\leq a,b,c,d \leq 3×10^{6}\),\(0<x,y<10^{9}\),\(a\leq b,c \leq d\)
【时空限制】
2000ms 256MB
分析
先看 \(x\) 与 \(y\) 互质的情况
显然,不论 \(i\) 与 \(j\) 怎么变,他们的公因数始终为 \(1\)
回到公因数的概念,什么叫公因呐,公因数即是 \(x\ y\) 同种公共因子中最小值的累乘
将 \(x\ y\) 分解质因子
令\(x=2^{c_1}*3^{c_2}*5^{c_3}*....k^{c_x}\)
令\(y=2^{d_1}*3^{d_2}*5^{d_3}*....k^{d_x}\)
则
\(gcd(x,y)=min(2^{c_1},2^{d_1})*min(3^{c_2},3^{d_2})min(5^{c_3},5^{d_3})*...min(k^{c_x},k^{d_y})\)
那么将其扩大到 \(i\ j\) 是也是同一个道理
\(gcd(x^i,y^j)=min(2^{c_1*i},2^{d_1*j})*min(3^{c_2*i},3^{d_2*j})min(5^{c_3*i},5^{d_3*j})*...min(k^{c_x*i},k^{d_y*j})\)
我们需要优化枚举 \(i\ j\) 的效率
在枚举 \(i\) 时,我们发现
如果 此时的因子 \(d_k*j \le c_k*i\) 那之后无论 \(i\) 有多大,该因子的贡献只有 \(k^{d_k*j}\)
那我们可以找到第一个 \(i\) 使得 \(d_k*j \le c_k*i\) 成立,那么 \(j\) 在此时的所有贡献为 \(k^{d_k*j*(c-i-1)}\)
\(j\) 同理
#include<bits/stdc++.h>
using namespace std;
const long long N=5010,P=998244353;
long long a,b,c,d,x,y,prime[N],cnt,cx[N],cy[N],both[N],num,ans=1;
long long vis[40010];
template<typename T>void read(T &x)
{
x=0; char c=getchar(); T neg=0;
while(!isdigit(c)) neg|=!(c^'-'),c=getchar();
while(isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
if(neg) x=(~x)+1;
}
template<typename T>void wr(T x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) wr(x/10);
putchar((x-x/10*10)^48);
return ;
}
void init_()
{
for(long long i=2;i<=40000;++i)
{
if(vis[i]) continue;
prime[++cnt]=i;
for(long long j=2;i*j<=40000;++j)
vis[i*j]=1;
}
}
long long mpow(long long aa,long long bb)
{
long long res=1;
for(;bb;bb>>=1)
{
if(bb&1) res=res*aa%P;
aa=aa*aa%P;
}
return res;
}
int main()
{
freopen("gcd.in","r",stdin);
freopen("gcd.out","w",stdout);
init_();
read(a); read(b); read(c); read(d); read(x); read(y);
long long tx=x,ty=y;
for(long long i=1;i<=cnt;++i)
{
while(tx%prime[i]==0) ++cx[i],tx/=prime[i];
while(ty%prime[i]==0) ++cy[i],ty/=prime[i];
if(cx[i]&&cy[i]) both[++num]=i;
}
for(long long k=1;k<=num;++k)
{
long long sum=0,pk=both[k];
for(long long i=a,j=c;i<=b;++i)
{
while(j<=d&&cx[pk]*i>cy[pk]*j) ++j;
sum+=cx[pk]*i*(d-j+1)%(P-1);
sum%=P-1;
}
for(long long j=c,i=a;j<=d;++j)
{
while(i<=b&&cy[pk]*j>=cx[pk]*i) ++i;
sum+=cy[pk]*j*(b-i+1)%(P-1);
sum%=P-1;
}
ans*=mpow(prime[pk],sum);
ans%=P;
}
wr(ans);
return 0;
}
3.荷塘月色(lotus.in/out)
【题目描述】
在朦胧的月光下面,有 \(n\times m\) 个小池塘,他们排成了 \(n\) 行 \(m\) 列的矩阵。
其中,第 \(i\) 行第 \(j\) 列的小池塘里有 \(a_{i,j}\) 朵荷花 \((1\le i\le n,1\le j\le m)\)。
现在,魄罗蛙计划选出一个子矩阵,将其中的池塘合并在一起,并且希望合并之后的大池塘里恰好有 \(k\) 朵荷花。
现在,魄罗蛙想知道,有多少种不同的选法是满足要求的。
形式化来讲,问存在多少个四元组 $(l_1,r_1,l_2,r_2),\ 1\le l_1\le r_1\le n,1\le l_2\le r_2\le m $ ,满足:
\[\bigg(\sum_{i=l_1}^{r_1}\sum_{j=l_2}^{r_2}a_{i,j} \bigg)= k \]【输入格式】
第一行,输入一个整数 \(T\ (1\le T)\) ,表示数据组数。
接下来,\(T\) 组数据,对每组数据:
第一行,输入两个整数 \(n,m\ (1\le n,m \le 10^5)\) ,表示矩阵的大小。
接下来 \(n\) 行,每行 \(m\) 个整数,第 \(i\) 行的第 \(j\) 个整数为 \(a_{i,j}\ (0\le a_{i,j}\le 10^9)\) 。
接下来一行,输入一个整数,\(k\ (0\le k\le 10^{14})\) ,表示魄罗蛙希望合并的大池塘里的荷花数。
保证对所有的 \(T\) 组数据,\(\sum n\times m \le 2\times10^5\) 。
【输出格式】
输出 \(T\) 行,每行一个整数,分别代表每组数据的答案。
【样例】
【输入】
2
2 2
1 9
0 5
1
5 5
3 1 4 1 5
9 2 6 5 3
5 3 8 4 6
2 6 4 3 3
8 3 2 7 9
19
【输出】
2
7
【数据范围与时空限制】
存在 44% 的数据,满足 \(n\times m \le 2000\)
存在 24% 的数据,满足所有的 \(a_i\) 都是在值域范围随机生成的。
对 100% 的数据,满足题目描述中的数据范围。
【时空限制】
1000ms 128MB
分析
容易想到 \(O(n^{2}m^2)\) 的暴力,枚举每个左上点,枚举每个右下点,维护二维前缀即可
显然我们的矩阵是单调递增的
但我们可以优化用二分优化一维,但感觉过不了,花半天实现不了二维的二分,就打了个\(O(n^{2}m^2)\) 的暴力,最后改为\(O(n^2m\ logn)\)能过
#include<bits/stdc++.h>
#pragma Optimize(2)
using namespace std;
#define MAXN 100001
#define int long long
template<typename T>void read(T &x)
{
x=0; char c=getchar(); T neg=0;
while(!isdigit(c)) neg|=!(c^'-'),c=getchar();
while(isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
if(neg) x=(~x)+1;
}
template<typename T>void wr(T x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) wr(x/10);
putchar((x-x/10*10)^48);
return ;
}
long long kk,ans;
int n,m,T;
signed main() {
read(T);
while(T--)
{
read(n); read(m); ans=0;
int a,sum[n+1][m+1];
memset(sum,0,sizeof sum);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
read(a); sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a;
}
}
read(kk);
if(m>=n)
{
for(int i=1;i<=n;i++)
{
for(int j=i;j<=n;j++)
{
for(int k=1;k<=m;k++)
{
int l=k,r=m,mid=(l+r)>>1,resl=l-1,resr=m+1;
while(l<=r)
{
mid=(l+r)>>1;
int now=sum[j][mid]-sum[j][k-1]-sum[i-1][mid]+sum[i-1][k-1];
if(now<kk) l=mid+1,resl=mid;
else r=mid-1;
}
l=k; r=m;
while(l<=r)
{
mid=(l+r)>>1;
int now=sum[j][mid]-sum[j][k-1]-sum[i-1][mid]+sum[i-1][k-1];
if(now>kk) r=mid-1,resr=mid;
else l=mid+1;
}
ans+=resr-resl-1;
}
}
}
}
else
{
for(int i=1;i<=m;i++)
{
for(int j=i;j<=m;j++)
{
for(int k=1;k<=n;k++)
{
int l=k,r=n,mid=(l+r)>>1,resl=l-1, resr=n+1;
while(l<=r)
{
mid=(l+r)>>1;
int now=sum[mid][j]-sum[k-1][j]-sum[mid][i-1]+sum[k-1][i-1];
if(now<kk) l=mid+1,resl=mid;
else r=mid-1;
}
l=k; r=n;
while(l<=r)
{
mid=(l+r)>>1;
int now=sum[mid][j]-sum[k-1][j]-sum[mid][i-1]+sum[k-1][i-1];
if(now>kk) r=mid-1,resr=mid;
else l=mid+1;
}
ans+=resr-resl-1;
}
}
}
}
wr(ans);putchar('\n');
}
return 0;
}
4.光华楼(fdu.in/out)
【题目描述】
光华楼很高。
现在给出楼层编号 \(0\) ~ \(m\)。
某位大佬想到了一种传送方式。
楼层 \(x\) 对应一个传送目标 \(y\)(即从编号为 \(x\) 的楼层进行传送,则会传送到编号为 \(y\) 的楼层):
1.如果 \(x\) 是奇数,那么 \(y=(x-1)/2\)
2.如果 \(x\) 是偶数,那么 \(y=(x/2)+2^{n-1}\)
可以发现,通过这种传送方式,从 \(x\) 出发,不断传送,貌似传送几次后会回到 \(x\) 。于是他把从一个编号为 \(x\) 的楼层出发,第一次回到 \(x\) 时经历的传送次数称为 \(f(x)\)。
特殊的,如果从 \(x\) 出发永远不能回到 \(x\) ,那么 \(f(x)=0\) 。
现在,你需要求出 \(\sum_{i=0}^m f(i) \mod 998244353\) 的值。
由于 \(m\) 的值可能很大,所有的输入中,\(m\) 以一个 \(n\) 位的二进制数的形式输入(保证有 \(n\) 位,可以有前导 \(0\) )
【输入格式】
输入共两行。
第一行,整数 \(n\) 。
第二行,一个二进制整数 \(m\) 。
【输出格式】
一行,一个整数, 答案对 \(998244353\) 取模的结果。
【样例 #1】
【样例输入 #1】
3
111
【样例输出 #1】
40
【样例 #2】
【样例输入 #2】
6
110101
【样例输出 #2】
616
【提示】
样例1解释:
\(m=7\),
\(f(0)=6,\\f(1)=6,\\f(2)=2,\\f(3)=6,\\f(4)=6,\\f(5)=2,\\f(6)=6,\\f(7)=6\)
求和后 \(M=40\)
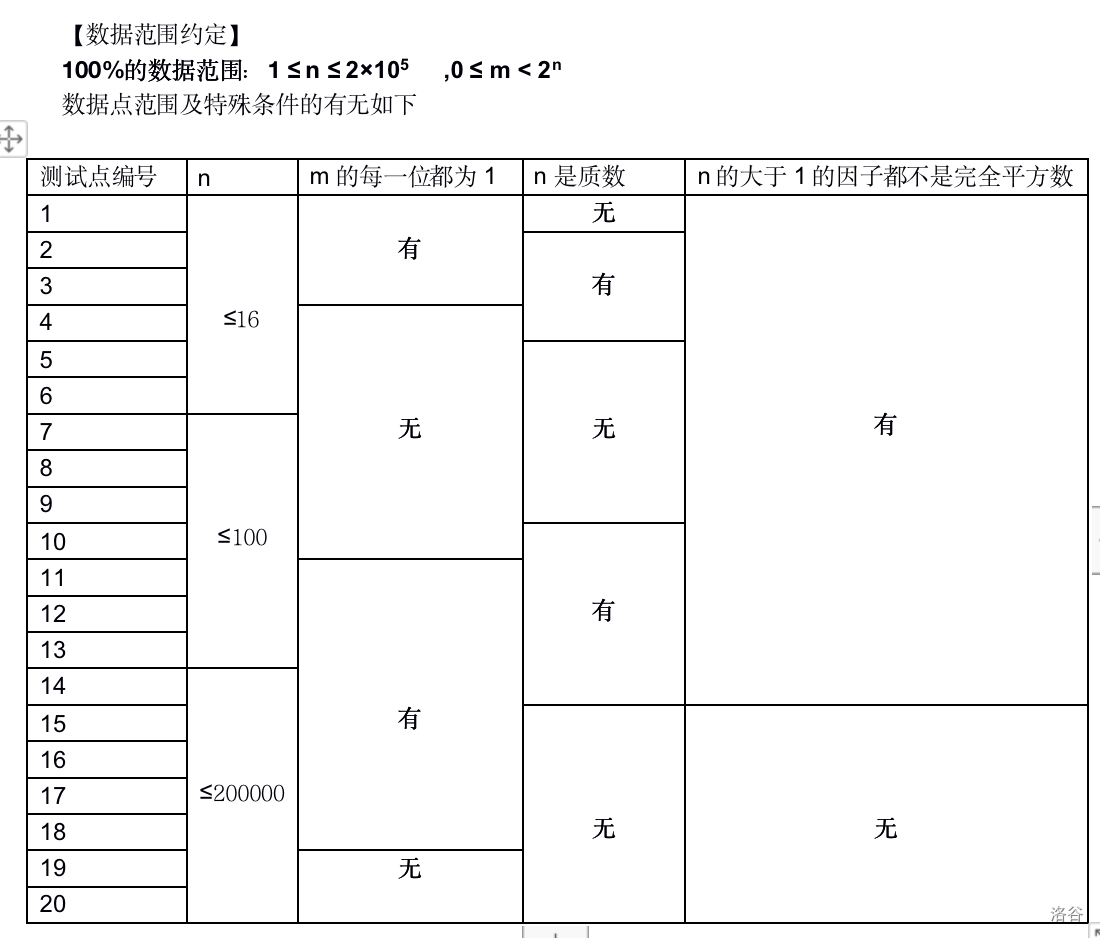
【时空限制】
1000ms 256MB
分析
不会,暴力30
#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#define int long long
using namespace std;
const int maxn = 300000;
const int mod = 998244353;
template<typename T>void read(T &x)
{
x=0; char c=getchar(); T neg=0;
while(!isdigit(c)) neg|=!(c^'-'),c=getchar();
while(isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
if(neg) x=(~x)+1;
}
template<typename T>void wr(T x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) wr(x/10);
putchar((x-x/10*10)^48);
return ;
}
int n,bit[maxn],m,c,k,Ans;
char s[maxn];
int lim=10000;
__int128 ANS,K,N,MOD=__int128(998244353);
bool prim(int x)
{
for(int i=2;i*i<=x;i++) if(!(x%i)) return 0;
return 1;
}
signed main()
{
// freopen("fdu.in","r",stdin);
// freopen("fdu.out","w",stdout);
read(n);
if(n>=32)
{
if(prim(n))
{
K=__int128(n*2);
ANS=(((K*(1<<n)%MOD)%MOD-__int128(2*(n*2-2)))%MOD+MOD)%MOD;
wr(ANS);
return 0;
}
K=__int128(n*2);
wr(((K*((1<<n)%MOD))%MOD+MOD)%MOD);
return 0;
}
k=(1<<(n-1));
scanf("%s",s+1);
int len=strlen(s+1);
for(int i=1;i<=n;i++) c=s[i]-'0', bit[n-i]=c;
for(int i=0;i<n;i++) m|=(bit[i]<<i);
for(int i=0;i<=m;i++)
{
int st=i,tim=1;
if(st&1) st=(st-1)>>1;
else st=(st>>1)+k;
while(st!=i)
{
// cout<<st<<" ";
if(tim>=lim) {tim=0; break; }
if((st&1)) st=(st-1)/2,tim++;
else st=(st>>1)+k,tim++;
}
// cout<<tim<<"!"<<endl;;
Ans=(Ans+tim)>=mod?(Ans+tim-mod):Ans+tim;
}
wr(Ans);
return 0;
}
/*
3
111
6
110101
16
11111011101111111
*/