【N】新本格魔法少女
好题分享
1月6日好题分享-安师大附中 - Virtual Judge
P11365 [Ynoi2024] 新本格魔法少女りすか - 洛谷
这是一道卡常分块题。
直接对序列分块,则计算贡献分为如下情况:(不妨设块长为 \(B\))
- 散块对散块:直接用树状数组统计顺序对,复杂度 \(O(nB\log n)\)。
- 整块对其他:因为该题空间较小,所以考虑逐块处理。讨论第 \(i\) 块对答案的贡献时,可以扫描线 \(j\) 维护第 \(i\) 块与前缀 \(j\) 产生的贡献。维护时可以考虑开桶并后缀和。加到答案上时要容斥一下。后缀同理。复杂度 \(\displaystyle O(\frac{n^2}{B})\)。
平衡后,总复杂度为 \(O(n\sqrt{n\log n})\)。如果使用压位树状数组,那么复杂度可以写成 \(O(n\sqrt{n(\log n-\log w)})\)。
压位 BIT
为了卡常,本题使用了压位树状数组。它基于一个性质:
- 维护的数组值域很小。
这个方法能让树状数组单点修改、查前缀和的复杂度变为 \(\displaystyle O(\log\frac{n}{w})\),即 \(O(\log n-\log w)\)。
例如,维护的数组值域为 \(\{0,1\}\) 时(本题),可以把每 \(w\)(\(w=64\))个数组的位置分为一组,用树状数组维护它们的和,并且还要维护每组每个位置的值,可以用二进制数,来支持区间查询(掩码 + \(O(1)\) popcount)。
BIT 清空减枝
加速树状数组清空的方法好用的有如下两个。
首先,是把所有操作记录下来,单次操作记录时空复杂度为 \(O(1)\)。
清空时,把操作经过的位置清零,但是,有如下减枝:
- 当一个位置已经清零时,直接退出。
这使得清空复杂度变为 \(O(\min(n,q\log n))\)(\(n\) 为数组大小,\(q\) 为操作次数)。
正确性证明可以考虑把清空弱化为减法。
下面是代码:
Tp c[SIZE1]; int N;
int mem[SIZE2], mcnt;
void clear() {
for (int i = 1; i <= mcnt; i++) {
for (int it = mem[i]; it <= N; it += it & -it) {
if (c[it] == 0) break;
c[it] = 0;
}
}
mcnt = 0;
return ;
}
其次还有个办法,就是记录每个位置最后一次被更新的时间,如果这个时间少于清空的时间,则清空这个位置。清空的复杂度为 \(O(1)\)。不过慢一些。
实际上,暴力 \(O(n)\) 清空 BIT 是非常快速的。所以为了卡常,可以在操作次数大于 \(T\) 时暴力单次 \(O(n)\) 清空。
在本题中,\(T\) 可以是 \(650\)。
C++98 的速度
在本题中,C++98 的速度薄纱 C++20 的。可能在一些 OJ 上可以用这个来卡常。
【N】Decinc Dividing
好题分享
1月6日好题分享-安师大附中 - Virtual Judge
Submission #300005583 - Codeforces
一道 dp 题。做法高度依赖 dp 值域的性质。
这题要对合法的区间 \([l,r]\) 计数,而合法的区间是能划分为上升子序列和下降子序列的区间,发现当 \(l\) 被固定时,合法的 \(r\) 为一段区间,而且 \([l,l]\) 合法,所以可以考虑求出所有 \(l\) 的最大的 \(r\)。
设 \(f_{i,j}\) 表示区间 \([l,i]\) 中 \(a_i\) 被划分到上升子序列中,下降子序列的最后一个数为 \(j\),能否合法。也对称的设 \(g_{i,j}\)。对于一个区间 \([l,r]\),复杂度是 \(O(n(r-l+1))\) 的。
因为 dp 值都是布尔值,所以考虑在 dp 值上记录更多信息。发现对于 \(f_{i,j}=\text{true}\) 的情况,对于一个 \(i\),希望 \(j\) 越大越好,所以可以重定义 \(f_i\) 表示区间 \([l,i]\) 中 \(a_i\) 被划分到上升子序列中,下降子序列在合法的情况下,最大能是多少。\(g_{i,j}\) 同样这么重定义。这样对于一个区间 \([l,r]\),复杂度为 \(O(r-l+1)\)。
容易发现,极大合法区间 \([l,r]\) 的 \(r\) 随着 \(l\) 单调不降,所以考虑双指针。发现 \(f_i\) 在 \(l\) 变化的情况下,可能的值只有 \(O(1)\) 个 [1] 。所以可以暴力更新 dp 数组,不过,当没有产生变化时,直接减枝。最后复杂度就是 \(O(n)\) 了。
因为该题的限制很严,所以可以感受出性质 [1]。若要证明其正确性,可以考虑最大的 \(j\) 满足 \(j<i\) 且 \(a_{j}>a_{j+1}\)。此时,\(a_j\) 和 \(a_{j+1}\) 不能同时在上升序列中,故必有至少一个在下降序列中;而因为 \(j\) 的最大性,其一必然为下降序列的结尾。综合其他较为平凡的情况(如找不到 \(j\)),可得 \(f_i\in\{a_j,a_{j+1},\inf,-\inf\}\)。
【H】Graph Weighting
1月6日好题分享-安师大附中 - Virtual Judge
Graph Weighting Editorial - 洛谷专栏
点双连通分量 + 决策单调性题。
点双连通分量和生成树是密切相关的**。首先发现每个点双内边的权值必须相等。
然后,问题就能够被转化为非线性规划问题。
发现约束条件中系数相同的项可以分开求解,而系数至多有 \(O(\sqrt n)\) 种。每一类可以用优先队列贪心,因为调和级数,这部分复杂度为 \(O(n\log^2n)\)。
把每一类的结果合并时,是 \(\min+\) 卷积。由于合并的一边具有凸性和单调性,所以相当于决策单调性优化 dp。总复杂度就是 \(O(n\sqrt n\log n)\)。
如果合并使用 smawk 算法,可以做到优秀的单次 \(O(n)\),总复杂度变为 \(O(n\log^2n+n\sqrt n)\)。
本题的易错点:决策单调性分治时,为了保证决策点的正确性,不能简单的在凸性函数末尾补 \(\inf\),这可能会损坏其凸性。
用点双划分边
在本题中,需要算出每个点双的点数和边数。
虽然可以直接建圆方树,但是有隐式建树的方法。
首先,有如下显然的性质:
- 一个点可能同时属于多个点双。
- 一条边连接的两点一定属于同一个点双。
- 一条边恰好属于一个点双。
然后容易发现:
- 若将所有点双中深度最小的点剔除,那么每个点恰好属于一个点双。
上面等价于把圆方树中所有圆指向其父节点。
于是,就可以用 tarjan 求出所有点如上属于的点双。对于边 \(u\leftrightarrow v\),不妨设 \(\text{deep}(u)<\text{deep}(v)\)(\(\text{deep}\) 表示该节点在 dfs 树上的深度),那么该边属于 \(v\) 所属的点双。
有凸性的非线性规划问题
有时,可能遇到如下问题。
你需要最小化目标函数 \(z\):(\(\forall i\),\(f_i\) 是函数,\(x_i\) 是变量,\(n\) 为变量个数)
\[z=f_1(x_1)+f_2(x_2)+\cdots+f_n(x_n) \]但要满足约束:(\(C\) 是一个常数)
\[\begin{gathered} x_1+x_2+\cdots+x_n=C\\ x_1,x_2,\dots,x_n\geq 0 \end{gathered} \]但是其满足一个重要性质:\(\forall i\),\(f_i(x)\) 的导数(或差分)随 \(x\) 单调不降。
这使得局部最优解就是全局最优解。
下面,不妨设 \(x_0\),\(f_i(x_0)\),\(\displaystyle\frac{\mathrm{d}}{\mathrm{d}x_0}f_i(x_0)\)(或者 \((\nabla f)(x_0)\))的互相计算是 \(O(1)\) 的。
优先队列贪心
如果变量的值域离散,那么可以考虑使用优先队列贪心。时间复杂度 \(O(C\log n)\)。
二分斜率
使用该方法的要求是,\(\forall i\),如果知道 \(\displaystyle\frac{\mathrm{d}}{\mathrm{d}x_0}f_i(x_0)\),能快速计算 \(f_i(x_0)\)。不妨设这部分时间复杂度为 \(O(T)\)。
如果变量的值域连续,则有性质,当 \(z\) 最优时,存在方案使得
\[\frac{\mathrm{d}}{\mathrm{d}x_1}f_1(x_1)=\frac{\mathrm{d}}{\mathrm{d}x_2}f_2(x_2)=\cdots=\frac{\mathrm{d}}{\mathrm{d}x_n}f_n(x_n) \]设其为 \(k\),则可二分它,然后再判断是否符合其他要求。时间复杂度 \(O(n\log V)\)(\(V\) 为导数的取值范围)。
如果变量的值域是离散的,那么就需要在二分斜率后再跑优先队列贪心。因为差分可能有 \(\pm 1\) 的差距。复杂度 \(O(n(\log V+\log n))\)。
一边有凸性的 \(\min +\) 卷积。
一边有凸性的 \(\min+\) 卷积可以用决策单调性优化 dp 单 \(\log\) 解决。还有一些相关算法:
- 闵可夫斯基和:两边都凸,线性。
- smawk 算法:该问题线性。
四边形不等式性
下文中的 \(+\) 可能不是传统意义上的加法。
若 \(a<b\),则定义 \(a\) 优于 \(b\)。
定义:如果二元函数 \(w(x,y)\) 满足 \(\forall x_1\leq x_2\leq x_3\leq x_4\),
\[w(x_1,x_3)+w(x_2,x_3)\leq w(x_1,x_4)+w(x_2,x_3) \]那么称其有四边形不等式性。
也可以写为:
\[\begin{gathered} \forall x<y\\ w(x,y)+w(x-1,y-1)\leq w(x-1,y)+w(x,y-1) \end{gathered} \]或者写成差分形式:
\[\nabla_x\nabla_yw(x,y)\leq 0 \]区间包含单调性的定义:若函数 \(w(x,y)\) 满足 \(\forall x_1\leq x_2\leq x_3\leq x_4\)
\[w(x_2,x_3)\leq w(x_1,x_4) \]则称其有区间包含单调性。
实际上,这相当于
\[\left\{ \begin{gathered} \nabla_xw(x,y)\leq 0\\ \nabla_yw(x,y)\geq 0 \end{gathered} \right. \]可能平凡性:下面几个关于 \(x,y\) 的函数都满足四边形不等式
- \(C\)(\(C\) 是常数)
- \(f(x)\)(\(f\) 是一个函数。也有对称结论 \(g(y)\))。
- \(f(x)+g(y)\)(\(f\) 和 \(g\) 都是函数)
而且它们在四边形不等式中一定取等。
可进行线性运算性:对于满足四边形不等式的函数 \(w_1(x,y),w_2(x,y)\),
\[k_1w_1(x,y)+k_2w_2(x,y)+C \](其中 \(k_1,k_2\geq 0\),\(k_1,k_2,C\) 均为常数)也满足。
与单调凸函数复合:
这里的凸指的是导数单调不降。
| \(h(x)\) | \(w(x,y)\) | \(h(w(x,y))\) |
|---|---|---|
| 单调不降,凸 | 区间包含单调性,四边形不等式 | 区间包含单调性,四边形不等式 |
| 凸 | 区间包含单调性,四边形恒等式 | 四边形不等式 |
没有找到比较牛的证明。可以使用偏导感性理解。没有完成的证明 - Note.ms 末尾有证明 - OI Wiki
决策单调性优化 dp 的取点问题
在分治或二分队列求解策单调性优化 dp 问题时,如果有多个同样优的决策点,应该取那个呢?
实际上,可以将决策点的位置作为第二关键字来比较决策点是否优,这样就能避免这种情况(有多个同样优的决策点)的发生。
通常而言,我们会
- 取最左边的决策点
- 或取最右边的决策点
这都是对的。
这个做法是错误的:无规则地取决策点。
【E】跳棋 draughts
模拟赛的题。
发现限制很奇怪,而且是从左往右跳。然后就能发现性质,如果不管左右边界,那么奇偶性相同的跳跃位置单调不降。证明可以直接用其定义式。
于是用线段树和分讨就能做到 \(O(n\log n)\)。
有一个小技巧,可以不二分第一个到达 \(L\) 的跳跃,因为可以直接硬算到底,然后判断是否超过 \(L\)。
【N】套娃
模拟赛的题。
发现两个性质:
- 合并的两个区间值域不交。
- 是否可以合并,具有子序列包含单调性。
然后可以推广出一个结论:
- 如果存在大小关系为 \(2,4,1,3\) 之类的子序列,则该区间一定不可能被合并。其实这还是充要条件。
然后用 rmq 和值域 BIT 维护每个左端点的最长可合并区间,对于查询,预处理倍增数组即可。最终复杂度 \(O(n\log n)\)。
【N】挑战 NPC III
来自好题分享。
搜索题。
先把重边去了。
首先,将题意转化为
- 对大小为 \(k\) 的点覆盖计数。
然后,考察度数较大的点,发现性质
- 度数大于 \(k\) 的点必须选。
然后,把这些点删掉,剩下的点的度数每个不超过 \(k\);选一个点最多覆盖 \(k\) 条边,最多选 \(k\) 个点,于是最多有 \(k^2\) 条边。
然后,设计一种搜索,在 dfs 的每一层都至少选一个点,这样搜索深度就不超过 \(k\)。然后复杂度就是 \(O(\mathcal{T}(k)\operatorname{poly}(k))\)(\(\mathcal{T}(k)=2\mathcal{T}(k-1)+\mathcal{T}(k-2)\))。
需要注意的是,搜索的终点要算组合数,否则就是 \(O(\) 答案 \()\) 的复杂度了。
【E】Łamigłówka
来自好题分享。
1月10日好题分享-学军中学 - Virtual Judge
P9262 [PA 2022] Łamigłówka - 洛谷
首先,进行 \(O(1)\) 次操作让方格到角上。
然后维护它在哪个角,而暂不真的进行操作。这样就能让操作简化为转圈了。
发现每转一圈形状不变,但是把方格进行了置换。
直接求出置换,然后把每个置换环转几下就做完了。
复杂度 \(O(nm+k)\)。
如果后边置换的部分用倍增,那么复杂度为 \(O(nm\log k)\)。
小心转置换环不要写挂。
【H】Histogram Rooks
Submission #61526564 - AtCoder Grand Contest 041
[AGC041F] Histogram Rooks - 洛谷
一道爆标计数题,需要对容斥有清醒的认识。
首先把广义笛卡尔树 \(O(n^2)\) 建了。


放棋子的方案合法的充要条件为:
- 每一列的每一格都能被棋子控制。
为了方便计数,我们记录如下状态:
- 恰好属于集合 \(S\) 的列最后是没放棋子的。
在树形 dp 时,设这一小行长度为 \(L\),属于 \(S\) 的列的个数为 \(t\),则我们希望贡献为
\[\begin{cases} 2^L & (t=0)\\ 2^{L-t}-1 & (\text{otherwise}) \end{cases} \]但是这不能保证剩下的 \(L-t\) 列中一定有棋子,所以考虑容斥,再钦定 \(u\) 行是空的。
在 dp 是,我们记 \(f[i][j][0/1]\) 表示在 \(i\) 节点,有 \(j\) 列因为某种原因是空的(属于 \(S\) 集合或被钦定),是否全是钦定的列。
需要注意的是,要把容斥系数直接放入 dp 中。
因为树上背包复杂度是 \(O(n^2)\) 的,所以这题可以做到 \(O(n^2\log n)\) 的复杂度。
广义笛卡尔树和直方图刨分
见上。
树上背包复杂度
由于每两个点之间至多合并 \(O(1)\) 次,所以复杂度为 \(O(n^2)\)(\(n\) 为树的节点个数)。
实现时,要写上下界优化。
容斥是用来干什么的
容斥本来的作用是
- 放宽问题的某些限制。
但是它会带来糟糕的
- 容斥系数和更多计数问题(例如,需要计算更多集合的大小来算出一个集合的大小)。
所以贪心的来讲,能不容斥就不容斥。
不过容斥还能带来一个附加好处:
- 让某些限制变严。
有时候,更严的限制反而更好计算。不过,如果单纯的为了得到这一好处,应该选择直接
- 增加状态。
通常它只会带来复杂度的增加这一坏处。
【E】Odd Mineral Resource
主席树哈希题或者树上莫队分块题。
主席树 Submission #300625666 - Codeforces
莫队 Submission #300784140 - Codeforces
主席树的做法简简单单。时间复杂度 \(O(n\log n)\)。
莫队做法的话,如果使用树状数据结构维护,时间复杂度将多一个 \(\log n\),会被卡掉。所以,要使用分块平衡复杂度。
实际上,只需要开一个桶,维护每个值出现次数是否是奇数,并且对桶分块,维护每个块出现次数是奇数的值的个数即可。
最终复杂度 \(O(n\sqrt n)\)。
主席树的准确空间
在本节中,主要探讨递归建树时,线段树的节点数和深度与维护数组大小的关系。
建树的代码如下:
- 函数 \(\text{build}(l,r)\)
- 新建一个节点
- 如果 \(l<r\) 则
- 令 \(\displaystyle \text{mid} = \lfloor\frac{l+r}{2}\rfloor\)
- 递归调用 \(\text{build}(l,\text{mid})\)
- 递归调用 \(\text{build}(\text{mid}+1,r)\)
在本节中,默认要维护的数组为 \(a[1],a[2],\dots,a[n]\),一个节点所维护的数组为 \(a[l],a[l+1],\dots,a[r]\)
长度定理:对于线段树的一个节点,若其代表线段的长度为 \(\text{len}\)(\(\text{len}=r-l+1\)),则其左儿子代表线段的长度为 \(\displaystyle \lceil\frac{\text{len}}{2}\rceil\),右儿子代表线段的长度为 \(\displaystyle \lfloor\frac{\text{len}}{2}\rfloor\)。
节点数猜想:线段树的节点个数为 \(2n-1\).
详情:设节点数为 \(\text{cnt}(n)\),则可得 \(\text{cnt}(1)=1\),\(\displaystyle \text{cnt}(n)=\text{cnt}(\lceil\frac{n}{2}\rceil)+\text{cnt}(\lfloor\frac{n}{2}\rfloor)\),可以使用程序 \(O(n)\) 验证。实际上,当 \(n\leq {10}^8\) 时,该猜想正确。感觉这个猜想应该时对的,可能归纳可以证明。
树高猜想:线段树的树高为 \(\lceil\log_2 n\rceil+1\). 设树高为 \(h(n)\),则 \(\forall i<j\) 有 \(h(i)\leq h(j)\)。
详情:有 \(h(1)=1\),\(\displaystyle h(n)=\max\{h(\lceil\frac{n}{2}\rceil),h(\lfloor\frac{n}{2}\rfloor)\}+1\)。也可以 \(O(n)\) 验证。实际上,当 \(n\leq 10^{8}\) 时,该结论成立。
下文中,默认主席树只有单点修改操作。设修改次数为 \(q\)。
主席树推荐空间:为 \(\text{cnt}(n)+qh(n)\),即为 \(2n+q(\lceil\log_2 n\rceil+1)\)。不过很多地方都推荐开 \(32n\) 或 \(40n\).
卡满主席树空间:每次修改都修改 \(a[1]\) 即可。这基于上文的树高猜想。
树上莫队(伪)
如果是子树查询,则可将树变为 dfs 序,如果是路径查询,则可将树变成括号序。
如果是括号序,就需要在指针扫描时,记录一个节点在区间中出现了几次,如果是偶数次,则相当于 \(0\) 次。有的时候还需要暂时添加。
由于 lca 的特殊性,查询区间时要分类讨论。设节点 \(i\) 的左括号位置为 \(F(i)\),右括号位置为 \(L(i)\),则对于 \(x,y\) 路径的查询:
- 令 \(F(x)\leq F(y)\)
- 若 \(\text{lca}(x,y)=x\) 则
- 查询区间为 \([F(x),F(y)]\)。
- 否则
- 查询区间为 \([L(x),F(y)]\) 并 \(\text{lca}(x,y)\) 所在位置。
【N】A Independent Set
Submission #61660677 - AtCoder Grand Contest 066
[AGC066D] A Independent Set - 洛谷
一道“小贪心” dp 题。
为了防止分讨,令 \(S[n]=\texttt{B}\).
考虑对 \(S\) 操作后得到的串 \(T\),如果操作方式是最优的,那么 \(T\) 一定能被划出若干个段
\[[l_1,r_1],[l_2,r_2],\dots,[l_k,r_k] \]满足 \(\forall i\),\(T[l_i:r_i]=\texttt{ABAB}\cdots\texttt{AB}\);不属于任何一段的字符一定是 \(\texttt{B}\)。
然后,又能发现一个性质,用以序列划分 dp:
- \(\forall i\),\(T[l_i:r_i]\) 的字符均来自于 \(S[l_i:r_i]\)。
那么,考虑如何计算 \(S[l:r]\) 变为 \(T[l:r]\) 的代价。设序列 \(X\) 的前缀和为 \(\text{pre}\),则能发现,将 \(i\) 位置的字符挪动至 \(j\) 位置所花费代价为
\[|\text{pre}(i)-\text{pre}(j)| \]又发现,可以使用转移方式使得绝对值正负性不变。于是,使用一些杂乱的线性技术可做到 \(O(n)\)。
“最优值易算”现象
该题目中出现了一个现象,就是,当使用最优子结构转移 dp 时,区间的贡献变得易于计算了(没了绝对值)。
这可能是一个常见的现象。
一个其他领域的例子是,高中物理的机车启动问题中,机车功率不变时,当时间最优(速度最大)时,车速是多少。实际上,速度最大值比任意时间速度好算很多。
【E】BFS Trees
简简单单图论小计数。
Submission #300926394 - Codeforces
[AGC067D] Unique Matching - 洛谷
考虑对于每两个点 \(x,y\) 求一次答案。
首先,有性质
- \(x\) 和 \(y\) 间的最短路唯一,否则答案为 \(0\)。
然后先把最短路当作树边。
然后,不妨先将所有剩下的边拆成两条有向边,对于所有边 \(u\to v\),满足(\(d\) 为距离函数)
\[\begin{cases} d(x,u)+1=d(x,v)\\ d(y,u)+1=d(y,v) \end{cases} \]的话,就把他当成树边。
正确性显然。容易做到单次 \(O(m)\)。总复杂度为 \(O(n^2m)\)。
【N】Unique Matching
dag 形递归计数题。难点在于如何找到可递归的结构。
使用任意模数一定程度上“卡掉”了分治 NTT,放过了暴力。
Submission #61676449 - AtCoder Grand Contest 067
[AGC067D] Unique Matching - 洛谷
zhiyin123 的题解:AT_agc067_d [AGC067D] Unique Matching - 洛谷专栏
反向思考
对于有很强对称性的题(如置换问题,线性规划问题,网络流问题等),如果一种想法失败了,其对偶的想法可能很有前途。
难度变更
难度降级一次。
【E】Qingshan and Daniel
诈骗题。
Submission #301074016 - Codeforces
首先,确定一个必输队,然后,对于必输队的每一张牌,执行操作
- 找到离他最近的异队牌,删掉。
最后就是答案。
该做法的正确性证明很简单。
时间复杂度 \(O(n)\)。
另外,这题不是模拟题。
【N】LIS and Inversion
纯粹的 dp 题。
Submission #61719813 - AtCoder Regular Contest 180
[ARC180E] LIS and Inversion - 洛谷
发现没思路,于是直接 dp。但是也不好做,不妨只研究代价为 \(0\) 的情况。设 \(f[i][j]\) 表示,\(i\) 的排列,代价用长为 \(i\) 的 \(a\) 的前缀计算,其中一个上升子序列的末尾有 \(j\) 个数比它大。
于是写出转移
\[f[i][j]=\max \begin{cases} \max\limits_{k\geq j} f[i-1][k] & (j\geq a_i)\\ f[i-1][j-1] & (j-1\geq a_i)\\ f[i-1][j] \end{cases} \]通过贪心和单调性,将转移简化为
\[f[i][j]=f[i-1][j]+[j\geq a_i] \]然后,贪心和整体 dp 就能解决此问题了。
实现精细复杂度 \(O(n)\),粗糙为 \(O(n\log n)\)。
基于算法结构的思考
一个很常见的思考方式是
- 直接套上一个算法(常见的有 dp、搜索、线段树、分块等),然后思考和优化。
在没思路是可以尝试。
【N】Squares
数据结构维护最短路题。
扫描线做法 Submission #301226041 - Codeforces
“广义”线段树做法 Submission #301312949 - Codeforces
首先,通过考察询问产生的变化,把问题转化为
- 求 \(O(q)\) 次任意两点之间最短路。可以离线。
然后,发现 B 类边越过的区间不交。(使用一些简单的不等式容易证明)
于是,就可以使用
- 扫描线 + 数据结构
维护了。能做到 \(O(n\log n)\)。
也可以把区间形成的线段树建出来,然后使用 lca 等技术完成求解。时间复杂度为 lca 复杂度。
给一些区间建线段树
方法一:使用递归建树。对于所有区间 \([l,r]\),建立点 \(l\) 和点 \(r\),并连边 \(l\to r\),然后就可以快速跨国一个区间了。使用一些手段可以做到线性。
方法二:模拟递归建树。把所有区间以 \((l,-r)\) 为关键字升序排序,然后用栈来维护森林的根。容易做到 \(O(n\log n)\),不过也能做到线性。
【H】Three View Drawing
神秘 ad-hoc 构造题。
Submission #61743887 - AtCoder Regular Contest 175
[ARC175E] Three View Drawing - 洛谷
这题和拉丁方阵有关。
如下图构造
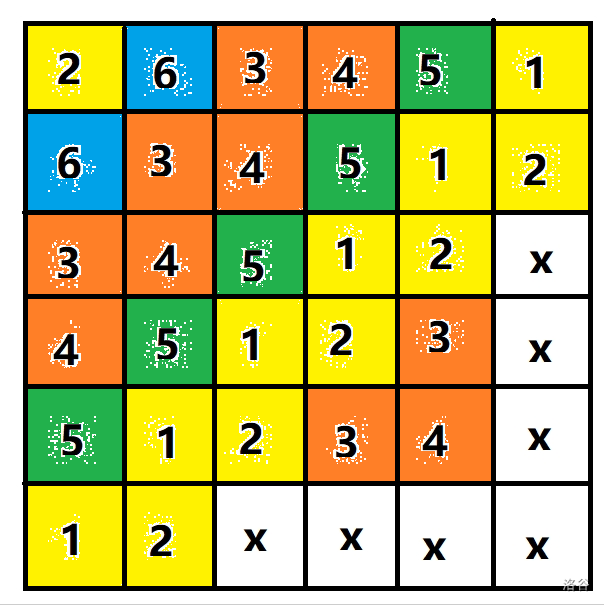
【N】Subset Trick
数据结构题。
Submission #301381212 - Codeforces
首先,将 \(S\) 从小到大排序。
通过一些转化,题目变成求一些区间的并的大小。
发现区间是否交叉具有凸性和对成性(不等式易证)。然后就可以拆贡献算了。
最后复杂度 \(O(n\log^2n)\)。
其中有个细节,凸包的顶端为对称轴,所以不需要三分。
【H】Avoid Boring Matches
借助了全局最劣解进行的贪心。
Submission #61763990 - estie Programming Contest 2023 (AtCoder Regular Contest 169)
[ARC169E] Avoid Boring Matches - 洛谷
首先,判掉无解情况。(\(\texttt A\) 比 \(\texttt B\) 少)
对于确定的 \(S\),使用贪心法从左到右确定第一轮的配对情况。
然后,通过交换和归纳的方法说明:
- 局部最劣解就是全局最劣解。
然后,在用类似的方法找到全局最劣解 \(T\)。
为了计算答案,把 \(\texttt A\) 刻画成 \(-1\),\(\texttt B\) 刻画成 \(1\),然后,要求 \(S\) 的每一个前缀和大于(非严格)对应 \(T\) 的。
因为每次交换差分都会让仅一个前缀和增加 \(2\),所以答案就容易计算了。
通过最劣解判断
在判断性问题中,可以使用全局最劣解判断其他解是否合法。
实际上,这是一种贪心思想。
交换差分模型
这是一个小练习。
给定长度为 \(n\) 的序列 \(a\) 和 \(b\),其中 \(\forall i\),\(a_i,b_i\in\{-1,1\}\)。你需要对 \(a\) 进行尽可能少的操作,使得
\[\forall m,\sum_{i=1}^ma_i\geq \sum_{i=1}^m b_i \]一次操作形如:
- 选定正整数 \(i\),交换 \(a_i\) 和 \(a_{i+1}\)。
仅需求出最小操作次数。
解法:首先,使用极端法判断是否有解。
然后,考虑一次有效的操作能使得恰好一个前缀增加 \(2\),所以答案为
\[\frac{1}{2}\sum_{m=1}^n\max\{0,\sum_{i=1}^mb_i-\sum_{i=1}^ma_i\} \]使用前缀和算法可以 \(O(n)\) 完成。
【E】摸爬滚打
模拟赛题。一道广义容斥题。
首先,有一种暴力算法,枚举每一条路劲 \(\text{path}\in P\),其长度为 \(\text{len}\),则答案 \(\text{ans}\) 为:
\[\text{ans}=\frac{1}{|P|\binom{m}{k}}\sum_{\text{path}}\binom{m-\text{len}}{k} \]难以利用 \(k\) 较小的性质。
考虑广义容斥,钦定路径中有 \(i\) 条损坏,则有
\[\text{ans}=\frac{1}{|P|\binom{m}{k}}\sum_{i=0}^k(-1)^i\binom{m-i}{k-i}\sum_{\text{path}}\binom{\text{len}}{i} \]而 \(\displaystyle \sum_{\text{path}}\binom{\text{len}}{i}\) 为 \(\displaystyle [x^i]\sum_{\text{path}}(x+1)^{\text{len}}\),可以背包 dp 计算。
复杂度 \(O(nk)\)。
随机 dag 期望路径条数
据说是
\[\exp(\frac{m}{n}) \](其中 \(n\) 为点数,\(m\) 为边数)
不知道对不对。反正不多。
本题就放过了 \(O(\) 路劲数 \(\times \operatorname{poly}(n,m,k))\) 的做法。
多项式方法求组合数
因为 \(\displaystyle \binom{n}{i}\) 是 \([x^i](x+1)^n\),所以处理组合数可以使用背包 dp。
主要好处为,该式子可以接受一定程度的变形,如 \(\displaystyle \sum \binom{n}{i}\) 之类。
【E】Clues
结论板子题。
Submission #301605373 - Codeforces
一些有关树的结论
一些有关树的结论【随机树树高】【完全图生成树个数】【连接连通块方案数】【Prüfer 序列】【Prufer 序列】 - 洛谷专栏
【N】独脚大盗
模拟赛题目。prufer 序列相关的计数 + lagrange 插值。
设 \(f[n][m]\) 表示大小为 \(n\) 的图中,边权值域为 \([1,m]\) 的答案。然后,就能写出 \(O(n^3m)\) 的类似于多项式 exp 的 dp 转移。
然后,发现 \(f[n][m]\) 是关于 \(m\) 的多项式,于是,直接 lagrange 插值。
能做到 \(O(n^5)\)。
下面是一些公式
\[\begin{gathered} \left(\sum_i s_i\right)^{k-2}\prod_i s_i\\ f[n][m]=f[n][m-1]+\sum_{\sum_{i}s_i=n}n^{k-2}\prod_if[s_i][m-1]\binom{s_1+s_2+\cdots+s_i-1}{s_i-1}s_i(M-m+2)^{s_i(s_1+s_2+\cdots+s_{i-1})-1}\\ g_m[n][k]=\sum_{i=1}^{n-1}g_m[n-i][k-1]f[i][m-1]\binom{n-1}{i-1}i(M-m+2)^{i(n-i)-1}\\ g_m[n][1]=f[n][m-1]n\\ f[n][m]=f[n][m-1]+\sum_{k=2}^nn^{k-2}g_m[n][k] \end{gathered} \]lagrange 插值
lagrange 插值相关做题记录 - zhiyin123123 - 博客园
标签:洛谷,log,记录,text,复杂度,frac,dp From: https://www.cnblogs.com/zhiyin123/p/18680692