从DFT到FFT及其快速计算卷积上的代码实现,并搭建卷积神经网络
ps:原始代码来自https://www.ruanx.net/cheat-neural-network/。本文主要是在这个微型神经网络的基础上加点卷积成分。
傅里叶变换(Fourier Transform)是一种重要的数学工具,用于将时间域或空间域的信号转换到频域,揭示信号中的频率成分。它在信号处理、图像处理、通信系统、控制理论和其他许多领域中有着广泛的应用。
傅里叶变换的基本思想是将一个信号分解成正弦波和余弦波的叠加,每个波对应一个特定的频率。通过这种分解,可以将原始信号表示为这些频率成分的加权和,从而分析信号的频谱特性。
先给出傅里叶变换的公式:
傅里叶逆变换的公式:
中含有_ _,意味着要利用复平面来理解,同时,由于对t进行从无穷到无穷的积分,可以将视作一个顺时针转无数个圈的“欧拉转盘”。若f(t) = sin(3t),当且仅当w=3时,F(w) != 0;否则,由于能够转无数个圈,缠绕图像必定关于原点中心对称,最终导致积分为0;仅当w=3时,整个旋转图像呈现一个特殊的圆形,它的中心点不在原点。
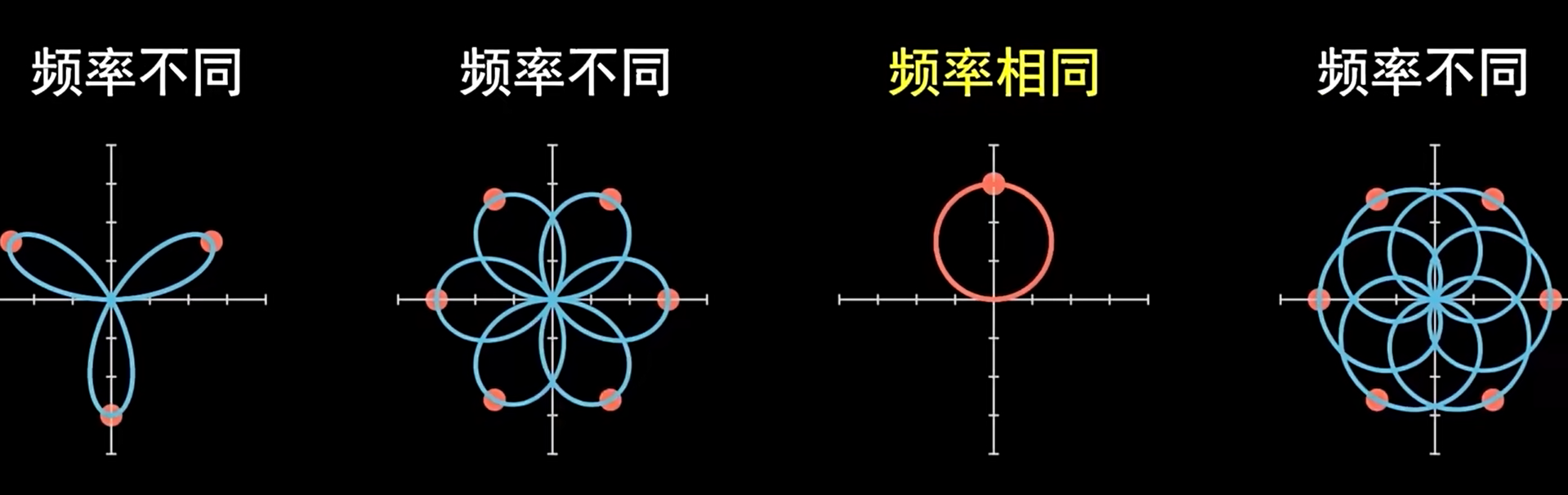
傅里叶变换将信号从时域转变为频域,从函数上来看,也就是将自变量 (时间)转为了自变量 (角速度,)。f(t)就是t时刻信号的振幅,获得的F(w)是整个信号在w对应频率下的振幅和相位。依靠复数的特性,F(w)的模长对应振幅,幅角对应相位。于是整个傅里叶变换的过程并没有产生信息的损失——它是可逆的。
而考虑实际应用,这个理论公式基本用不上。由于信号往往是通过采样获得的,因此离散条件下的傅里叶变换更为常用:
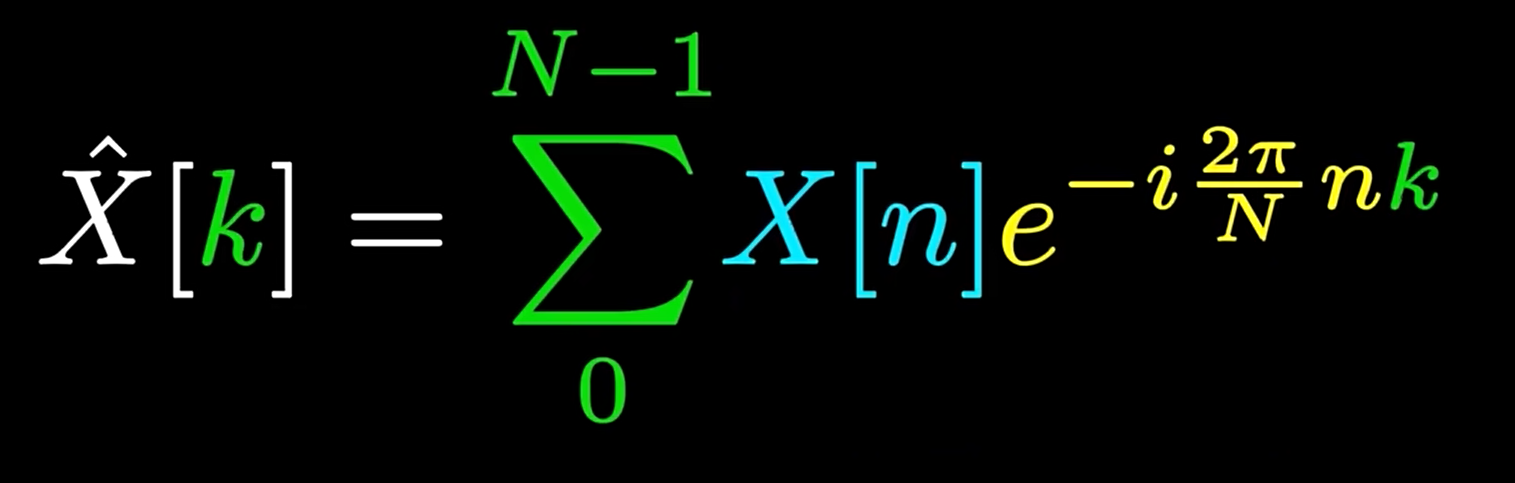
欧拉转盘并没有改变被分析的函数或矢量,而只是改变了旋转角。在公式中,k表示欧拉转盘的频率,黄色部分表示经过转盘调整后的旋转角。这样,我们将连续地旋转替换为了矢量内积:
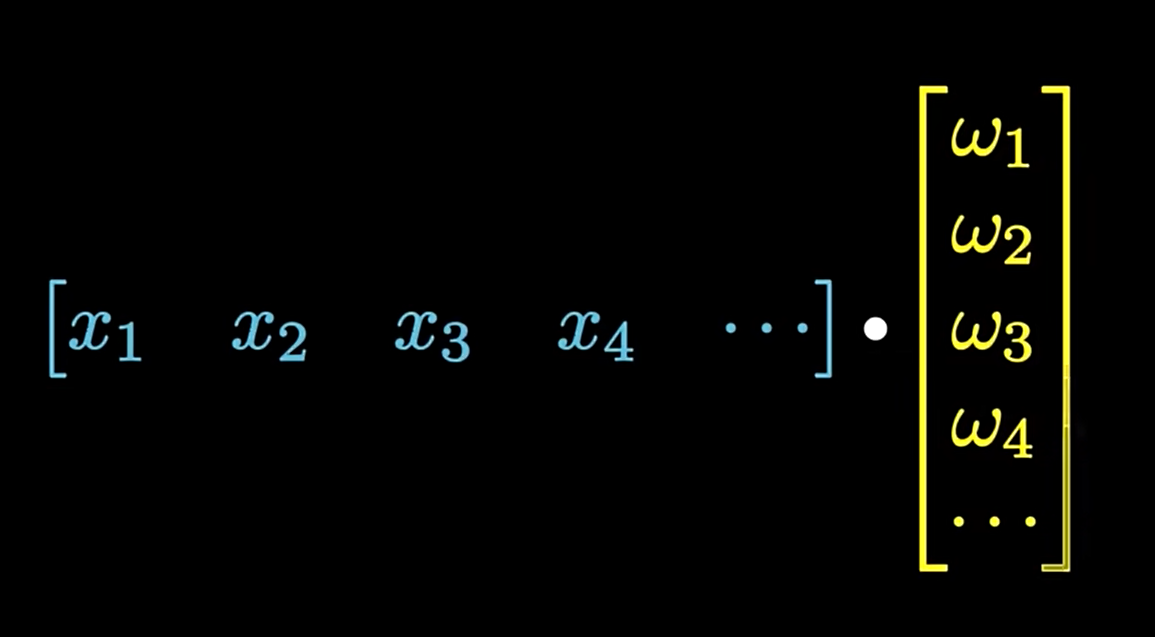
X[k]的长度一般设为与N相同。这个时候整个DFT可以视作一种矩阵乘法。
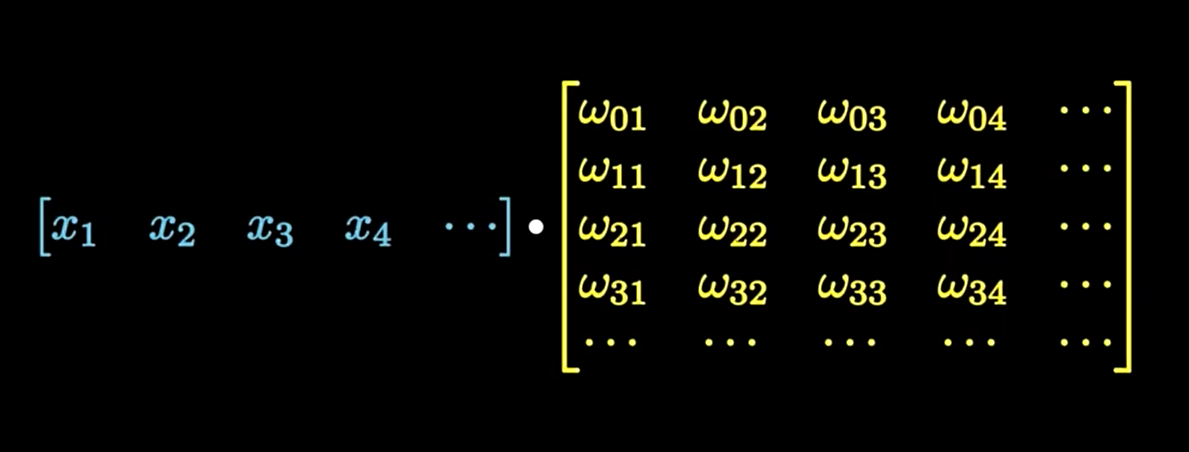
一般的傅里叶变换需要O(n^2)的时间复杂度,而快速傅里叶变换(FFT)将时间复杂度降为了O(nlogn)。下面先讲讲与FFT密切相关的:多项式相乘的优化算法。
考虑两个一般多项式的相乘,我们的乘法一般会花费O(n^2)的时间复杂度:用列表表示每一项的系数,然后进行离散上的卷积。
但事实上,一个多项式可以转变为一个偶函数和一个奇函数的和,已知n+1个点确定n次多项式,我们只需要知道(n+1)/2个点的值就可以利用奇偶性求解;而这个过程是可递归的,因此时间复杂度下降到了O(nlogn)。
FFT利用了与多项式乘法类似的分解和递归思想,用于高效计算DFT。具体来说,FFT算法通过将原始信号分解为奇数和偶数项,然后递归地计算频谱,最终合并结果。这一过程与多项式的递归分解非常相似,将输入信号 x[n]x[n] 分解为奇数项和偶数项:分别计算奇数项和偶数项的DFT(这里使用递归),合并奇数项和偶数项的DFT,得到最终的FFT结果,代码实现如下:
import numpy as np
def fft(x):
N = len(x)
if N <= 1:
return x
even = fft(x[0::2])
odd = fft(x[1::2])
T = [np.exp(-2j np.pi k / N) * odd[k] for k in range(N // 2)]
return [even[k] + T[k] for k in range(N // 2)] + [even[k] - T[k] for k in range(N // 2)]
# 示例输入
#x = np.random.random(8)
x = [1,2,3,4]
X = fft(x)
# 检查结果
print("输入信号: ", x)
print("FFT结果: ", X)
print("FFT模长: ", np.abs(X))
print("FFT幅角: ", np.angle(X))
输出如下:
我们理解了FFT,接下来讨论它在快速计算卷积上的利用。前面已经提到,多项式相乘可以用卷积进行计算,而类FFT的做法就将其进行了优化;我们引申出一个著名的定理:
频域卷积定理(Convolution Theorem)
频域卷积定理揭示了卷积和乘积之间的关系。具体地,它指出:
时域中的卷积对应于频域中的乘积。
时域中的乘积对应于频域中的卷积。
数学表达
设F(ω)和G(ω)分别是f(t)和g(t)的傅里叶变换,那么:
卷积定理:
F{f(t)∗g(t)}=F(ω)⋅G(ω)
乘积定理:
F{f(t)⋅g(t)}=1/2π(F(ω)∗G(ω))
其中,F表示傅里叶变换。
以下是证明过程:
证明卷积定理前,先对证明中用到的性质进行简单介绍。
傅立叶变换的时移性质。该性质表述为:设、为实常数,若,则
傅立叶变换的时移性质表明当一个信号沿时间轴平移后,各频率成份的大小不发生改变,但相位发生变化。该性质可以由傅立叶变换的定义进行证明:
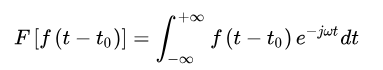
令,则有
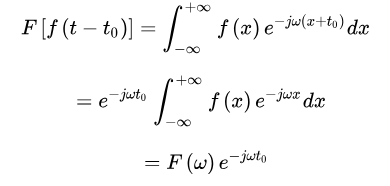
另外,由富比尼定理可知,积分区域连续的前提下,二重积分的积分次序可以交换。
下面对时域卷积定理和频域卷积定理进行推导证明。
时域定理证明
首先,卷积定义为
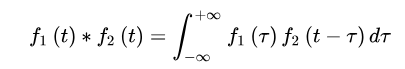
然后,代入傅立叶变换公式
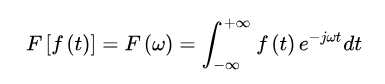
由此可得
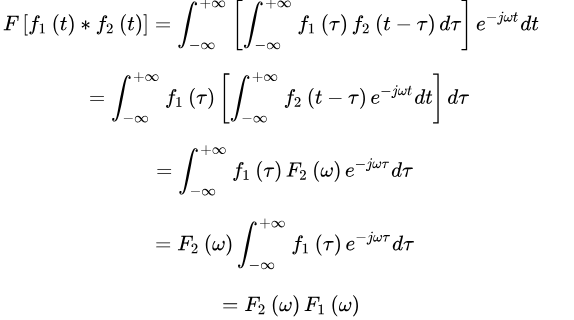
至此,时域卷积定理得证 [1]。
频域定理证明
设:
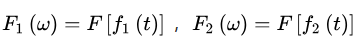
IF表示傅立叶逆变换,则
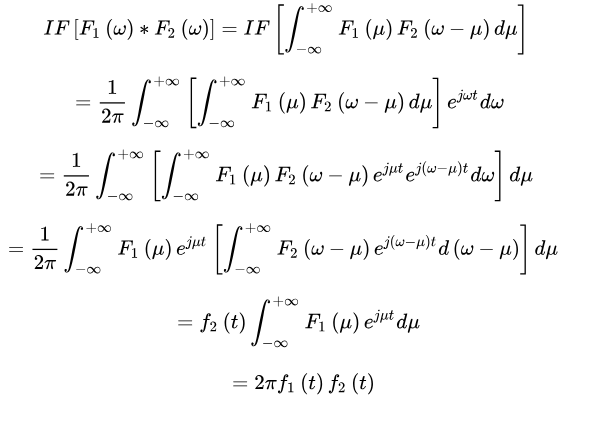
因此有
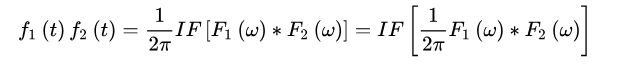
故频域卷积定理得证。
因此我们找到了一个快速计算卷积的方法,接下来我们用代码实现。
先定义一个IFFT函数:
def ifft(x):
N = len(x)
if N <= 1:
return x
even = ifft(x[0::2])
odd = ifft(x[1::2])
T = [np.exp(2j np.pi k / N) * odd[k] for k in range(N // 2)]
return [(even[k] + T[k]) / 2 for k in range(N // 2)] + [(even[k] - T[k]) / 2 for k in range(N // 2)]
再定义一个快速卷积函数:
def fft_convolution(signal1, signal2):
# 确定卷积结果的长度
n = len(signal1) + len(signal2) - 1
# 将信号零填充到相同长度的最小2的幂
N = 1
while N < n:
N *= 2
signal1_padded = np.pad(signal1, (0, N - len(signal1)), 'constant')
signal2_padded = np.pad(signal2, (0, N - len(signal2)), 'constant')
# 计算信号的FFT
fft_signal1 = fft(signal1_padded)
fft_signal2 = fft(signal2_padded)
# 在频域中相乘
fft_product = [a * b for a, b in zip(fft_signal1, fft_signal2)]
# 计算IFFT以获得卷积结果
convolution_result = ifft(fft_product)
# 截断零填充的部分
convolution_result = convolution_result[:n]
return convolution_result
测试数据:
# 示例输入
#x = np.random.random(8)
x = [1,2,3,4]
X = fft(x)
x2 = ifft(X)
# 检查结果
print("输入信号: ", x)
print("FFT结果: ", X)
print("FFT模长: ", np.abs(X))
print("FFT幅角: ", np.angle(X))
print("IFFT结果: ", np.abs(x2))
y1 = [1,2,3,4,5,6,7,8,9]
y2 = [9,8,7,6,5,4,3,2,1]
print(np.abs(fft_convolution(y1,y2)))
输出结果:
掌握了快速卷积算法的原理,我们就可以考虑将其运用在神经网络当中了。
MNIST数据集是一个经典的机器学习数据集,包含60,000张28x28像素的手写数字图片和10,000张测试图片,广泛用于图像分类任务和新手练习。
用pytorch写出一个简单的神经网络:
import sys
sys.path.append('/home/aistudio/external-libraries')
import torch
import torchvision
import torch.nn as nn
import torchvision.transforms as transforms
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
# 定义数据预处理步骤,将图像数据转换为PyTorch张量
trans_to_tensor = transforms.Compose([
transforms.ToTensor()
])
# 加载MNIST训练数据集
data_train = torchvision.datasets.MNIST(
'./mnist_data', # 数据存储路径
train=True, # 指定为训练数据集
transform=trans_to_tensor, # 应用预处理转换
download=True # 如果数据集不存在,则下载
)
# 加载MNIST测试数据集
data_test = torchvision.datasets.MNIST(
'./mnist_data', # 数据存储路径
train=False, # 指定为测试数据集
transform=trans_to_tensor, # 应用预处理转换
download=True # 如果数据集不存在,则下载
)
# 创建数据加载器,将训练数据分成批次,每批次包含100个样本,且每次迭代时打乱数据顺序
train_loader = torch.utils.data.DataLoader(
data_train,
batch_size=100,
shuffle=True
)
# 定义一个简单的神经网络类,继承自nn.Module
class MyNet(nn.Module):
# 初始化函数,定义网络的层次结构
def init(self):
super().init()
# 定义第一个全连接层,将输入的28x28的图像展平到100维
self.fc1 = nn.Linear(28*28, 100)
# 定义第二个全连接层,将100维的输入转换到10维的输出
self.fc2 = nn.Linear(100, 10)
# 前向传播函数,定义数据如何通过网络
def forward(self, x):
# 将输入x展平成1维向量(大小为28x28)
x = x.view(-1, 28*28)
# 通过第一个全连接层
x = self.fc1(x)
# 使用ReLU激活函数
x = F.relu(x)
# 通过第二个全连接层
x = self.fc2(x)
# 使用sigmoid激活函数
x = torch.sigmoid(x)
return x
# 创建网络实例
net = MyNet()
# 定义设备为CPU
device = torch.device('cpu')
# 将网络移动到设备上
net.to(device)
# 定义损失函数为交叉熵损失
criterion = nn.CrossEntropyLoss()
# 定义优化器为Adam,并传入网络的参数
optimizer = torch.optim.Adam(net.parameters())
# 定义测试函数,用于评估模型的性能
def test(net):
# 设置模型为评估模式
net.eval()
# 创建测试数据加载器,不打乱数据,批次大小为10000
test_loader = torch.utils.data.DataLoader(data_train, batch_size=10000, shuffle=False)
test_data = next(iter(test_loader))
# 禁用梯度计算
with torch.no_grad():
x, y = test_data[0].to(device), test_data[1].to(device)
# 前向传播,得到模型输出
outputs = net(x)
# 获取预测结果
pred = torch.max(outputs, 1)[1]
# 打印测试准确率
print(f'test acc: {sum(pred == y) / outputs.shape[0]}')
# 恢复模型为训练模式
net.train()
# 定义训练函数,用于训练模型
def fit(net, epoch=1):
# 设置模型为训练模式
net.train()
run_loss = 0
# 迭代每个训练周期
for num_epoch in range(epoch):
print(f'epoch {num_epoch}')
# 迭代每个数据批次
for i, data in enumerate(train_loader):
x, y = data[0].to(device), data[1].to(device)
# 前向传播,得到模型输出
outputs = net(x)
# 计算损失
loss = criterion(outputs, y)
# 清零梯度
optimizer.zero_grad()
# 反向传播
loss.backward()
# 更新参数
optimizer.step()
# 累计运行损失
run_loss += loss.item()
# 每100个批次打印一次损失并进行测试
if i % 100 == 99:
print(f'[{i+1} / 600] loss={run_loss / 100}')
run_loss = 0
test(net)
# 运行训练函数,设置训练周期为5
fit(net, epoch=5)
最终测试结果为:
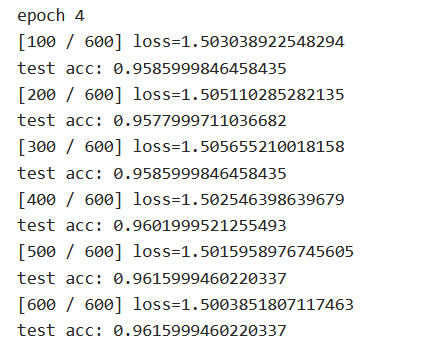
准确率达到了96.159%。接下来我们将其改造为卷积神经网络,看看经过卷积后,它的准确率能否被提高。
卷积神经网络(Convolutional Neural Networks, CNN)这个概念的提出可以追溯到二十世纪80~90年代,但是有那么一段时间这个概念被“雪藏”了,因为当时的硬件和软件技术比较落后,而随着各种深度学习理论相继被提出以及数值计算设备的高速发展,卷积神经网络得到了快速发展。整个过程需要在如下几层进行运算:
输入层:输入图像等信息
卷积层:用来提取图像的底层特征
池化层:防止过拟合,将数据维度减小
全连接层:汇总卷积层和池化层得到的图像的底层特征和信息
输出层:根据全连接层的信息得到概率最大的结果
输入层比较简单,这一层的主要工作就是输入图像等信息,因为卷积神经网络主要处理的是图像相关的内容,但是我们人眼看到的图像和计算机处理的图像是一样的么?很明显是不一样的,对于输入图像,首先要将其转换为对应的二维矩阵,这个二位矩阵就是由图像每一个像素的像素值大小组成的。这这样的图像被称为灰度图像,因为其每一个像素值的范围是0255(由纯黑色到纯白色),表示其颜色强弱程度。另外还有黑白图像,每个像素值要么是0(表示纯黑色),要么是255(表示纯白色)。我们日常生活中最常见的就是RGB图像,有三个通道,分别是红色、绿色、蓝色。每个通道的每个像素值的范围也是0255,表示其每个像素的颜色强弱。但是我们日常处理的基本都是灰度图像,因为比较好操作(值范围较小,颜色较单一),有些RGB图像在输入给神经网络之前也被转化为灰度图像,也是为了方便计算,否则三个通道的像素一起处理计算量非常大。当然,随着计算机性能的高速发展,现在有些神经网络也可以处理三通道的RGB图像。现在我们已经知道了,输入层的作用就是将图像转换为其对应的由像素值构成的二维矩阵,并将此二维矩阵存储,等待后面几层的操作。
那图片输入进来之后该怎么处理呢?假设我们已经得到图片的二维矩阵了,想要提取其中特征,那么卷积操作就会为存在特征的区域确定一个高值,否则确定一个低值。这个过程需要通过计算其与卷积核(Convolution Kernel)的乘积值来确定。假设我们现在的输入图片是一个人的脑袋,而人的眼睛是我们需要提取的特征,那么我们就将人的眼睛作为卷积核,通过在人的脑袋的图片上移动来确定哪里是眼睛。
通过整个卷积过程又得到一个新的二维矩阵,此二维矩阵也被称为特征图(Feature Map),最后我们可以将得到的特征图进行上色处理(我只是打个比方,比如高值为白色,低值为黑色),最后可以提取到关于人的眼睛的特征。
首先卷积核也是一个二维矩阵,当然这个二维矩阵要比输入图像的二维矩阵要小或相等,卷积核通过在输入图像的二维矩阵上不停的移动,每一次移动都进行一次乘积的求和,作为此位置的值。
可以看到,整个过程就是一个降维的过程,通过卷积核的不停移动计算,可以提取图像中最有用的特征。我们通常将卷积核计算得到的新的二维矩阵称为特征图,比如上方动图中,下方移动的深蓝色正方形就是卷积核,上方不动的青色正方形就是特征图。
注意到,每次卷积核移动的时候中间位置都被计算了,而输入图像二维矩阵的边缘却只计算了一次,会不会导致计算的结果不准确呢?
让我们仔细思考,如果每次计算的时候,边缘只被计算一次,而中间被多次计算,那么得到的特征图也会丢失边缘特征,最终会导致特征提取不准确,那为了解决这个问题,我们可以在原始的输入图像的二维矩阵周围再拓展一圈或者几圈,这样每个位置都可以被公平的计算到了,也就不会丢失任何特征,此过程可见下面两种情况,这种通过拓展解决特征丢失的方法又被称为Padding。
那如果情况再复杂一些呢?如果我们使用两个卷积核去提取一张彩色图片呢?之前我们介绍过,彩色图片都是三个通道,也就是说一个彩色图片会有三个二维矩阵,当然,我们仅以第一个通道示例,否则太多了也不好介绍。此时我们使用两组卷积核,每组卷积核都用来提取自己通道的二维矩阵的特征,刚才说了,我们只考虑第一通道的,所以说我们只需要用两组卷积核的第一个卷积核来计算得到特征图就可以了。
刚才我们也提到了,有几个卷积核就有多少个特征图,现实中情况肯定更为复杂,也就会有更多的卷积核,那么就会有更多的特征图,当特征图非常多的时候,意味着我们得到的特征也非常多,但是这么多特征都是我们所需要的么?显然不是,其实有很多特征我们是不需要的,而这些多余的特征通常会给我们带来如下两个问题:
过拟合
维度过高
为了解决这个问题,我们可以利用池化层,那什么是池化层呢?池化层又称为下采样,也就是说,当我们进行卷积操作后,再将得到的特征图进行特征提取,将其中最具有代表性的特征提取出来,可以起到减小过拟合和降低维度的作用。
理论到此结束,我们开始实践。
Pytorch很方便地为我们准备了.Conv2d函数来进行卷积操作。
def init(self):
super().init()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=16, kernel_size=5, stride=1, padding=0) # 卷积层:输入通道1,输出通道16,卷积核大小5x5
self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2) # 最大池化层,核大小为2,步幅为2,将图像大小变为原来的1/4(1/2*1/2 = 1/4)
self.conv2 = nn.Conv2d(in_channels=16, out_channels=36, kernel_size=3, stride=1, padding=0) # 卷积层2:输入通道16,输出通道32,卷积核大小3x3
self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2) # 最大池化层2
# 定义第一个全连接层,将输入的36x5x5的图像展平到100维
self.fc1 = nn.Linear(3655, 100)
# 定义第二个全连接层,将100维的输入转换到10维的输出
self.fc2 = nn.Linear(100, 10)
def forward(self, x):
# 卷积层1 -> 激活函数(relu) -> 池化层1
x = self.pool1(F.relu(self.conv1(x)))
x = self.pool2(F.relu(self.conv2(x)))
# 将输入x展平成1维向量,大小为36x5x5
x = x.view(-1, 3655)
# 通过第一个全连接层
x = self.fc1(x)
# 使用ReLU激活函数
x = F.relu(x)
# 通过第二个全连接层
x = self.fc2(x)
# 使用sigmoid激活函数
x = torch.sigmoid(x)
return x
# 使用sigmoid激活函数
x = torch.sigmoid(x)
return x

使用卷积神经网络,准确率显著提升到了98.580%。
至此,我们成功将积分变换中的卷积应用在神经网络的搭建上,并显著提高了它的识别能力。
标签:入门,卷积,self,FFT,神经网络,图像,np,输入 From: https://www.cnblogs.com/tomorin/p/18680227