神经网络的误差反向传播,初次接触的时候,感觉思路并不复杂,但其中包含许多细节,容易产生迷惑。今天整理一下思路,仅供参考。
一、神经网络的定义

最常见的神经网络长这个样子,包含一个输入层、若干隐藏层和一个输出层。
输入向量:
第层的权重矩阵:
第层的偏置向量:
第层的输出:
神经网络整体的表达式:
其中,为第
层的激活函数。这里注意激活函数的几个主要作用:一是增加层与层之间的非线性因素,防止神经网络退化;二是将层运算的结果映射到理想的结果空间,以起到激活或过滤的作用;三是采用合理的激活函数,能够简化误差反向传播的计算。
上述便是神经网络基本定义的所有要素了。
二、训练神经网络
1、训练神经网络是在干什么
我们训练神经网络这个举动,是利用输入空间中的部分输入
和对应的真实结果
,来对一组预设的权重
和偏置
参数进行优化的过程。经过优化之后的参数,能够准确地揭示输入与输出之间的内在关系,我们称之为模型。利用训练好的模型,我们能够关联输入空间任意输入与输出。
2、目标函数(损失函数)
目标函数(损失函数)是神经网络输出与真实值(标签)
的均方差之和:
是一组输入
在预设参数下的输出,而
则是真实结果。要想使
运算结果更接近真实结果
,也就是求
的最小值。
神经网络训练的过程,就是对目标函数(损失函数)最优化。由于最优化的过程并不是一个计算准确结果的过程,因此可以对函数进行适当的变形以实现简化计算的目的(这里利用的是求方差)。
3、梯度下降法
对目标函数(损失函数)最优化,需要对所有的参数进行调整,具体到某一个参数,例如
或
,则是求
或
对
函数的偏导数,利用梯度下降法,逐步找到能够使
取到最小值的那个
或
。
4、引入德尔塔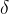
由于神经网络的维度和层数增加以及非线性激活函数等因素,直接求或
对
函数的偏导数,十分困难。
本身是一个非线性复合函数,利用复合函数的链式求导法则,可以把参数
或
对
求偏微分的过程,分割成易于求解的部分,再加上合适的激活函数,可以大大简化偏微分求解过程。
就是在这样的情况下引入的一个中间结果:
其中表示某一层
和
的加权输入,
表示输入函数对输出函数的偏导(变化量),也被称为“误差”(更详细的解释请参考神经网络的德尔塔(Delta)到底是什么)。凭借
在不同层的可推导性和可复用性,以及激活函数简化计算的加持,先求出输出层的
和
、
对
的偏微分,然后向前反推,就可以逐层求得
、
对
的偏微分结果,并逐层对
、
进行更新优化了。
三、总结
训练神经网络的主要思路,就是对预设参数的目标函数进行最优化,优化参数是通过梯度下降法求参数对函数的偏导数实现的,为了简化计算过程,其中引入了这样一个中间值(误差),通过反向传播的方式逐步求得每一层得参数,并进行优化。