介绍
2022 年,在科罗拉多州博览会艺术大赛上,一件开创性的作品打破了艺术创作的传统界限。杰森·M·艾伦的杰作《空间歌剧剧院》赢得了一等奖,打破了传统。它不是通过传统方式,而是使用扩散模型来生成图像。通过将文本提示变成超现实的图像,艾伦的创作不仅吸引了观众和评委,还引发了艺术家的强烈反对,他们指责他本质上是在作弊。

科罗拉多州博览会的“Théâtre D'opéra Spatial”参赛作品。
突破了之前由生成对抗网络 (GAN) 统治的图像合成的界限。事实上,据说扩散模型在图像合成方面胜过 GAN 。
在本文中,将探索扩散模型的理论基础,揭示其内部工作原理,了解其基本组成部分和显著的有效性。在此过程中,将重点介绍最受欢迎的扩散模型系列之一:稳定扩散。
揭开扩散模型成功背后的秘密,以及它们如何彻底改变图像生成。到最后,您将深刻理解它们的变革潜力,激发人工智能驱动的创造力。
扩散模型 Diffusion Models
扩散模型是一种生成模型,它在训练过程中从数据中学习,并根据所学内容生成类似的示例。这些模型从非平衡热力学中汲取灵感,在生成各种形式的数据方面取得了最先进的质量。一些示例包括生成高质量图像甚至音频(例如音频扩散模型 )。
简而言之,扩散模型的工作原理是通过添加高斯噪声来破坏训练数据(称为正向扩散过程),然后学习如何通过逐步逆转此噪声过程来恢复原始信息(称为反向扩散过程)。一旦训练完成,这些模型就可以通过采样随机高斯噪声并将其传递给学习到的去噪过程来生成新数据。
扩散模型不仅仅是创建高质量的图像。它们通过解决与 GAN 中的对抗性训练相关的众所周知的挑战而广受欢迎。扩散模型在训练稳定性、效率、可扩展性和并行化方面具有优势。
在以下章节中,将深入探讨扩散模型的细节。将探索正向扩散过程、反向扩散过程,并概述训练过程中涉及的步骤。此外,还将直观地了解损失函数的计算。通过研究这些组件,将全面了解扩散模型如何运作以及它们如何实现令人印象深刻的结果。
正向扩散过程
正向扩散过程包括逐步向输入图像添加高斯噪声,总共T步。在步骤 0 时,得到原始图像,在步骤 1 时,图像损坏程度非常轻微,并且会逐步进一步损坏,直到原始图像的全部信息都丢失。
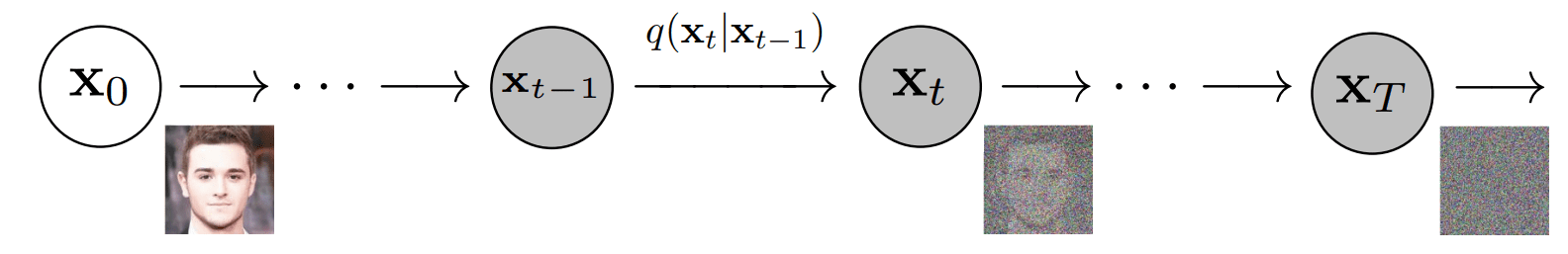
为了形式化这个过程,可以将其视为具有 T 步骤的固定马尔可夫链,其中时间步骤t处的图像映射到时间步骤t+1处的后续状态。因此,每个步骤仅取决于前一个步骤,这使能够推导出一个闭式公式来获取任何所需时间步骤的损坏图像,而无需进行迭代计算。
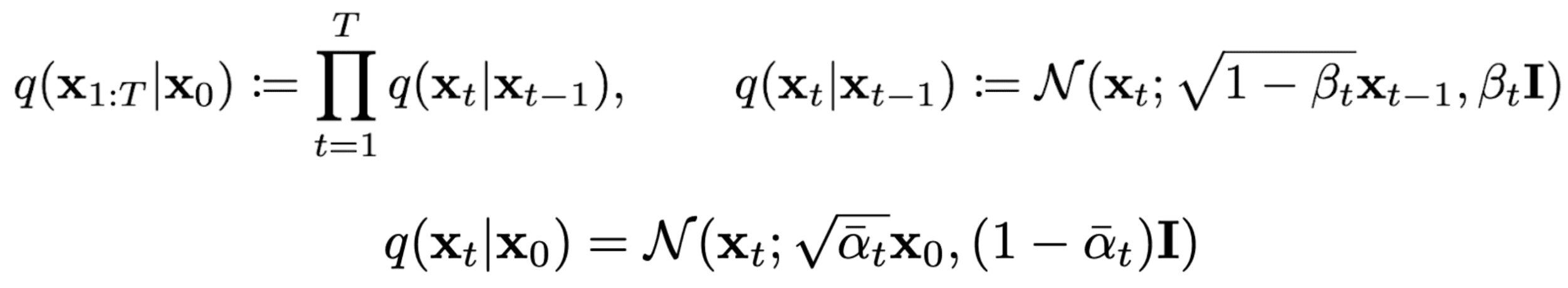
因此,该闭式公式能够在任意时间步直接采样 xₜ,从而显著加速前向扩散过程。
调度器Schedulers
此外,每一步的噪声添加都遵循一个精心设计的模式。调度程序确定要添加的噪声量。在原始的去噪扩散概率模型 (DDPM) 论文 中,作者定义了一个线性调度,范围为βₜ从时间步 0 的 0.0001 到时间步 T 的 0.02。然而,一些替代方案越来越受欢迎,例如在改进的去噪扩散概率模型论文中引入的余弦调度。
例如,下图显示了前向扩散过程中使用线性计划和余弦计划之间的差异。第一行显示线性计划,而第二行显示改进的余弦计划。

线性和余弦调度器,摘自《Improved DDPM》论文[5]
改进的 DDPM 论文的作者认为余弦调度提供了优越的性能。线性调度可能会导致输入图像中的信息快速丢失。因此,这通常会导致突然的扩散过程。相比之下,余弦调度提供了更平滑的退化。因此,允许后续步骤对没有被噪声完全淹没的图像进行操作。
逆扩散
与正向扩散过程相反,反向扩散过程带来了计算挑战,因为 q(xₜ₋₁|xₜ) 的公式变得难以处理或无法计算。为了应对反向扩散过程的挑战,深度学习模型成为人们关注的焦点,使用神经网络来近似这种难以捉摸的反向扩散过程。
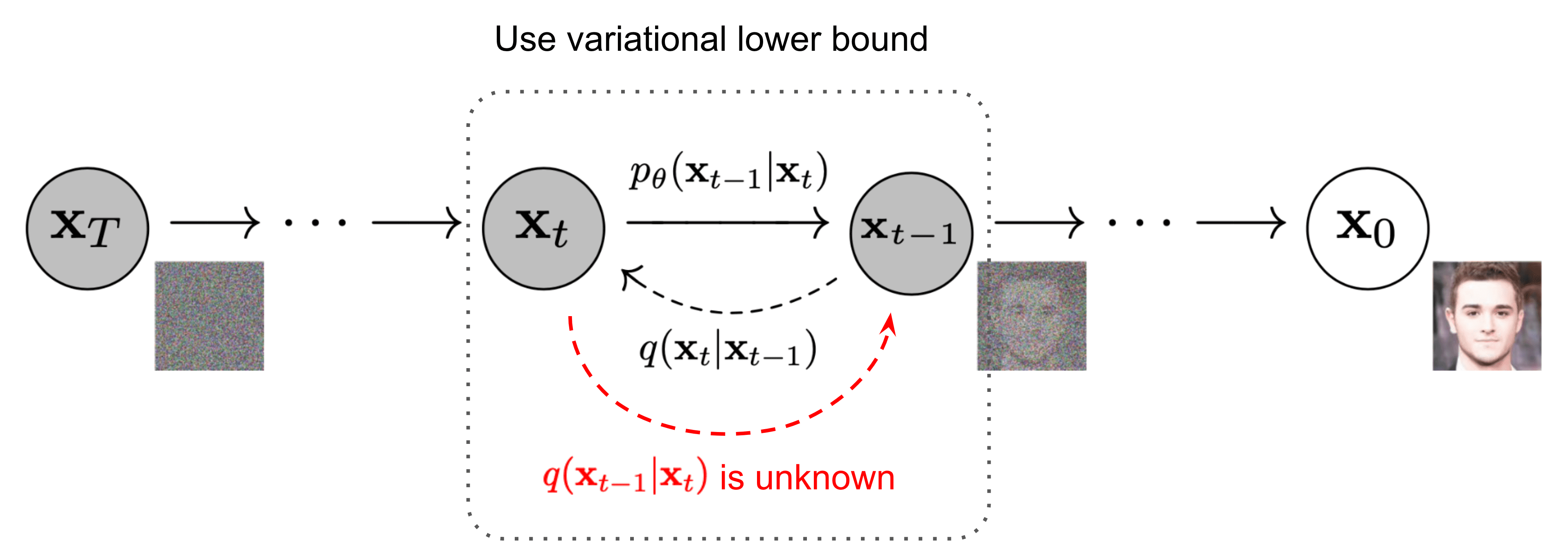
一般来说,该神经网络的作用是预测在某个时间步长t 时图像中存在的全部噪声。然后,通过将此预测与添加到图像中的实际噪声进行比较,可以训练网络。在推理时,这些网络仍然预测在时间步长 t 时图像中存在的全部噪声,然后根据所使用的调度程序仅去除一小部分噪声。
因此,通过预测时间步长t 的噪声,可能会试图仅用一步就检索到原始图像。然而,一些经验实验表明,需要更小的步骤来实现更高的稳定性。因此,只需去除时间步长t处图像中存在的一小部分噪声即可获得时间步长t-1 处的图像。
一些论文和博客可能会产生误导,因为人们在阅读这些论文和博客时,往往会认为网络可以预测从时间步t-1到时间步t 增加的噪声。不过,这可以通过查看作者提供的代码来澄清。
神经网络架构
您可能想知道这个神经网络的架构。一般来说,扩散模型使用某种 U-Net 变体来近似反向扩散过程。这种选择源于 U-Net 在计算机视觉社区中的流行。此外,考虑到唯一的要求是扩散模型的输入和输出必须保持相同的维度,这似乎很合适,超分辨率扩散模型除外。
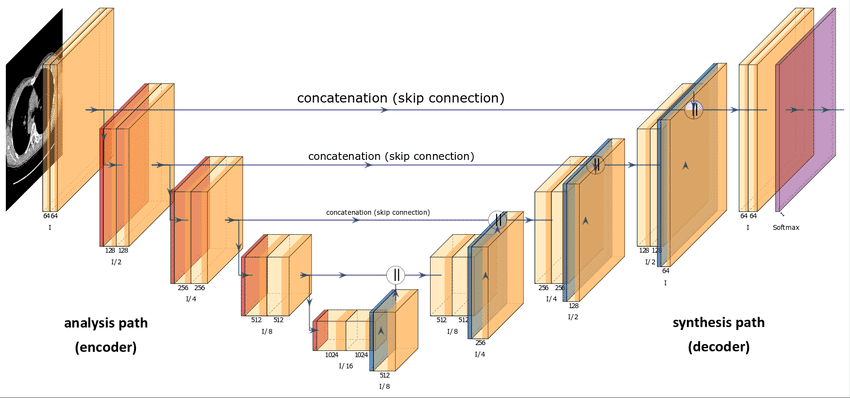
关于 DDPM 论文中概述的实施细节,主要的架构选择涉及:
- 编码器和解码器路径具有相同数量的级别,它们之间包含一个瓶颈块。
- 除最后一级外,每个编码器阶段均由两个具有卷积下采样的残差块组成。
- 每个解码器阶段由三个残差块组成。此外,作者还定义了 x2 近邻上采样块,并使用卷积来恢复来自上一级的输入。
- 解码器路径通过跳过连接与编码器路径中的各个阶段相连。
- 在模型中的单个特征图分辨率上使用注意力模块。
- 此外,时间步长 t被编码到时间嵌入中。这与Transformer 论文 [9]中提出的正弦位置编码非常相似。
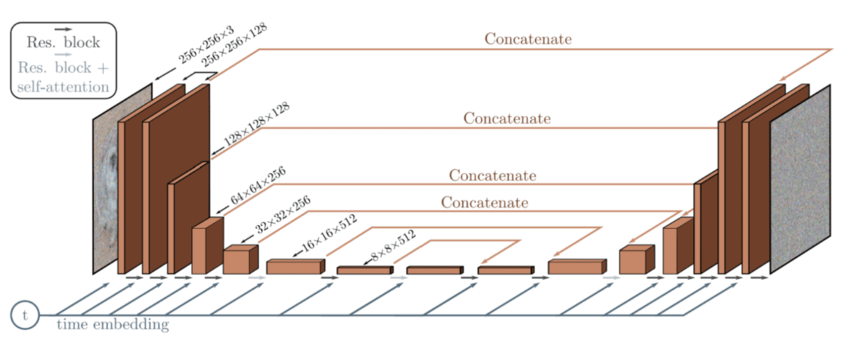
这些时间嵌入有助于神经网络获取图像当前处于哪个状态(步骤)的某些信息。这有助于了解图像中当前是否存在更多或更少的噪声,从而使模型减去更多或更少的噪声。一般而言,在较低的时间步长中,前向扩散过程增加的噪声比在较高的时间步长中少。
举个例子,整个正向/反向扩散过程如下:
损失计算
要训练扩散模型,目标是找到最大化训练数据似然性的反向马尔可夫转换。这相当于最小化负对数似然性的变分下限 (VLB)。虽然它被称为下限,但从技术上讲,它是一个上限,即证据下限 (ELBO) 的负数。但是,坚持参考文献,以保证不同来源之间的一致性。在实践中,最大化似然性转化为最小化负对数似然性
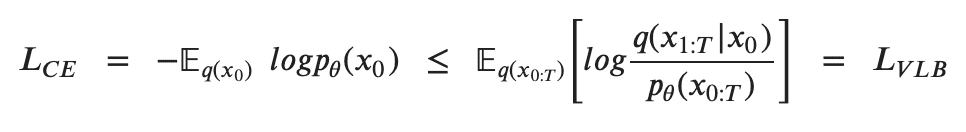
为了将方程中的每个项转换为可分析计算的,可以进一步将目标重写为几个KL 散度和熵项的组合。
使用 KL 散度进行重新表述
KL 散度测量概率分布之间的不对称统计距离,量化一个分布P与参考分布Q 的差异程度。用 KL 散度来表示VLB是可取的,因为马尔可夫链中的过渡分布是高斯分布,而高斯分布之间的 KL 散度具有封闭形式。
连续分布的 KL 散度的数学表示为:
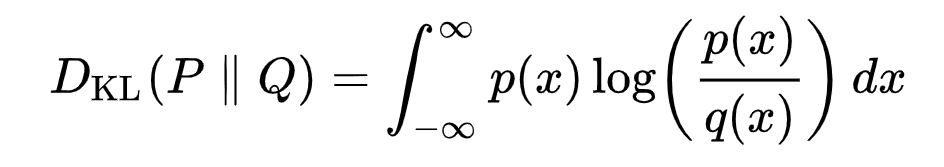
但这在实践中是什么样子的?提供了一个示例图,说明了变化分布P (蓝色分布)与参考分布Q (红色分布)的 KL 散度。绿色曲线表示 KL 散度定义中的积分内的函数,曲线下的总面积表示特定时刻P与Q的 KL 散度值,以数字形式显示。
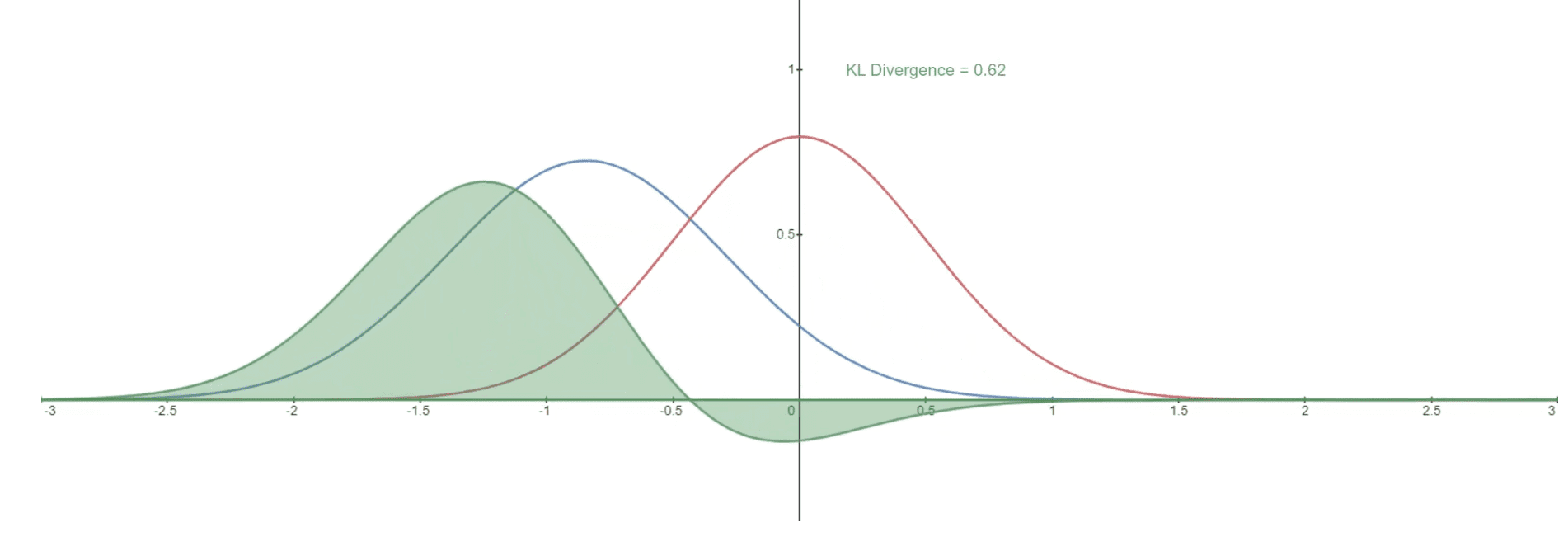
两个给定分布的 KL 散度表示:Q(参考分布)和 P(变化分布)
KL 散度比较了扩散训练管道中的高斯分布:添加了高斯噪声的前向扩散的参考分布,以及反向扩散期间的预测噪声。
不会深入研究扩散模型的数学。尽管如此,希望这有助于概述这些模型如何计算损失并更新其参数。该模型使用固定标准差和前向扩散的实际平均值以及添加噪声的平均值和标准差来预测特定时间步长t 的噪声。计算这些分布上图像的 KL 散度。此计算涵盖所有批次图像,从而促进神经网络反向传播。
训练过程
在每个批次的训练过程中,采取以下步骤:
- 对批次内的每个训练样本(例如图像)进行随机时间步长 t采样
- 根据时间步长t,使用闭式公式添加高斯噪声
- 将时间步长转换为嵌入,以提供给 U-Net 或类似模型(或其他模型系列)
- 使用带有噪声和时间嵌入的图像作为输入来预测图像中存在的噪声
- 将预测噪声与实际噪声进行比较,计算损失函数
- 使用损失函数通过反向传播更新扩散模型参数
这个过程在每个时期重复,使用相同的图像。然而,通常在不同的时期对每幅图像采样不同的时间步长。这使得模型能够在任何时间步长学习逆转扩散过程,从而增强其适应性

采样过程
对于采样新图像,不同之处在于没有输入图像。采样随机高斯噪声并定义生成新图像需要多少噪声步骤(T)。在每个步骤中,扩散模型预测图像中存在的全部噪声,将当前时间步长作为输入。然后,它仅去除该预测噪声的一小部分。经过 T 推理步骤后,获得图像生成结果。
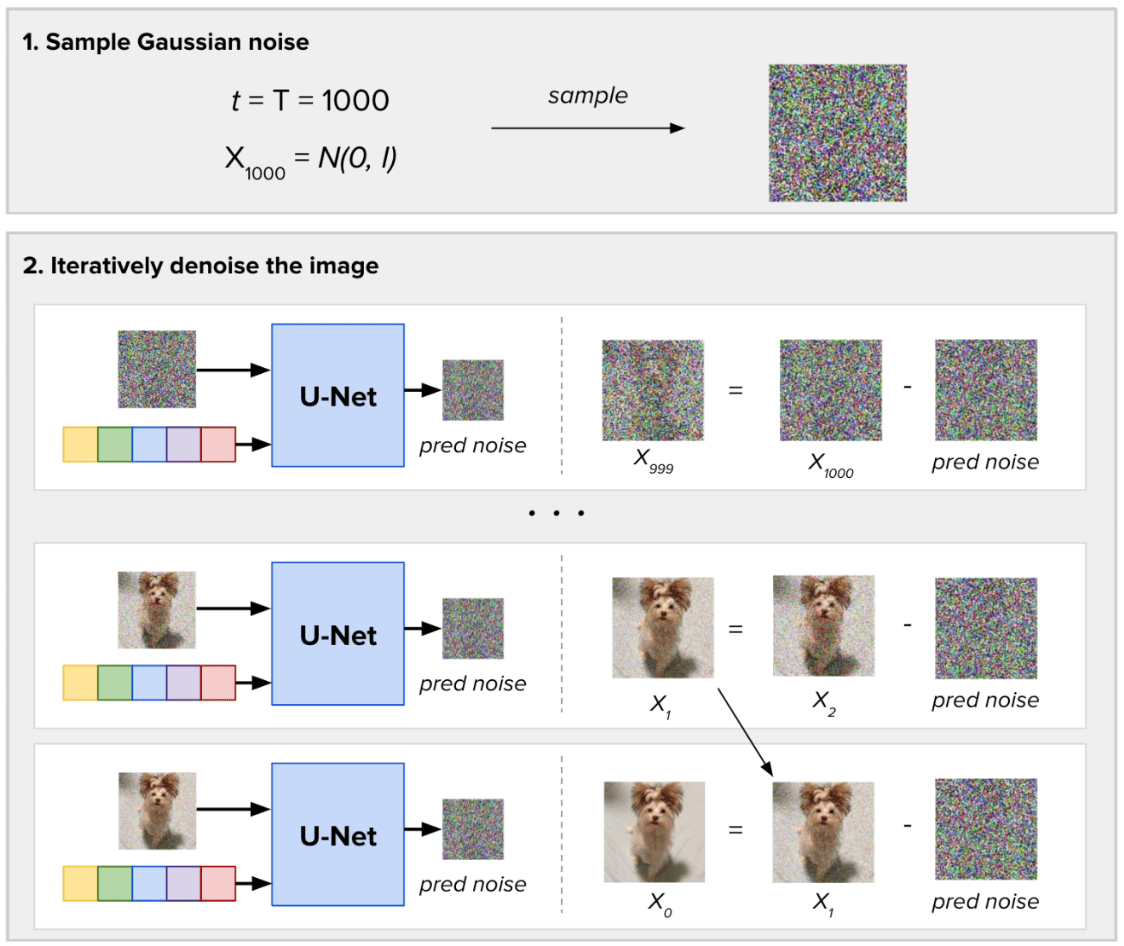
单幅图像的去噪过程
稳定扩散
传统扩散模型中的反向扩散过程涉及将全尺寸图像迭代地通过 U-Net 架构,以获得最终的去噪结果。然而,这种迭代性质在计算效率方面带来了挑战。在处理大图像尺寸和大量扩散步骤 (T) 时,这一点尤为突出。在采样过程中对图像进行高斯噪声去噪所需的时间可能会变得非常长。为了解决这个问题,一组研究人员提出了一种称为稳定扩散的新方法,最初称为潜在扩散模型 (LDM Latent Diffusion Model ) 。
将探讨本文提出的扩散模型的主要进展:处理潜在空间中的图像和条件反射。
潜在Latent 扩散模型
稳定扩散通过在潜在空间中执行扩散过程引入了一个关键的修改。其工作原理是使用经过训练的编码器E将全尺寸图像编码为较低维度表示(潜在空间)。然后在潜在空间内进行正向扩散过程和反向扩散过程。之后,使用经过训练的解码器D ,可以将图像从其潜在表示解码回像素空间。为了构建编码器和解码器,可以训练 变分自动编码器 (VAE)的一些变体。然后解耦该网络以分别使用两个组件。
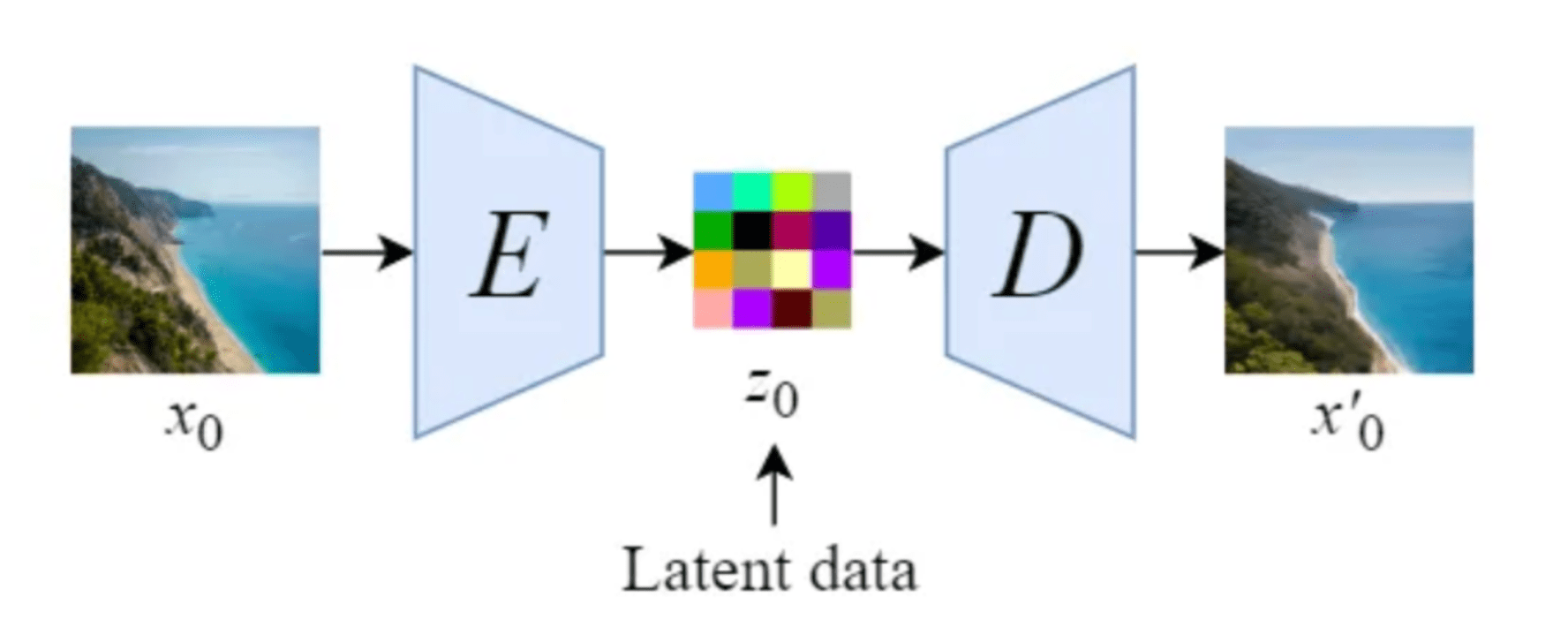
稳定扩散论文中提出的自动编码器图示
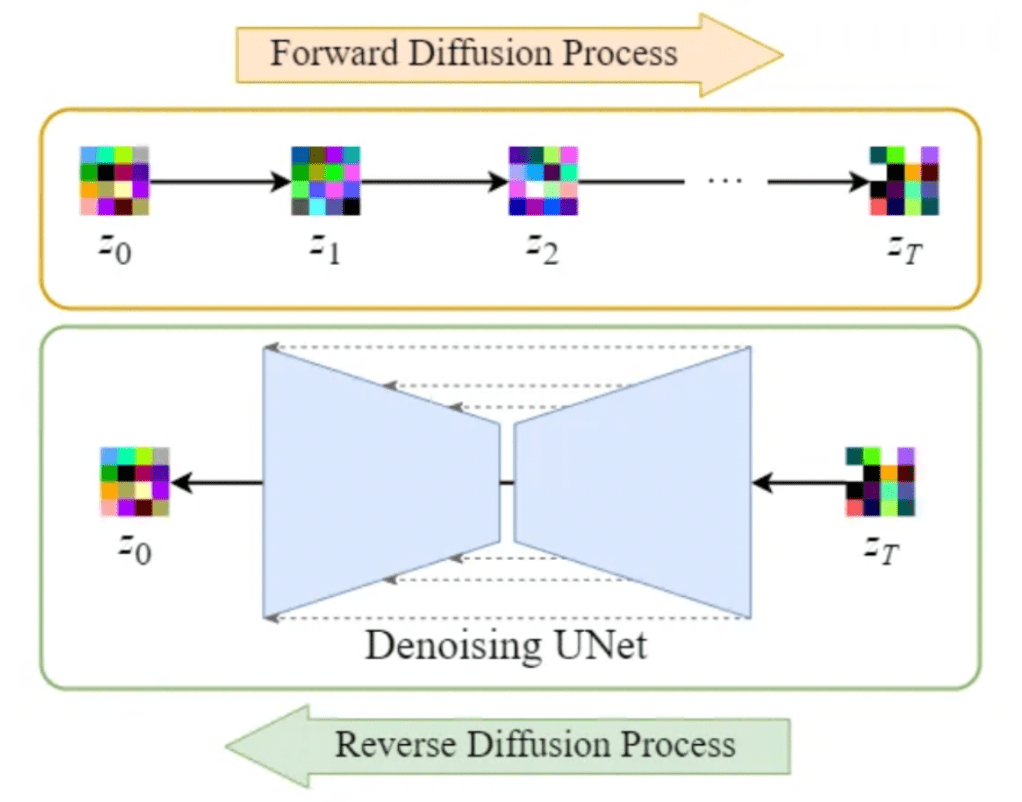
在稳定扩散中将扩散操作转移到潜在空间可提高速度并降低成本。这一进步加速了去噪和采样过程,使其成为高质量图像生成和稳定训练的有效解决方案。
通过利用潜在空间,稳定扩散减轻了反向扩散过程中的计算负担。这可以更快地对图像进行去噪,从而提高速度以及整体模型的稳定性和稳健性。
调节Conditioning
在此之前,生成特定类别的图像主要通过在输入中添加类别标签来实现。通常称为分类器指导。然而,稳定扩散模型的突出特点之一是它能够根据特定的文本提示或其他条件输入生成图像。这是通过在内部扩散模型中引入条件机制来实现的,在文献中也称为无分类器指导 (CFG Classifier-Free Guidance) 。
为了实现调节生成,内部扩散模型的去噪 U-Net 采用了交叉注意机制。这使得模型能够在图像生成(去噪)过程中有效地整合条件反射信息。
根据所需的输出,条件输入可以采用多种形式:
- 文本输入首先通过 BERT 或 CLIP 等语言模型转换为嵌入。在条件反射中,使用多头注意力层将这些嵌入映射到 U-Net 中,在图中表示为 Q、K 和 V。
- 其他条件输入(如语义图、图像或修复等空间对齐数据)的作用类似。然而,这些条件机制的整合通常是通过串联来实现的。
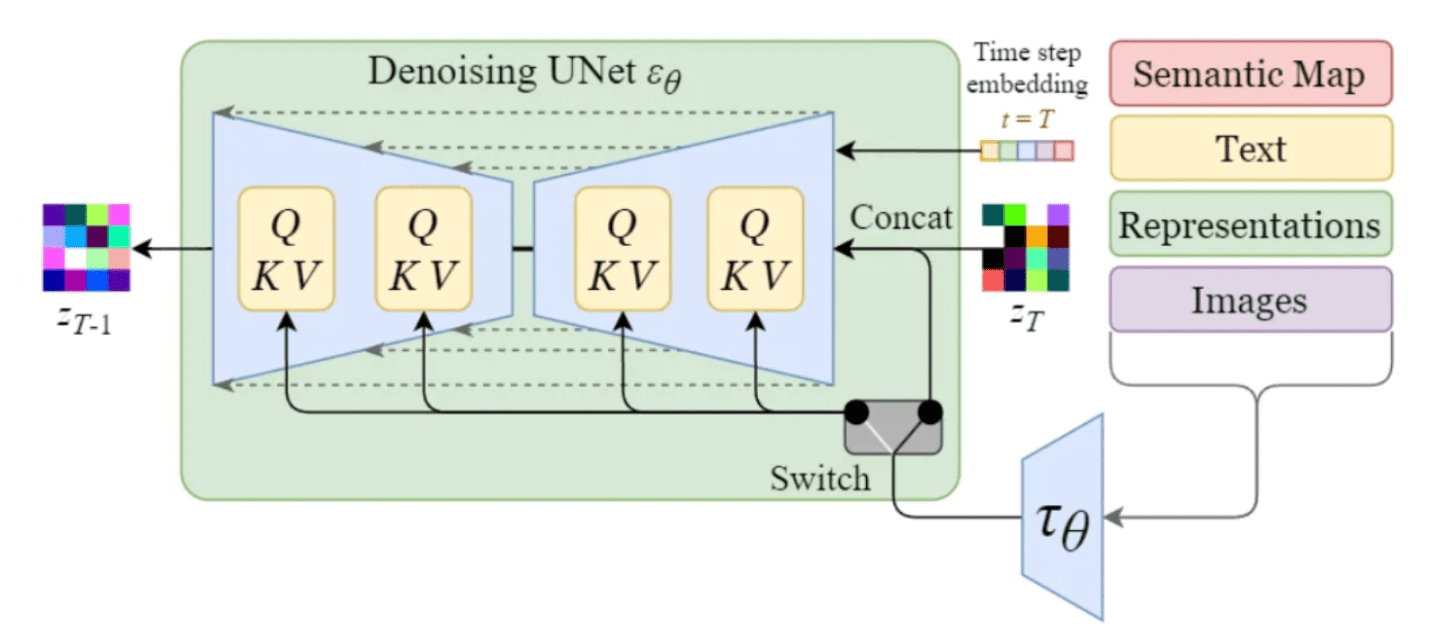
通过整合条件机制,稳定扩散模型扩展了其基于特定附加输入生成图像的功能。文本提示、语义图或附加图像可实现更加灵活和可控的图像合成。通过使用提示工程,可以创建更引人注目的图像。
架构
在探索潜在扩散模型和条件作用的过程中,可以注意到图像生成领域取得了显著的突破。现在,是时候看看稳定扩散的整个过程是什么样的了。
一方面,在训练过程中,图像(x 0 )通过编码器 E进行编码,得到图像的潜在表示(z 0)。在正向扩散过程中,图像会添加高斯噪声,从而得到噪声图像 (z T)。然后,图像通过 U-Net,以预测 z T中存在的噪声。通过正向扩散中添加的实际噪声与预测之间的比较,可以计算出前面提到的损失。利用计算出的损失,通过反向传播更新 U-Net 的参数。
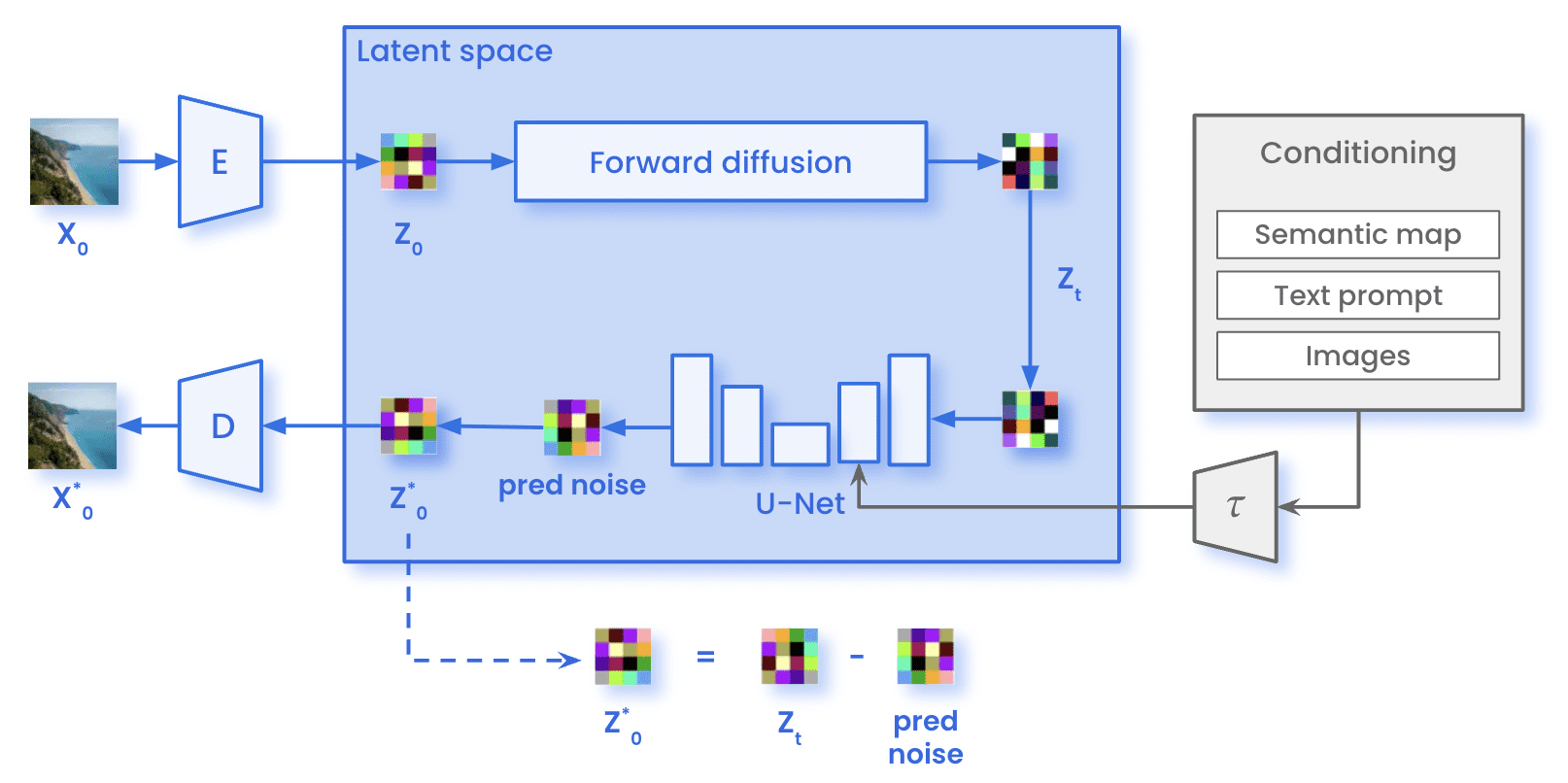
训练时稳定的扩散架构
另一方面,前向扩散过程不会在采样期间发生。仅对潜在空间 (z T ) 中存在的具有相同维度的高斯噪声进行采样。此噪声以指定的推理步骤 T 数通过 U-Net。在每个步骤t中,U-Net 都会预测图像中存在的全部噪声。该模型仅去除预测噪声的一小部分以获得时间步长t-1处图像的表示。在迭代完成所有 T 推理步骤之后,获得生成图像在潜在空间内的表示 (ẑ 0 )。然后使用解码器 D,可以将该图像从潜在空间转换为像素空间 (X̂ 0 )。
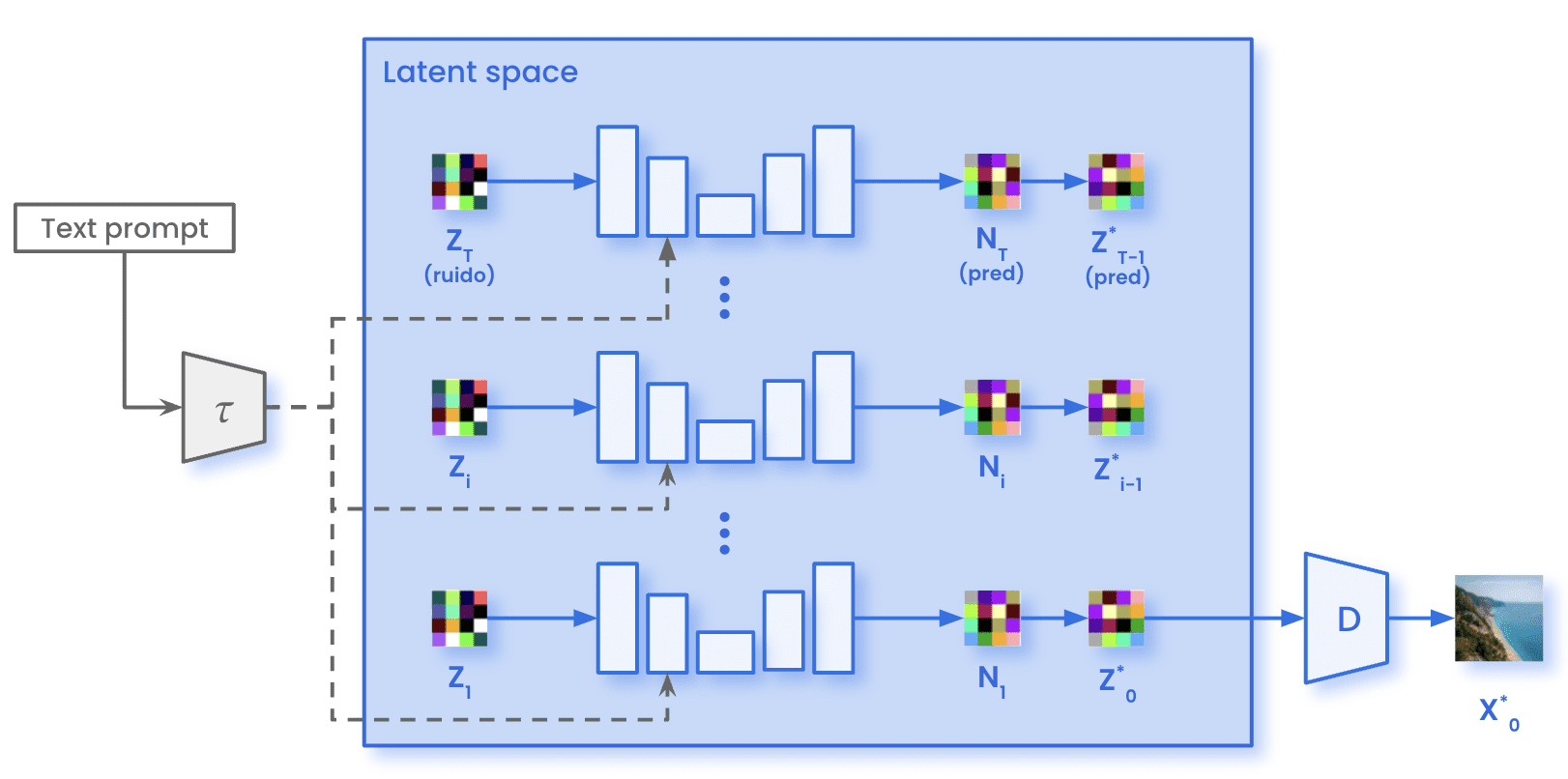
采样时稳定的扩散结构
使用案例
扩散模型提供了多种解决方案来解决各种问题。扩散模型最常用于以下情况:
- 通过提示生成图像:根据文本提示或条件输入生成图像,从而实现受控和可定制的图像合成。
- 图像超分辨率:增强低分辨率图像的分辨率和质量,生成具有增强细节和清晰度的高分辨率版本。
- 领域自适应和风格转换:将一个图像或领域的风格或特征转换到另一个图像或领域,使得在源域上训练的模型能够适应在具有不同视觉特征的目标域上表现良好。
- 图像修复:填充图像缺失或损坏的部分,重建缺失的细节以创建视觉上完整连贯的图像。
- 图像扩展:将图像扩展到其边界之外,从而创建连续性并生成更大的图像。

第一张图片是 可以实现的功能示例,取自其网页顶部。第二张图片展示了一个修复示例,将狗(通过修复)替换为猫(通过提示)
关键要点
总而言之,以下是希望您阅读本文后获得的关键要点:
- 扩散模型由两个过程组成:正向扩散和反向扩散。
- 前向扩散过程包括迭代添加高斯噪声。通过仅使用一个步骤的闭式公式,消除了迭代的需要。这可以更快地生成损坏的图像。
- 反向扩散过程是利用神经网络来近似去噪过程。这个过程是迭代的,一步一步,直到恢复原始图像。
- 潜在扩散模型 (LDM) 通过在潜在空间中执行扩散过程来提高基于扩散的图像生成的效率。这种方法显著加快了生成过程,特别是对于大图像和较长的扩散步骤。
- 一些传播模型提供了使用额外输入来引导生成的可能性。文本和图像是一些常见的引导输入。
- 扩散模型已在各种用例中得到应用。其中包括:通过提示生成图像、图像修复、域自适应/风格迁移和图像超分辨率。这些模型为从创意图像合成到图像增强和恢复等任务提供了多种解决方案。
标签:简介,模型,噪声,步长,图像,扩散,过程 From: https://www.cnblogs.com/changryJB/p/18657312