前言
更好的阅读体验。
无旋 treap。
默认读者会 BST 的基本操作、堆和旋转。
本文旋转部分和上面那篇文章的相同。
代码中是小根堆。
思想
treap 既是一棵二叉查找树(tree),也是一个二叉堆(heap)。
但是如果这两个数据结构用同一个权值维护,那么这两种数据结构是矛盾的。
所以 treap 用了一个很巧妙的方式:给每个节点附加一个随机的优先级,让权值满足二叉查找树的结构,让优先级满足二叉堆的结构。
这个就是一棵 treap(黑色是权值,蓝色是随机的优先级):
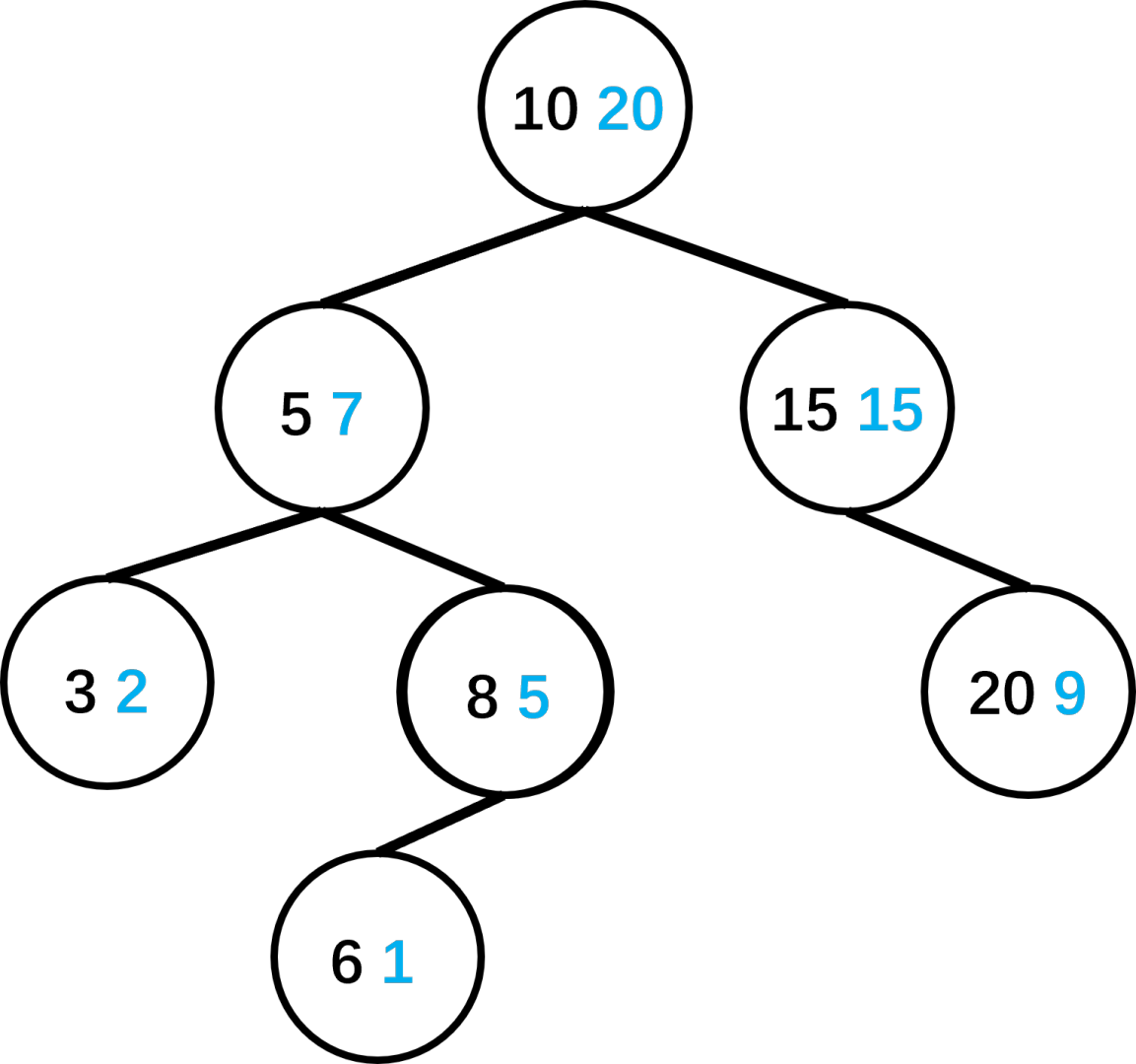
由于优先级只能随机赋予,堆不一定是一颗完全二叉树,,所以 treap 是弱平衡(近似平衡)的。
旋转
在不改变中序遍历的情况下,旋转可以改变树的结构。
在 treap 中,我们用旋转来满足二叉堆,控制树高。
图中从左到右是右旋,从右到左是左旋。
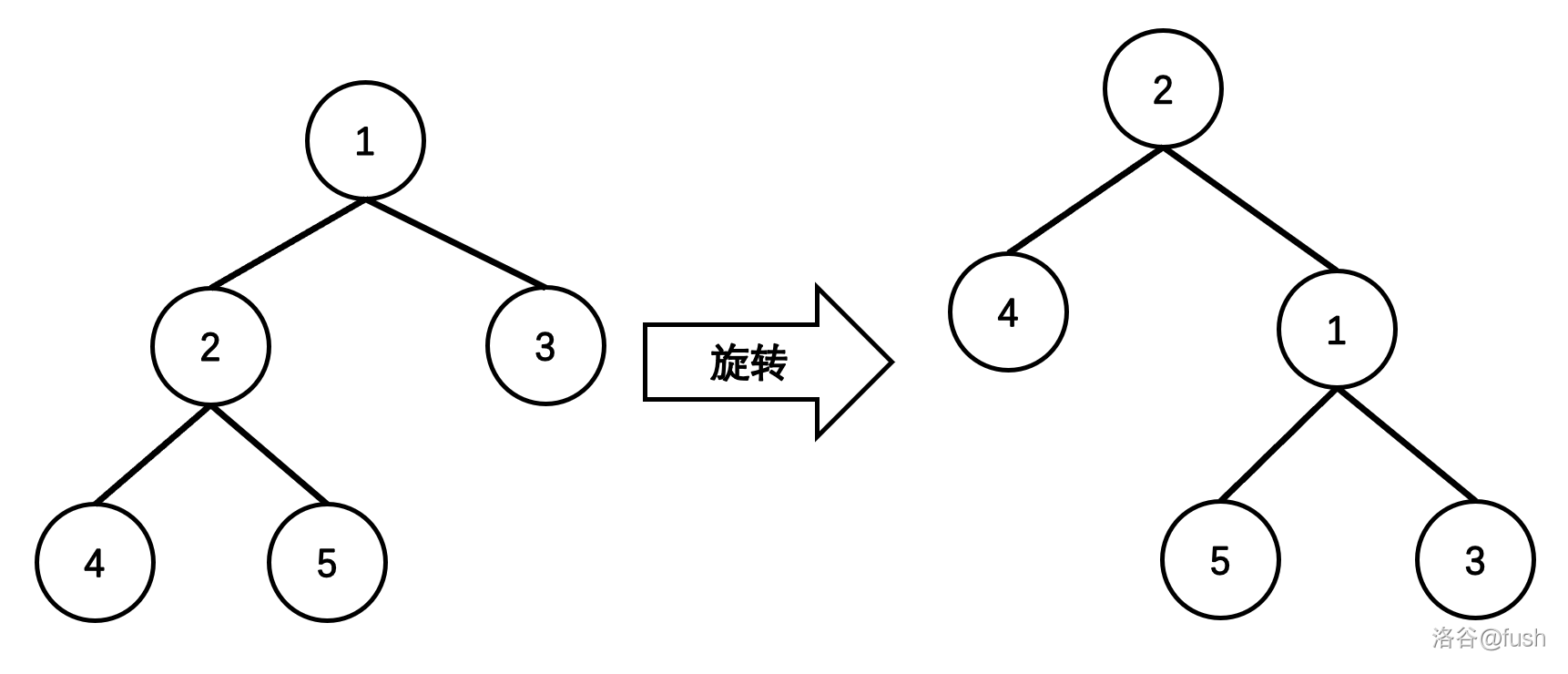
我们来模拟一下右旋的过程(左旋同理)。
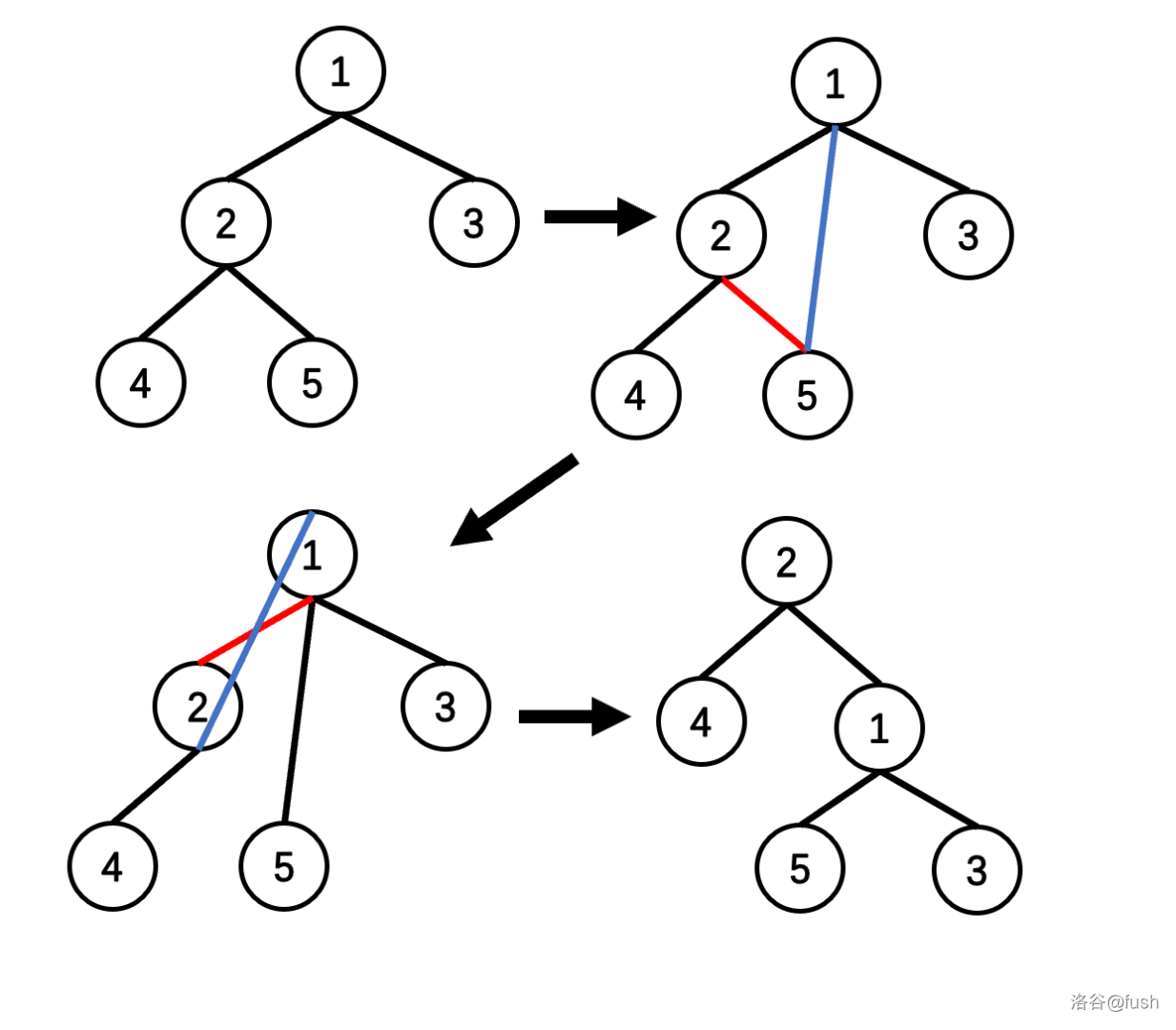
在实现中,我会把左右旋放在一起写。
void rotate(int&now, int dir){
int t = d[now].ch[dir];
d[now].ch[dir] = d[t].ch[!dir];
d[t].ch[!dir] = now;
pushup(now), pushup(t), now = t; //now 是 t 的儿子了,先更新 now 再更新 t
}
这里的 rotate(x, 0) 表示将 \(ls_{x}\) 提到 \(x\) 的高度,即右旋。
这里的 rotate(x, 1) 表示将 \(rs_{x}\) 提到 \(x\) 的高度,即左旋。
基础操作
节点变化
我们要在定义的时候添加一个优先级,然后在新建时给他赋随机值。
//需要头文件 <random>,<chrono>
std::mt19937 rd(std::chrono::steady_clock::now().time_since_epoch().count());
struct node{
int ch[2], size, val, rank;
}d[N];
int newnode(int x){
int w = ++tot;
d[w].val = x, ls(w) = rs(w) = 0, d[w].size = 1, d[w].rank = rd();
return w;
}
插入
只有在插入的那个子树的优先级可能变化。
如果优先级比当前节点小,那么我们把它旋转上来。
记得更新节点。
void insert(int&now, int val){
if(!now)return void(now = newnode(val));
int dir = d[now].val < val;
insert(d[now].ch[dir], val);
if(d[d[now].ch[dir]].rank < d[now].rank)rotate(now, dir);
if(now)pushup(now);
}
删除
这里我们需要改变一下目标节点有两个儿子的时候的方法。
我们比较两个儿子的优先级,把优先级小的旋转上来。
那么目标节点就到当前节点的另一侧,继续删除即可。
返回时要更新节点。
void del(int&now, int val){
if(!now)return;
if(d[now].val == val){
if(ls(now) && rs(now)){
int z = d[rs(now)].rank < d[ls(now)].rank;//哪边的优先级小
rotate(now, z), del(d[now].ch[!z], val);//删除另一侧
}
else now = ls(now) ? ls(now) : rs(now);
}
else if(d[now].val < val)del(rs(now), val);
else del(ls(now), val);
if(now)pushup(now);//牢记
}
代码
可持久化
不知道什么是可持久化的戳这。
只需要在所有要修改节点的地方新建节点,有注释的是新加句子。
完整代码。
修改片段:
void copynode(int &i){if(i)d[++tot] = d[i], i = tot;}//************
void rotate(int&now, int dir){
int t = d[now].ch[dir];
copynode(t);//************** now节点已经新建过了
d[now].ch[dir] = d[t].ch[!dir];
d[t].ch[!dir] = now;
pushup(now), pushup(t), now = t;
}
void insert(int&now, int val){
copynode(now);//****************
if(!now)return void(now = newnode(val));
int dir = d[now].val < val;
insert(d[now].ch[dir], val);
if(d[d[now].ch[dir]].rank < d[now].rank)rotate(now, dir);
if(now)pushup(now);
}
void del(int&now, int val){
copynode(now);//****************
if(!now)return;
if(d[now].val == val){
if(ls(now) && rs(now)){
int z = d[rs(now)].rank > d[ls(now)].rank;
rotate(now, z), del(d[now].ch[!z], val);
}
else now = ls(now) ? ls(now) : rs(now);
}
else if(d[now].val < val)del(rs(now), val);
else del(ls(now), val);
if(now)pushup(now);
}