原作:Stephen Wolfram
计算机视域下的时间
时间是人类经验的核心。然而,究竟什么是时间?在传统科学中,它常被比作空间坐标(尽管这种坐标对我们来说总是不断增长)。尽管这种描述在数学上可能很有用,但它并没有揭示时间的本质。
一旦我们开始用计算术语思考,就会觉得越来越接近。因为那时,我们会很自然地将世界的连续状态看作是通过逐步应用某些计算规则从上一个状态计算出来的。这暗示我们可以将时间的流逝与宇宙逐步进行计算的过程相对应。
但这仅仅意味着我们是在用“计算步数”来替换“时间坐标”吗?不是的。由于计算不可约性的存在。按照传统数学对时间坐标的理解,人们通常认为这个坐标可以“设定为任意值”,然后可以立即计算出系统在那个时刻的状态。然而,计算不可约性表明,事情并没有这么简单。它意味着,通常没有比通过逐个追踪系统演化的每一步更好的方法来预测系统将会如何发展。
左侧图片展示了计算可约简性,可以直观地预见到经过任意步数 t 后的状态。而右侧图片(可能)体现了计算不可约简性,要预测经过 t 步后的结果,实际上只能通过运行所有这些步骤来实现:

关于时间的本质
计算机视域下的时间
时间是人类经验的核心。然而,究竟什么是时间?在传统科学中,它常被比作空间坐标(尽管这种坐标对我们来说总是不断增长)。尽管这种描述在数学上可能很有用,但它并没有揭示时间的本质。
一旦我们开始用计算术语思考,就会觉得越来越接近。因为那时,我们会很自然地将世界的连续状态看作是通过逐步应用某些计算规则从上一个状态计算出来的。这暗示我们可以将时间的流逝与宇宙逐步进行计算的过程相对应。
但这仅仅意味着我们是在用“计算步数”来替换“时间坐标”吗?不是的。由于计算不可约性的存在。按照传统数学对时间坐标的理解,人们通常认为这个坐标可以“设定为任意值”,然后可以立即计算出系统在那个时刻的状态。然而,计算不可约性表明,事情并没有这么简单。它意味着,通常没有比通过逐个追踪系统演化的每一步更好的方法来预测系统将会如何发展。
左侧图片展示了计算可约简性,可以直观地预见到经过任意步数 t 后的状态。而右侧图片(可能)体现了计算不可约简性,要预测经过 t 步后的结果,实际上只能通过运行所有这些步骤来实现:
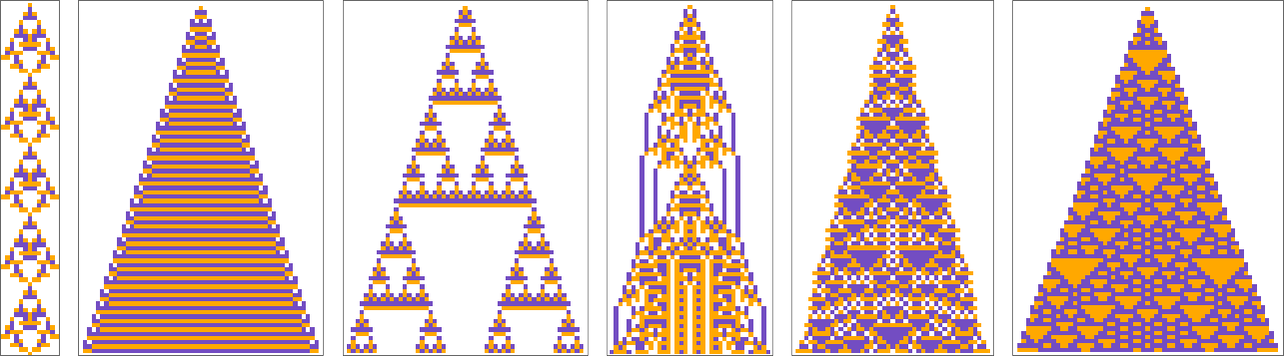
这意味着,从计算的角度来看,时间具有一定的稳定性。我们无法“跳跃”到未来;要了解未来会发生什么,唯一的方法就是通过不可减少的计算步骤逐步实现。
存在一些简单的理想化系统(例如,具有纯粹周期性行为的系统),在这些系统中存在计算可约性,且没有关于时间进程的稳健概念。然而,正如计算等价原理所暗示的那样,我们的宇宙必然充满了计算不可约性,这实际上定义了时间进程的稳健概念。
观察者角色的作用
那时,时间是宇宙计算进步的反映,这是一个重要的起点。但并非故事的终点。比如,这里有一个直接的问题:如果我们有一个规则可以决定系统的每个后续状态,那么在原则上我们至少可以预知系统的整个未来。那么,为什么我们只有“事情发生时才展开”的未来体验呢?
这主要是因为我们作为观察者的本质。如果基础系统在计算上不可还原,那么要预测其未来行为就需要不可还原的计算量。然而,我们这样的观察者有一个基本特点,那就是我们的计算能力有限。所以,我们无法完成所有这些不可还原的计算工作来“完全预知未来”——实际上,我们只能与系统同步进行计算,永远无法真正“领先一步”,只能看到未来“逐步呈现”。
本质上,我们之所以感知时间,是因为我们作为观察者的计算限制与宇宙基本过程的计算不可约性相互作用。如果我们不受计算限制,我们就能“一口吞下整个未来”,根本不需要时间这个概念。同样,如果没有基本的计算不可约性,也就不会有我们与时间体验相关的“未来的渐进展现”。
我们日常对时间的感知的一个显著特点是它似乎“只朝一个方向流动”——例如,记住过去通常比预测未来容易得多。这与热力学第二定律密切相关,而热力学第二定律(正如我在其他地方详细论述过的)又是底层计算不可约性和我们的计算有界性相互作用的结果。是的,微观物理定律可能是可逆的(事实上,如果我们的系统简单——并且计算可约——这种可逆性可能会“充分显现”)。但关键是,计算不可约性在某种意义上是一种更强大的力量。
假设我们准备一个有序结构的态。如果其演化在计算上不可还原,那么这种结构将有效地被“加密”,以至于计算有限的观察者无法识别。由于基本可逆性,这种结构在某种意义上不可避免地“仍然存在”,但计算有限的观察者无法访问它。因此,这样的观察者会感觉到从有序到无序的明确转变。(理论上,人们可能会认为可以设置一个表现出“反热力学”行为的态——但关键在于,这样做需要预测一个计算上不可还原的过程,而计算有限的观察者无法完成这一预测。)
关于时间的本质长期以来存在的一些混淆,与它对空间的“数学相似性”密切相关。实际上,自相对论理论初期起,将空间和时间概念合并为“时空”的说法就显得十分便利。
但在我们的物理项目中,事情的基本运作方式并非如此。在最低层次上,宇宙的状态由一个超图来表示,这个超图捕捉了可以被视为离散“空间原子”之间的“空间关系”。时间则对应于这个超图的逐步重写。这样的表述更加自然和易于理解。
在某种意义上,“时间的原子”是发生的根本“重写事件”。如果一个事件的“输出”需要作为另一个事件的“输入”,那么我们可以认为第一个事件在时间上先于第二个事件——事件之间具有“时间分离”的特性。通常,我们可以绘制一个因果图,展示不同事件之间的相互依赖关系。
如下所述,我们日常对时间的体验是它遵循一条单线程。因此,我们倾向于将基本事件的因果图“解析”成一系列切片,我们可以将其视为对应于“相继的时间”。在标准相对论中,通常没有一种独特的方式来分配这样的“同时性表面”序列,因此存在不同的“参考系”,在这些参考系中,空间和时间的识别方式各不相同。这样的表达更加自然,易于理解。
完全因果图将我们通常认为的空间与我们通常认为的时间捆绑在一起。但最终,时间的进展总是与一些“在计算上相互建立”的连续事件的选择有关。是的,由于存在不同的选择,它变得更加复杂。但时间进展作为“计算的进行”的基本思想是非常相似的。(从某种意义上说,时间代表宇宙中的“计算进展”,而空间代表“其数据结构的布局”。)
正如从分子动力学推导出第二定律(或流体力学)的过程一样,从超图重写的底层因果图推导出描述时空大尺度行为的爱因斯坦方程,依赖于我们是计算受限的观察者。尽管如此,我们内部仍然需要“有所活动”,否则我们就无法记录或感知到任何“时间上的进展”。
看起来这是我们这类观察者本质的体现——正如我在最近的《观察者理论》中所阐述的——我们将许多不同的世界状态视为等价,以此来推导出我们对“外界发生了什么”的内在感知。在某种程度上,我们可能会想象,我们通过不断更新这些内在感知来感知时间的流逝。如果我们不再更新感知,那么对我们来说,时间实际上就会停止——就像我们睡觉、麻醉或死亡时那样。
值得注意的是,在某些极端情况下,时间停止并非由观察者的内部结构造成,而是宇宙本身的底层结构所致。正如我们之前提到的,“宇宙的演化”与底层超图的连续重写有关。然而,当超图中“活动过于频繁”(这在物理上大致等同于能量-动量过多)时,就会产生“无法再进行重写”的情况——因此,实际上宇宙的一部分将无法继续发展,时间在那里停滞。这类似于传统广义相对论中时空奇点(通常与黑洞相关)的现象。 但现在它有一个非常直接的计算机解释:一个人已经达到了“固定点”,此时不再需要进行计算。因此,在时间上不再有进步的可能。
时间的多重线索
我们强烈的人类经验是,时间如同一条单线程不断向前推进。然而,我们的物理项目指出,在更深层次上,时间实际上是以多线程的形式存在,也就是说,宇宙遵循着多条不同的“历史路径”。正是由于我们作为观察者以这种方式对事物进行采样,我们才将时间感知为一条单线程。
在特定底层超图的层面上,可能存在许多不同的更新事件,每个这样的更新事件的序列定义了不同的“历史路径”。我们可以将这些历史路径总结在一个多向图中,将出现的相同状态合并起来:

然而,考虑到这种基础结构,我们作为观察者为何认为时间是一条单线程的呢?这一切都与分支空间的概念以及我们在其中的位置有关。众多历史路径的存在导致了量子力学;我们作为观察者最终只感知到一条路径,这与量子力学中传统上颇为神秘的“测量”现象紧密相连。
当我们之前讨论因果图时,提到可以将它们解析为一系列对应于瞬时“空间状态”的“时空”切片,由空间超图表示。类比之下,我们也可以想象将多向图分解成“瞬时切片”。然而,这些切片不再代表普通空间的状态,而是代表我们所说的分支空间的状态。
普通空间是通过更新对其他事件产生因果影响的事件来“编织”在一起的,这些事件仿佛位于空间的不同位置。或者说,空间就像是通过不同事件的元素光锥的重叠来“编织”在一起。现在,我们可以将分支空间理解为通过更新对最终落在不同历史分支上的事件产生影响的事件来“编织”在一起。
通常,普通空间与分支空间之间有着紧密的相似性,我们可以构建一个包含“时空”和“分支”方向的多元因果图。在这个图中,分支方向并不支持光锥,而是我们所说的纠缠锥。
我们作为观察者,如何理解正在发生的事情呢?一个关键点是,我们不可避免地成为了我们所观察系统的组成部分。因此,整个系统中的分支(以及合并)过程也在我们自身中发生。这意味着我们需要思考一个“分支思维”会如何感知一个“分支宇宙”。在底层,存在着众多分支和“历史线索”。同时,还存在着许多计算不可约性,甚至可以说是多计算不可约性。然而,像我们这样的计算能力有限的观察者,必须将这些细节进行等价化处理,以便在有限的大脑中找到合适的解释。
我们可以将这种现象比作气体中的情况。在底层,众多分子在四处弹跳(并以无法用计算还原的方式行动)。然而,与分子相比,我们这样的观察者体型庞大,因此无法观察到它们的个体行为,只能感知它们的整体行为——并从中提取出一些微小的、可计算上简化的“流体动力学级别”特征,使其更加自然易懂。
空间的底层结构基本上是一样的。在底层,有一个复杂变化的离散空间原子网络。然而,作为大型、计算受限的观察者,我们只能采样聚合特征,其中许多细节已被等价化,空间往往显得连续,并且可以用基本可计算的途径来描述。
那么,关于分支空间呢?嗯,基本上是同样的情况。我们的思维“很大”,在历史的角度来看,它们覆盖了许多个体分支。由于计算上的限制,它们无法感知所有这些分支的细节,只能感知一些综合特征。在初步估计中,最终呈现出来的是一个单一的历史线索。
通过足够细致的测量,我们有时能观察到“量子效应”,此时多个历史线索并存。然而,在直接的人类层面,我们似乎总是将事物汇聚到一定程度,以至于我们所感知到的只是单一的历史线索——或者说,实际上是时间进程中的单一线索。
这些“聚合”是否有效并不一目了然。我们感知到的气体中的重要效应可能依赖于单个分子的现象。或者,要理解空间的宏观结构,我们可能需要持续关注空间原子的具体特征。同样,我们可能永远无法维持“一致的历史观”,而总是需要追踪众多历史线索。
但是关键在于,作为计算受限的观察者,我们必须挑选出那些可以计算简化的特征——或者说,实际上是可以有限度地描述的简单特征。
与我们的计算边界密切相关的是,我们做出的一个重要假设:作为观察者,我们具有某种持续性。在每一个时刻,我们由不同的空间原子和多元图中的不同分支构成。但我们仍然相信,我们还是“同一个我们”。而一个关键的物理事实(必须在我们的模型中推导出来)是,在正常情况下,这样做并不会产生矛盾。
因此,尽管在最底层存在许多“时间线”——代表着许多不同的“量子分支”——但像我们这样的观察者(通常)仍然能够将其视为一个单一的、连贯的感知时间线。
但这里还有另一个问题。说单个观察者(比如单个人类思维或单个测量设备)可以感知历史遵循单一、一致的线索是一回事。但不同的人类思维或不同的测量设备呢?他们为什么要感知任何一致的“客观现实”?
我认为答案的本质在于,它们在分支空间中足够接近。如果我们从物理空间的角度来看,宇宙不同区域的观察者显然会“看到”不同的事情发生。物理定律可能相同——但附近的恒星(如果有)会有所不同。但至少在可预见的未来,对我们所有人来说,总是同一颗恒星是最近的。
然而据推测,这同样适用于分支空间。我们人类——有着共同的起源——存在于一个小小的区域。可能正是因为这个区域相对于整个分支空间来说很小,所以我们才都感受到了一个连贯的历史线索和共同的现实。
这其中有很多细微之处,其中许多尚未完全解决。在物理空间中,我们知道效应原则上可以以光速传播。而在分支空间中,类似的现象是效应可以以最大纠缠速度传播(虽然我们不知道具体数值,但它与普朗克单位转换有关,与基本长度和基本时间相关)。然而,为了保持我们共同的“客观”宇宙观,我们都不应该以光速向不同方向分散。当然,之所以不会发生这种情况,是因为我们并非没有质量。实际上,非零质量可能是我们这类观察者不可或缺的一部分。
在我们的物理项目中,超图中事件的密度决定了物理空间中能量(以及质量)的密度(及其相关的引力效应)。同样,多向图或分支图切片中事件的密度决定了作用的密度——这是在分支空间中与能量相对不变的对立面(及其对量子相的影响)。尽管目前尚不清楚其具体机制,但似乎可以推测,当存在质量时,效应不会像“以所有方向的最大纠缠速度发散”那样消失,而是会停留在附近。
肯定存在“停留在同一地点”、“相信自己是持久的”和“计算受限”之间的联系。这些因素似乎是形成我们对时间单线程观念的必要条件。从理论上讲,我们可以设想与我们截然不同的观察者——例如,拥有(类似于理想化量子计算机内部的)能够体验众多历史线程的头脑。然而,计算等价原理指出,这样的观察者需要具备很高的能力。他们不仅要能够处理计算不可约性,还要能够处理多计算不可约性,即同时处理计算新状态和等价状态的过程。
对于“类似我们”的观察者而言,我们可以预见,时间将再次倾向于按照我们通常所经历的方式,沿着一条单一的线索发展,并在观察者之间保持一致性。
值得注意的是,这一切仅适用于我们这样的观察者,在类似我们的情况下。例如,在黑洞的“纠缠视界”处——多向因果图中的分支定向边缘被“困住”——从某种意义上说,我们所熟知的时间似乎“分解”了,因为观察者将无法将历史的各个分支“编织”在一起,形成一个关于发生事件的连贯的经典观念。
Ruliad 中的时光
到目前为止,我们讨论的内容中,我们可以将时间的进步看作是与反复应用规则相关联,这些规则逐渐“重塑宇宙的状态”。在上一节中,我们了解到这些规则可以以多种方式应用,进而产生许多不同的历史脉络。
但是,ruliad 在这里发挥作用。因为 ruliad 不涉及任何这样的看似任意的选择:它是遵循所有可能的计算规则后得到的结果。但到目前为止,我们一直认为应用的规则总是相同的,这让我们对“为什么是这些规则,而不是其他规则?”感到困惑。
可以设想出许多鲁利亚德的基础。可以将其构建于所有可能的超图重写之上,或者所有可能的多路图灵机之上。但最终,它是一个单一、独特的事物:所有可能计算过程的纠缠极限。在鲁利亚德中,“某处可能发生任何事情”有着某种含义。然而,赋予鲁利亚德结构的是,所有可能发生的事情以一种明确的(本质上几何的)方式排列和连接,这种排列和连接方式是确定的。
那么,我们如何认识鲁利亚德呢?我们不可避免地成为了鲁利亚德的一部分,因此我们从“内部”进行观察。然而,关键在于,我们对鲁利亚德的认知取决于我们作为观察者的特性。令人惊讶的是,在过去的几年里,仅仅对我们作为观察者的特性进行一些假设,就暗示了我们对鲁利亚德的认知遵循我们所熟知的物理学基本定律。换句话说,通过假设我们作为观察者的特性,我们实际上可以推导出我们的物理定律。
所有这一切的关键在于 ruliad 中底层行为的计算不可约性以及我们作为观察者的计算限制(以及我们关于自身持续存在的假设)之间的相互作用。正是这种相互作用产生了统计力学的第二定律、时空结构的相对论方程,以及我们认为的量子力学的路径积分。实际上,我们的计算限制作为观察者使我们能够将事物等价化,以至于我们只能观察到 ruliad 的计算可约部分,这些部分可以用已知的物理定律来描述。
那么,时间在这个体系中如何定位呢?Ruliad 的一个核心特征是其独特性——它的一切都是“抽象必要”的。就像给定数字的定义、加法和等式,1 + 1 = 2 是不可避免的,同样地,给定计算的定义,Ruliad 也是不可避免的。换句话说,Ruliad 的存在是不容置疑的;它只是从抽象定义中自然而然产生的抽象构造。
在某种程度上,这意味着 ruliad 不可避免地“作为一个完整的事物而存在”。所以,如果能够“从外部观察”,那么就可以将其看作是一个单一的永恒物体,没有时间的概念。
但是关键在于,我们无法从“外部”去“观察”它。我们身处其中。而且,更重要的是,我们必须通过“计算限制”的“透镜”去观察它。这也是我们不可避免地得出时间概念的原因。
我们从鲁利亚内部某个点观察它。如果不受计算限制,我们就能立刻计算出整个鲁利亚的形态。然而实际上,我们只能“一步一步地”去发现鲁利亚——“逐个应用有限的计算”来“在规则空间中逐步前进”。这样的描述更加自然易懂。
即使在某种抽象意义上“整个鲁利亚已经存在”,我们却只能一步步去探索它。这种探索过程形成了我们对时间的认识,也是我们不断前进的动力。
不可避免地,我们可以通过 ruliad 探索许多不同的路径。实际上,每个心灵(包括我们这样的观察者)——带着其独特的内在体验——可能都选择了不同的路径。但正如我们在描述分支空间时所说,我们之所以有一个共同的“客观现实”概念,可能是因为我们在 rulial 空间中彼此非常接近;从某种意义上说,我们形成了一个紧密的“rulial 鸟群”。
值得注意的是,并非所有我们能够方便获取的 ruliad 样本都对应于对时间渐进切片的探索。是的,这种“时间上的渐进”正是我们物理体验的特征,也是我们描述它的常见方式。那么,我们的数学体验又是怎样的呢?
首先需要强调的是,鲁利亚不仅包含了所有可能的物理学,也包含了所有可能的数学。如果我们以超图为起点构建鲁利亚,那么现在的节点就不再是“空间的基本单位”,而是抽象元素(我们通常称之为 emes),这些元素构成了数学表达式和定理的组成部分。我们可以将这些抽象元素视为现在不是分布在物理空间中,而是在一个抽象的元数学空间中排列。
在我们的物理体验中,我们通常局限于物理空间、鳃空间等。然而,在从事数学活动时,我们似乎是在元数学空间中不断拓展,划分出一些“我们认为是真的定理”的领域。尽管我们可以找到一种“扩展路径”来定义时间的类比,但这并非我们探索 ruliad 所必需的属性。
在某种意义上,ruliad 中的不同地方对应于用不同的规则来描述事物。类比于物理空间中的运动概念,我们可以通过将一组规则的计算转换为另一组规则的计算,有效地在 ruliad 中“移动”到另一个地方。是的,即使有“纯粹运动”的可能性也是非平凡的。但如果我们确实在 ruliad 中保持本地化(并且能够维持我们所谓的“连贯身份”),那么想到存在一条“运动路径”,我们沿着这条路径“随着时间的推移”前进,这是很自然的。 但是当我们仅仅是为了拓宽视野,将更多范式和 rulial 空间纳入我们的思维覆盖范围(从而实际上是在拓宽 rulial 空间)时,这并不是同一个故事。我们并没有把自己视为“为了移动而进行计算”。相反,我们只是在识别等价关系,并利用这些关系来扩展我们对自己的认识,这至少可以类比为传统物理学中的“量子测量”那样,看作是“超越时间”发生的。然而,最终,所有发生的事情都必须是计算的结果。只是我们通常不会将这些计算“打包”成明确的时间线。
到头来,时间究竟是什么?
从我们在此讨论的范式(以及物理项目想法)出发,关于“时间是什么?”这个问题在某种程度上很简单:时间是在应用计算规则时不断前进的。但关键在于,时间可以抽象地定义,与这些规则的细节或它们所依赖的基础无关。而这一切得以实现,正是得益于计算等价原理以及它所蕴含的普遍现象——计算不可约性。
首先,将时间视为线性链条式的“前进”,这一观点源于计算不可约性——因为正是计算不可约性告诉我们,像我们这样的计算能力有限的观察者无法一般性地“跳跃”到未来;我们只能按部就班地跟随这一线性步骤序列。
但是,除了这个之外,还有其他因素。计算等价原理表明,在某种意义上,只存在一种(普遍存在的)计算不可约性。因此,当我们观察遵循不同不可约计算规则的不同系统时,它们的行为不可避免地具有某种普遍性。实际上,它们都以相同的方式积累计算效应。或者说,它们以相同的方式随着时间的推移而发展。
这里与热量的类比非常紧密。可能存在详细的分子运动,即便在宏观尺度上,不同材料中的运动也可能存在显著差异。但事实上,我们只需说这种运动代表了一定的热量,就能描述任何这样的运动,无需深入细节。这和说一定时间已经过去,无需深入了解反映时间流逝的时钟或其他系统的具体工作方式非常相似。
事实上,这里并不仅仅是一个“概念类比”。因为热现象本身就是计算不可约性的结果。而它具有统一的、“抽象”的描述,这恰恰体现了计算不可约性的普遍性。
再次强调,正如与热量一样,一个强大的时间概念依赖于我们作为计算受限的观察者。如果不是这样,我们就能通过详细计算分子过程来违反第二定律,而不会仅仅用随机性和热量来描述事物。同样,我们也能打破时间的线性流动,要么向前跳跃,要么跟随不同的时间线索。
但作为计算能力有限的观察者,面对无法简化的计算过程,我们几乎不可避免地会近似地将其视为一条单一的一维时间线。
在传统基于数学的科学中,人们常常觉得目标应该是“预测未来”——或者说实际上是要“超越时间”。然而,计算不可约性告诉我们,通常我们无法做到这一点,而要了解将会发生什么,唯一的方法就是逐步运行与系统本身相同的计算。虽然这可能会让人对科学的威力感到失望,但这也正是赋予时间意义和重要性的原因。如果我们总能提前一步,那么在某种程度上,时间的流逝(或者说,我们生活的过程)将永远无法从根本上取得任何成就;我们总能说出会发生什么,而无需“经历”如何到达那里。 但计算不可约性赋予了时间和其传递过程一种坚硬、具体的特点。
那么,这一切对我们通常讨论时间的方式中出现的各种经典问题以及明显悖论意味着什么呢?
那么,这对于通常讨论时间的方式中出现的各种经典问题(以及明显的悖论)意味着什么呢?
让我们从可逆性问题开始。传统的物理定律基本上适用于时间的向前和向后。而ruliad不可避免地在“前向”和“后向”规则之间是对称的。那么,为什么在我们的典型经验中,时间似乎总是“朝着同一个方向运行”呢?
这与第二定律密切相关,也是我们的计算有界性与潜在的计算不可约性相互作用的结果。从某种意义上说,为我们定义时间方向的是,我们(通常)发现记住过去比预测未来容易得多。当然,我们并不记得过去的每一个细节。我们只记得“适合我们有限思维”的某些“过滤”特征。当谈到预测未来时,我们因无法“超越”计算不可约性而受到限制。
让我们回顾一下第二定律是如何运作的。它基本上说,如果我们设置某种“有序”或“简单”的状态,那么它往往会“降级”为“无序”或“随机”的状态。 (我们可以认为系统的进化有效地“加密”了我们起始状态的规范,以至于我们——作为计算有限的观察者——无法再识别其有序起源。)但是因为我们的基本定律是可逆的,所以这个当我们在时间上向前和向后移动时,必然会发生降级(或“加密”):

但是关键在于,我们对于时间方向的经验定义(其中“过去”是我们所记忆的,“未来”是我们难以预测的)必然与我们在整个世界中观察到的热力学时间方向相一致。原因在于,在这两种情况下,我们都在将过去定义为一种计算上有限的状态(而未来则可能是计算上不可还原的)。在经验情况下,过去之所以是计算上有限的,是因为这是我们能够记住的;在热力学情况下,它之所以是计算上有限的,是因为这是我们能够制备的状态。换句话说,“时间之箭”之所以一致,是因为在这两种情况下,我们实际上都在“要求过去更加简单”。
那么,关于时间旅行呢?这个概念似乎很自然——也许甚至可以说是必然的——如果我们认为“时间就像空间一样”。但当我们以这种方式思考时间时,它就变得不那么自然了:将其视为一种应用计算规则的过程。这样的表述可能更符合中文的表达习惯。
在最低层面,这些规则按照定义只是顺序应用,一个状态接着一个状态产生——实际上是在时间中单向前进。但如果考虑的不仅仅是原始的最低层面规则,而是它们可能产生的实际效果,事情就会变得更加复杂。比如,如果规则导致的状态与之前产生的状态相同(比如在具有周期性行为的系统中),那么如果我们把现在和之前的状态视为等价(即我们将其视为同一个状态),那么我们可能会在我们的因果图中形成一个循环(即“封闭类时曲线”)。是的,从应用规则的原始顺序来看,这些状态可以被认为是不同的。 但是关键在于,如果它们在各个方面都一模一样,那么任何观察者都会自然而然地认为它们是相同的。
但是这样的等效状态真的会实际发生吗?只要存在计算不可约性,状态永远无法完美匹配几乎是必然的。实际上,对于状态中要包含像我们这样的观察者(具有“记忆”等)来说,它们能够匹配几乎是不可能的。
但是,能否想象一个观察者(或“时间工匠”)能够引导到与之匹配的状态?或许它能够小心翼翼地挑选出空间(或基本事件)的特定序列,从而引导它到达“之前发生过的”状态。确实,在一个计算简单的系统中,这可能是有可能的。但是,一旦出现计算不可约性,这就不是任何计算受限的观察者能够做到的事情了。是的,这正是为什么不能存在一个“麦克斯韦妖”观察者来“违反第二定律”。同样,这也解释了为什么不能存在一种能够小心翼翼地探索空间最基本结构,从而实现超光速旅行的东西。
即使不能实现“观察者时间倒流”的时间旅行,但“感知时间”仍可能因相对论效应(如与运动相关的效应)而发生变化。例如,一个经典的相对论效应是时间膨胀,即物体运动越快,“时间流逝越慢”。确实,在一定的假设下,这一效应可以通过直接的数学推导得出。然而,在我们探索时间的本质时,我们不禁要思考其背后的物理机制。结果令人惊讶,在我们的物理项目中,这一机制的解释既直接又近乎“机械”。
从这样一个事实出发,在我们的物理项目中,空间及其所有事物都由一个不断被重写的超图来表示。物体的演化是通过这些重写来定义的。然而,如果物体移动,那么实际上它必须在空间中的不同位置“重新生成”——这个过程需要一定数量的重写,这会减少留给物体自身内在演化的重写,因此导致时间对它来说实际上“流逝得更慢”。(是的,虽然这是一个定性的描述,但可以使其非常正式和精确,并恢复相对论时间膨胀的常用公式。)
类似的现象也出现在引力场中。在我们的物理项目中,能量-动量(以及引力)与底层超图的活跃度密切相关。这种活跃度的增加会导致更多的重写,使得该空间区域内的任何物体都会出现“时间加速”的现象(这与传统的“引力红移”相对应)。
这种现象在黑洞的背景下尤为明显。(实际上,我们可以将时空奇点类比为“时间飞逝至此终结”的地方。)此外,正如我们之前讨论的,存在许多“相对论效应”,在这些效应中,空间和时间以各种复杂的方式交织在一起。
即使在更为平凡的水平上,对于我们这样的观察者来说,空间和时间之间也存在某种至关重要的关系。关键在于,我们这样的观察者往往将世界“分解”为一系列“空间状态”,这些状态依次出现在“时间点”上。然而,我们之所以这样做,是因为我们具有一些非常具体的特征,尤其是与时间相比我们在空间中的有效物理尺度。
在我们的日常生活中,我们通常观察的是距离我们可能达数十米的场景。由于光速,这些物体的光子到达我们这里不到一微秒。然而,我们的大脑需要毫秒级的时间来处理我们所看到的。这种时间上的差异让我们觉得世界是由连续时间点上的空间状态序列组成的。
如果我们的脑部运作速度达到百万倍(即电子速度),我们就会感知到来自场景不同部分的 光子 在不同时间到达,我们可能就不再以连续时间中的空间整体状态来感知世界了。
如果我们保持大脑速度不变,却要应对更大规模的场景(正如我们在处理宇宙飞船、天文学等领域所做的那样),情况也会如此。
虽然这影响了我们对于时间“作用”对象的认知,但最终并未改变时间的本质。时间依旧是通过计算产生世界连续状态的过程。计算不可约性使得时间对于像我们这样的计算有限观察者来说具有了一定的刚性。而计算等价原理则允许存在一个独立于“基础”的稳健时间概念:无论是我们作为观察者,日常物理世界,还是整个宇宙。
标签:视角,观察者,本质,时间,计算,约性,空间,我们 From: https://www.cnblogs.com/Leap-abead/p/18638587/on-the-nature-of-time