如何评价 OI 赛制无 pretest 仅有至多两个 CF 同等强度的极小样例?
340->170 是最好的答案。
A.括号序列
每个括号找出和它匹配的括号,同时求出 \(pre_i\) 和 \(nxt_i\) 分别代表与 \(i\) 同层的前缀括号匹配数和后缀括号匹配数,那么当前层给 \(i\) 贡献为 \((pre_i+1)\times(suf_{r_i}+1)\),差分维护就好。
点击查看代码
#include <bits/stdc++.h>
#define fr first
#define se second
#define Un unsigned
#define LL long long
#define pb push_back
#define pii pair<int,int>
#define pLi pair<LL,int>
#define pLL pair<LL,LL>
#define __ __int128
#define LD long double
#define VE vector<LL>
#define DB double
#define Ve vector<int>
using namespace std;
const int P = 1e9+7,N = 1e7+5;
int stk[N],top,pre[N],suf[N],l[N],r[N];
LL a[N];
int main()
{
freopen("bracket.in","r",stdin);
freopen("bracket.out","w",stdout);
ios::sync_with_stdio(0);
string s;cin >> s;int n = s.size();
for (int i = 0;i < n;i++)
{
if (s[i] == '(') stk[++top] = i+1;
else if(top) r[stk[top]] = i+1,l[i+1] = stk[top],top--;
}
for (int i = 1;i <= n;i++)
if (s[i-1] == ')' && l[i]) pre[i] = pre[l[i]-1]+1;
for (int i = n;i >= 1;i--)
if (s[i-1] == '(' && r[i]) suf[i] = suf[r[i]+1]+1;
for (int i = 1;i <= n;i++)
if (s[i-1] == '(' && r[i]) a[i] += 1LL*(pre[i-1]+1)*(suf[r[i]+1]+1),a[r[i]+1] -= 1LL*(pre[i-1]+1)*(suf[r[i]+1]+1);
LL ans = 0;
for (int i = 1;i <= n;i++) a[i] += a[i-1],ans = ans+(a[i]*i)%P;
cout << ans;
return 0;
}
B.序列划分
设 \(h_i\) 表示 \(1\sim i\) 字符构成的十进制数字,即 \(h_i=\sum\limits_{j=1}^{i}s_i10^{i-j}\) 。
一个子串 \([l,r]\) 构成的十进制数字能整除 \(D\) 当且仅当 \(h_r-h_{l-1}\times10^{r-l+1}\equiv0\pmod D\) ,也就是说 \(h_r\equiv h_{l-1}\times10^{r-l+1}\pmod D\)。
设 \(f_i\) 为以 \(i\) 为结尾子串不能被 \(D\) 整除的前 \(i\) 个字符的划分方案数,\(g_i\) 为以 \(i\) 为结尾子串能被 \(D\) 整除的前 \(i\) 个字符的划分方案数,
每次转移 \(f_i=\sum\limits_{h_i-h_{j-1}\times10^{i-j+1}\not\equiv0\pmod D}g_j\),\(g_i=\sum\limits_{h_r-h_{l-1}\times10^{r-l+1}\equiv0\pmod D}f_j+g_j\)。
暴力向前扫是 \(O(n^2)\) 的,考虑优化。
若 \(\gcd(10,D)=1\),那么上述同余方程可以写成 \(h_r\times10^{-r}\equiv h_{l-1}\times10^{-(l-1)}\pmod D\),将 \(f_i,g_i\) 放进 \(h_i\times10^{-i}\) 对应桶里,每次查询桶里数的和即可。
若 \(\gcd(10,D)\neq1\),这时候 \(10\) 在\(\mod D\) 意义下没有逆元,不能用上述方法。
将 \(D\) 分解为 \(2^x5^yz\) 的形式。
那么同余方程可以分解为两个:
\(\begin{cases}h_r\equiv h_{l-1}\times10^{r-l+1}\pmod {2^x5^y}\\h_r\equiv h_{l-1}\times10^{r-l+1}\pmod {z}\end{cases}\)
如果要满足 \([l,r]\) 构成的十进制数字能整除 \(D\),必须同时满足上方两个式子。
由于 \(D\) 最大是 \(10^6\),也就是说 \(\max(x,y)\le20\),所以 \(r-l+1\ge20\) 的时候,\(h_{l-1}\times10^{r-l+1}\equiv0\pmod {2^x5^y}\)。
此时需要判断的条件就变成了:
\(\begin{cases}h_r\equiv 0\pmod {2^x5^y}\\h_r\equiv h_{l-1}\times10^{r-l+1}\pmod {z}\end{cases}\)
而 \(\gcd(10,z)=1\) ,套用 \(\gcd(10,D)=1\) 的方法就行了。
而当 \(r-l+1 < 20\) 的时候不能这么做,这部分暴力向前扫 \(20\) 个就行了。
代码写的有点繁。
点击查看代码
#include <bits/stdc++.h>
#define fr first
#define se second
#define Un unsigned
#define LL long long
#define pb push_back
#define pii pair<int,int>
#define pLi pair<LL,int>
#define pLL pair<LL,LL>
#define __ __int128
#define LD long double
#define VE vector<LL>
#define DB double
#define Ve vector<int>
//Keep your mind clear.
using namespace std;
const int N = 5e5+5,P = 1e9+7;
int f[N],g[N],F[N<<1],G[N<<1];
LL h[N],B[N],pw[N],H[N];
inline int mod(int x){return x >= P ? x-P : x < 0 ? x+P : x;}
void exgcd(int a,int b,int &x,int &y)
{
if (!b) return (void)(x = 1,y = 0);
exgcd(b,a%b,y,x),y -= a/b*x;
}
int main()
{
freopen("division.in","r",stdin);
freopen("division.out","w",stdout);
ios::sync_with_stdio(0);
string S;int D;cin >> S >> D;
int n = S.size();S = " "+S;
int K = D,x,y,C = 1;
while (K%2 == 0) K /= 2,C *= 2;
while (K%5 == 0) K /= 5,C *= 5;
exgcd(10,K,x,y);pw[0] = 1;x = (x+K)%K;
for (int i = 1;i <= n;i++) pw[i] = (pw[i-1]*x)%K;
g[0] = B[0] = 1;
int sum = 0;
for (int i = 1;i <= n;i++)
{
if(i >= 20) F[H[i-20]] = mod(F[H[i-20]]+f[i-20]),G[H[i-20]] = mod(G[H[i-20]]+g[i-20]),sum = mod(sum+g[i-20]);
h[i] = (h[i-1]*10+S[i]-'0')%D,B[i] = B[i-1]*10%D,H[i] = (h[i]*pw[i])%K;
for (int j = i;j >= max(1,i-18);j--)
{
if ((h[i]-h[j-1]*B[i-j+1])%D) f[i] = mod(f[i]+g[j-1]);
else g[i] = mod(g[i]+mod(f[j-1]+g[j-1]));
}
if (h[i]%C == 0) f[i] = mod(f[i]+mod(sum-G[H[i]])),g[i] = mod(g[i]+mod(F[H[i]]+G[H[i]]));
else f[i] = mod(f[i]+sum);
}
cout << mod(f[n]+g[n]) << '\n';
return 0;
}
C.矩阵删除
Sol1:
首先我们不考虑 “两个矩阵如果删除的元素位置不同,但最后得到的结果相同,我们认为是相同的” 这句话,可以得到一个朴素的 dp:\(f_{i,j}=\sum\limits_{j-k\leq l \leq j+k}f_{i-1,l}\),然后这个用前缀和优化转移即可做到 \(\mathcal O(nm)\)。
回过头来观察这句话对结果的影响,同一行一段相等的元素,移除它们的结果是一样的,这意味着我们会计算许多重复状态,考虑去除重复贡献。
我们发现对于第 \(i\) 行相邻的两个相同元素 \(j-1,j\),它们对应上一层的范围是这样的:

(红线为 \(j-1\),蓝线为 \(j\))
显然,上图中被白线框出来的线段被重复覆盖了,这一段为 \([j-k,j+k-1]\)。
我们新增一个数组 \(g\) 来记录每个元素可能会重复计算的贡献,那么 \(f\) 的转移方程就不难推出:
\[f_{i,j}=\sum\limits_{j-k\leq l \leq j+k}f_{i-1,l}-\sum\limits_{j-k+1\leq l \leq j+k}g_{i-1,l} \]注意 \(g\) 的起始位置为 \(j-k+1\),因为左端点不会产生重复贡献。
根据 \(g\) 数组的定义和我们上面推出的式子,可以得到转移:
\[g_{i,j}=[a_{i,j}=a_{i,j-1}]\times (\sum\limits_{j-k\leq l\leq j+k-1}f_{i-1,l}-\sum\limits_{j-k+1\leq l\leq j+k-1}g_{i-1,l}) \]答案即为 \(\sum\limits_{1\leq i\leq m} f_{n,i}-\sum\limits_{2\leq i\leq m} g_{n,i}\)。
然后这个也是从一段区间转移,前缀和优化即可,时间复杂度 \(\mathcal O(nm)\)。
Sol2:
若不考虑下一行,那么当前行一个连续段内每个位置都是等价的,唯一不同的是对下层决策区间的限制,而当前连续段对下层的决策区间是可以确定的,为 \([l-k,r+k]\),于是可以写出以下复杂度为 \(O(n^4)\) 的记搜:
点击查看代码
int D(int i,int l,int r)
{
if (i > n) return 1;
if (f[i].find(l*3000+r) != f[i].end()) return f[i][l*3000+r];
int res = 0;
for (int j = l;j <= r;j++)
{
int p = j;
while(p < r && a[i][p+1] == a[i][p]) p++;
res = mod(res+D(i+1,max(j-k,1),min(p+k,m))),j = p;
}
return f[i][l*3000+r] = res;
}
D.路径查询
首先对于询问我们可以发现最后的答案一定是形如下图:
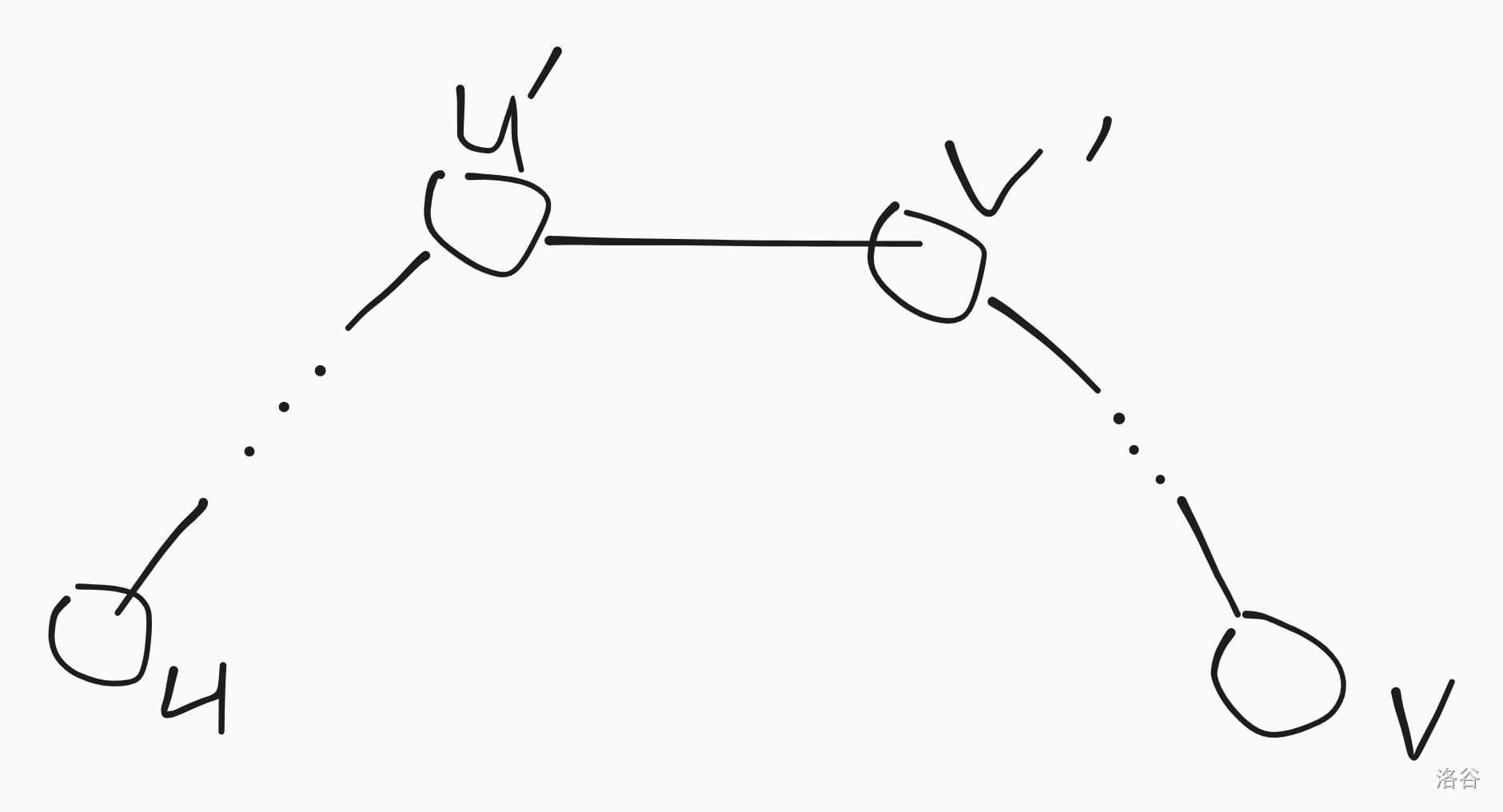
并且最大的边一定在左右两侧中的一侧。
那我们考虑 kruskal 从小到大加边,每次去合并连通块,因为我们是从小到大加的,所以最后答案一定会变成下图:

那么我们考虑合并的时候将出边和询问都合并到一个点上,使用启发式合并可以做到 \(O(n\log^2 n)\)。
标签:int,11.21,leq,times10,define,sum,mod From: https://www.cnblogs.com/ZepX-D/p/18561285