在现代项目管理中,任务分解是确保项目顺利进行的关键步骤。它不仅帮助团队明确目标,还能有效分配资源,提高工作效率。为了帮助项目经理和团队更好地进行任务分解,市场上涌现了许多优秀的项目管理工具。本文将为您推荐10款优质的任务分解工具,帮助您在项目管理中事半功倍。
禅道项目管理软件
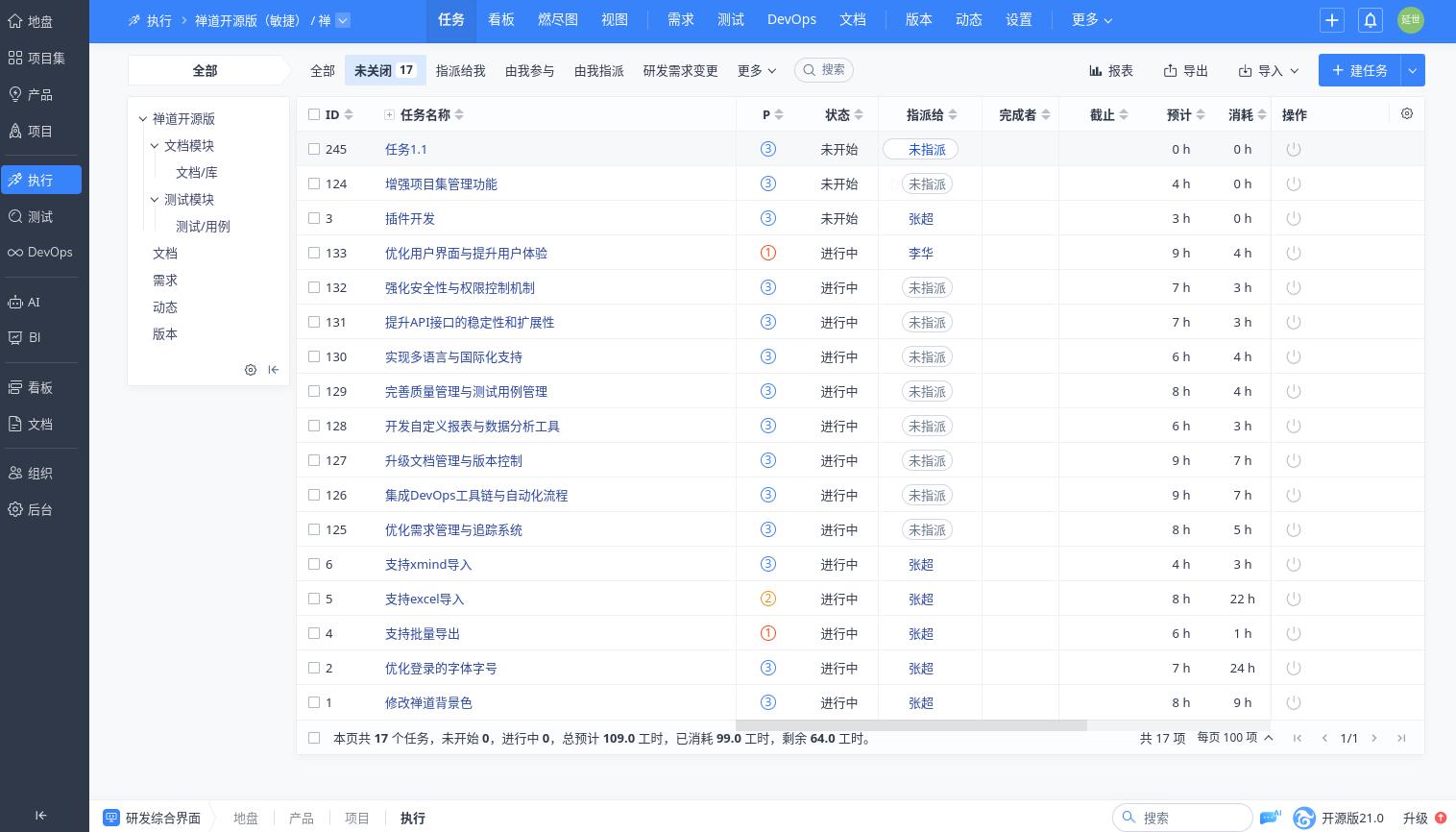
禅道项目管理软件是一款开源的项目管理工具,广泛应用于软件开发领域。它提供了从需求管理、任务分配到缺陷跟踪的全方位功能。禅道的任务分解功能尤为出色,支持多级任务分解,帮助团队将大项目拆解为可执行的小任务。此外,禅道还支持自定义工作流,适应不同项目的管理需求。对于需要高度定制化的项目团队来说,禅道是一个不可多得的选择。
禅道的界面简洁直观,易于上手。它不仅支持Web端使用,还提供了桌面客户端,方便团队成员随时随地进行任务管理。禅道的社区支持也非常强大,用户可以在社区中找到大量的插件和扩展,进一步增强软件的功能。总的来说,禅道项目管理软件是一款功能全面、易于使用的任务分解工具,适合各类项目团队使用。
Monday
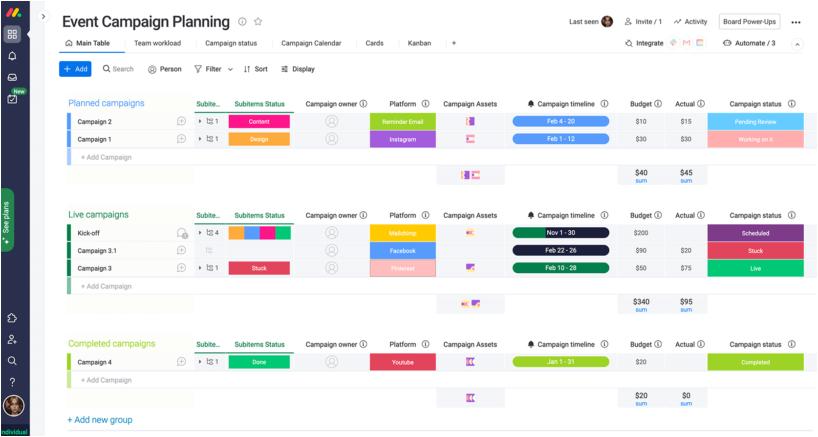
Monday是一款功能强大的在线项目管理工具,以其直观的界面和灵活的功能著称。它支持多种视图模式,包括看板、甘特图和日历视图,帮助团队从不同角度进行任务分解和跟踪。Monday的任务分解功能非常灵活,支持多级任务分解和子任务管理,确保每个任务都能被细化到可执行的程度。此外,Monday还支持自动化功能,可以自动触发任务状态更新和通知,减少手动操作的繁琐。
Monday的协作功能也非常出色,团队成员可以在同一个平台上进行实时沟通和协作。它还支持与其他常用工具的集成,如Slack、Google
Drive等,进一步提高工作效率。对于需要高度协作和灵活性的团队来说,Monday是一个理想的选择。它的用户界面设计非常友好,即使是新手也能快速上手。总的来说,Monday是一款功能强大、易于使用的任务分解工具,适合各类项目团队使用。
Planisware
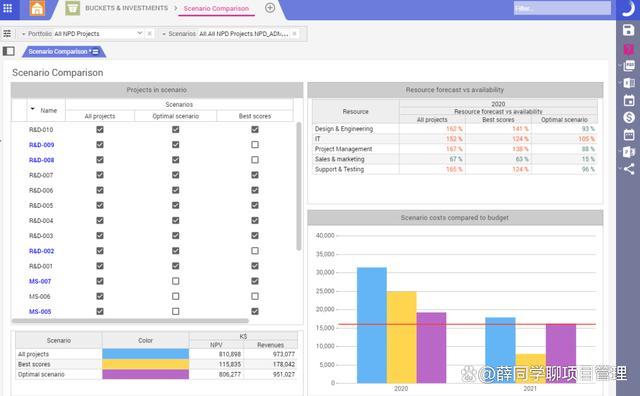
Planisware是一款专业的项目和产品组合管理软件,广泛应用于复杂项目管理领域。它提供了强大的任务分解功能,支持多级任务分解和子任务管理,帮助团队将复杂项目拆解为可执行的小任务。Planisware的任务分解功能不仅支持手动分解,还支持自动分解,根据项目需求自动生成任务树,大大提高了任务分解的效率。此外,Planisware还支持资源管理和风险管理,帮助团队更好地进行项目规划和执行。
Planisware的界面设计非常专业,功能强大,适合大型企业和复杂项目的管理。它支持多种视图模式,包括甘特图、网络图和资源视图,帮助团队从不同角度进行任务分解和跟踪。Planisware还支持与其他常用工具的集成,如Microsoft
Project、SAP等,进一步提高工作效率。对于需要高度专业化和复杂项目管理的团队来说,Planisware是一个不可多得的选择。总的来说,Planisware是一款功能强大、专业化的任务分解工具,适合大型企业和复杂项目团队使用。
Xebrio
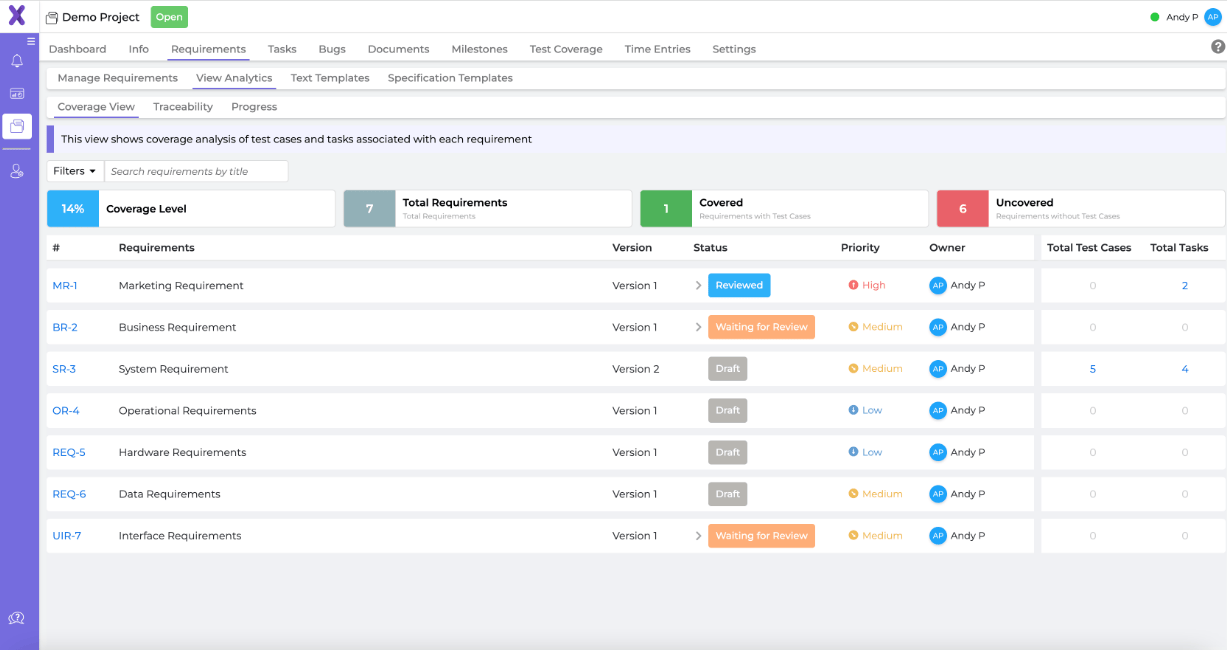
Xebrio是一款新兴的项目管理工具,以其创新的功能和灵活的界面著称。它提供了强大的任务分解功能,支持多级任务分解和子任务管理,帮助团队将复杂项目拆解为可执行的小任务。Xebrio的任务分解功能不仅支持手动分解,还支持自动分解,根据项目需求自动生成任务树,大大提高了任务分解的效率。此外,Xebrio还支持资源管理和风险管理,帮助团队更好地进行项目规划和执行。
Xebrio的界面设计非常现代化,功能强大,适合各类项目团队使用。它支持多种视图模式,包括看板、甘特图和日历视图,帮助团队从不同角度进行任务分解和跟踪。Xebrio还支持与其他常用工具的集成,如Slack、Google
Drive等,进一步提高工作效率。对于需要创新和灵活性的团队来说,Xebrio是一个理想的选择。它的用户界面设计非常友好,即使是新手也能快速上手。总的来说,Xebrio是一款功能强大、易于使用的任务分解工具,适合各类项目团队使用。
Plutio
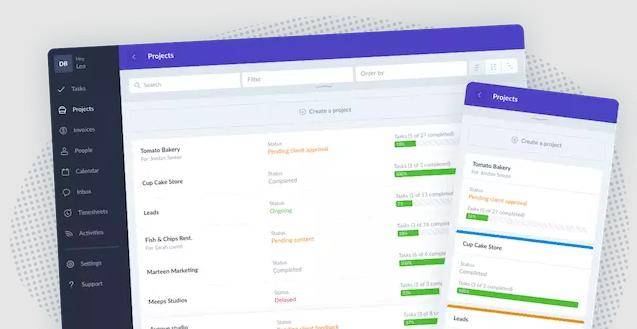
Plutio是一款综合性的项目管理和客户关系管理工具,广泛应用于自由职业者和中小型企业。它提供了强大的任务分解功能,支持多级任务分解和子任务管理,帮助团队将复杂项目拆解为可执行的小任务。Plutio的任务分解功能不仅支持手动分解,还支持自动分解,根据项目需求自动生成任务树,大大提高了任务分解的效率。此外,Plutio还支持资源管理和风险管理,帮助团队更好地进行项目规划和执行。
Plutio的界面设计非常简洁,功能强大,适合自由职业者和中小型企业使用。它支持多种视图模式,包括看板、甘特图和日历视图,帮助团队从不同角度进行任务分解和跟踪。Plutio还支持与其他常用工具的集成,如Slack、Google
Drive等,进一步提高工作效率。对于需要综合性和灵活性的团队来说,Plutio是一个理想的选择。它的用户界面设计非常友好,即使是新手也能快速上手。总的来说,Plutio是一款功能强大、易于使用的任务分解工具,适合自由职业者和中小型企业使用。
Basecamp
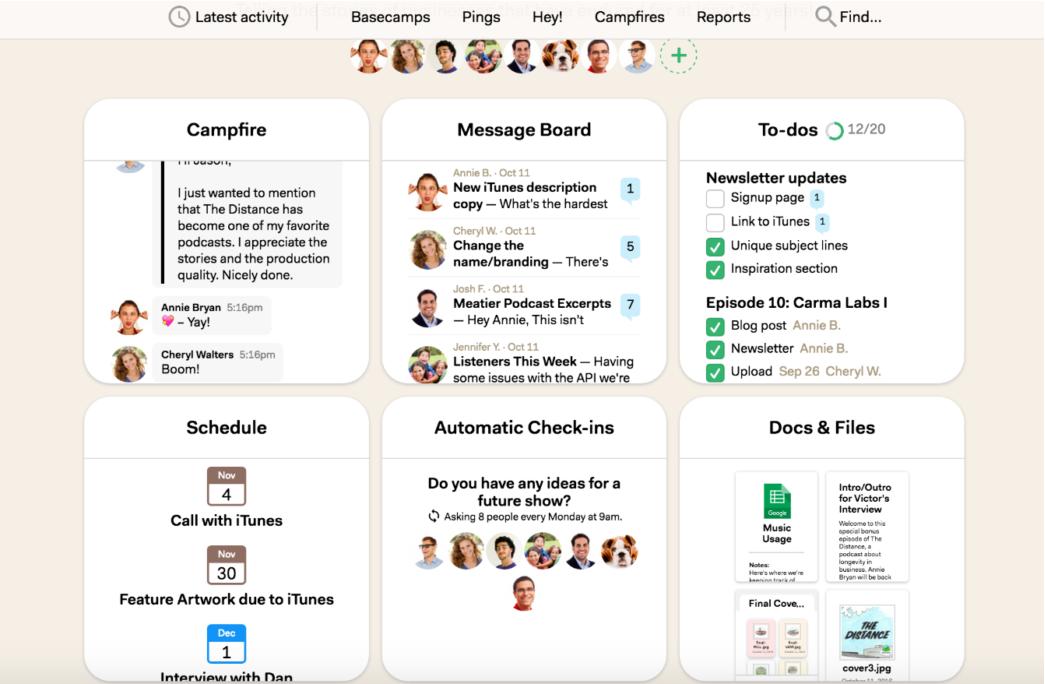
Basecamp是一款老牌的项目管理工具,以其简洁的界面和强大的功能著称。它提供了强大的任务分解功能,支持多级任务分解和子任务管理,帮助团队将复杂项目拆解为可执行的小任务。Basecamp的任务分解功能不仅支持手动分解,还支持自动分解,根据项目需求自动生成任务树,大大提高了任务分解的效率。此外,Basecamp还支持资源管理和风险管理,帮助团队更好地进行项目规划和执行。
Basecamp的界面设计非常简洁,功能强大,适合各类项目团队使用。它支持多种视图模式,包括看板、甘特图和日历视图,帮助团队从不同角度进行任务分解和跟踪。Basecamp还支持与其他常用工具的集成,如Slack、Google
Drive等,进一步提高工作效率。对于需要简洁和灵活性的团队来说,Basecamp是一个理想的选择。它的用户界面设计非常友好,即使是新手也能快速上手。总的来说,Basecamp是一款功能强大、易于使用的任务分解工具,适合各类项目团队使用。
Nifty
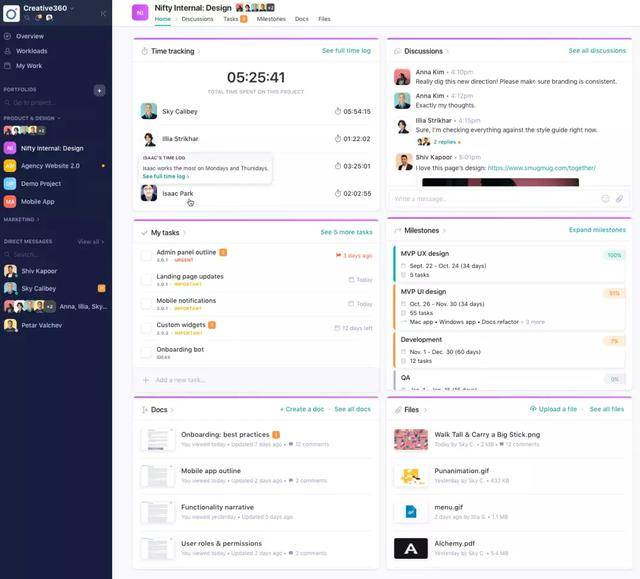
Nifty是一款新兴的项目管理工具,以其创新的功能和灵活的界面著称。它提供了强大的任务分解功能,支持多级任务分解和子任务管理,帮助团队将复杂项目拆解为可执行的小任务。Nifty的任务分解功能不仅支持手动分解,还支持自动分解,根据项目需求自动生成任务树,大大提高了任务分解的效率。此外,Nifty还支持资源管理和风险管理,帮助团队更好地进行项目规划和执行。
Nifty的界面设计非常现代化,功能强大,适合各类项目团队使用。它支持多种视图模式,包括看板、甘特图和日历视图,帮助团队从不同角度进行任务分解和跟踪。Nifty还支持与其他常用工具的集成,如Slack、Google
Drive等,进一步提高工作效率。对于需要创新和灵活性的团队来说,Nifty是一个理想的选择。它的用户界面设计非常友好,即使是新手也能快速上手。总的来说,Nifty是一款功能强大、易于使用的任务分解工具,适合各类项目团队使用。
nTask
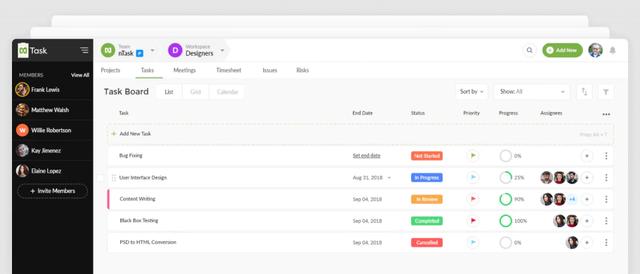
nTask是一款综合性的项目管理工具,广泛应用于中小型企业和团队。它提供了强大的任务分解功能,支持多级任务分解和子任务管理,帮助团队将复杂项目拆解为可执行的小任务。nTask的任务分解功能不仅支持手动分解,还支持自动分解,根据项目需求自动生成任务树,大大提高了任务分解的效率。此外,nTask还支持资源管理和风险管理,帮助团队更好地进行项目规划和执行。
nTask的界面设计非常简洁,功能强大,适合中小型企业和团队使用。它支持多种视图模式,包括看板、甘特图和日历视图,帮助团队从不同角度进行任务分解和跟踪。nTask还支持与其他常用工具的集成,如Slack、Google
Drive等,进一步提高工作效率。对于需要综合性和灵活性的团队来说,nTask是一个理想的选择。它的用户界面设计非常友好,即使是新手也能快速上手。总的来说,nTask是一款功能强大、易于使用的任务分解工具,适合中小型企业和团队使用。
GanttPRO
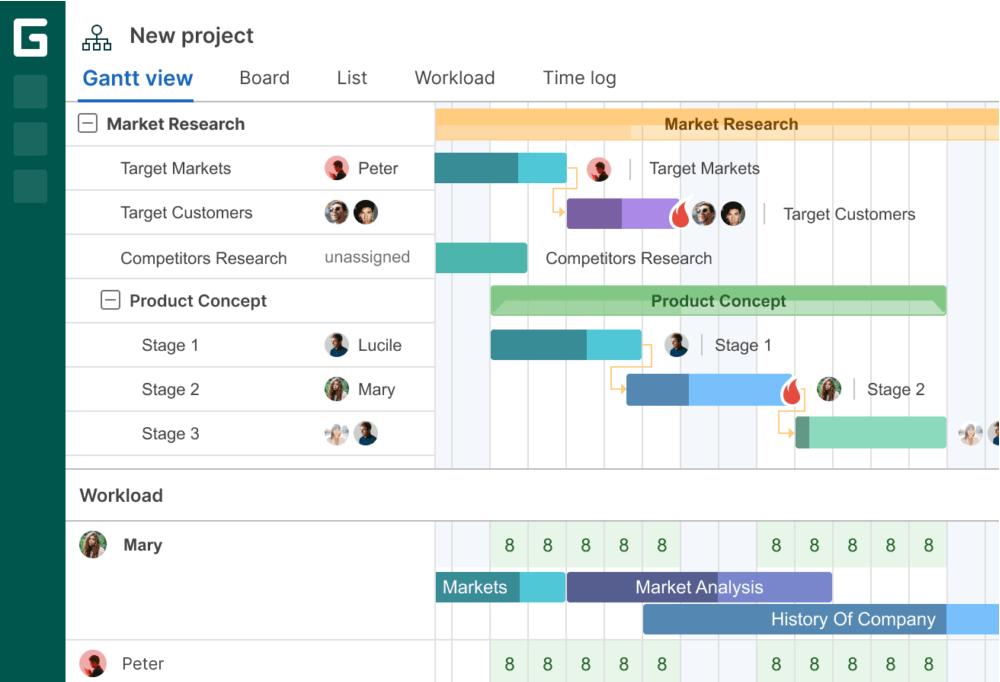
GanttPRO是一款专业的甘特图项目管理工具,广泛应用于复杂项目管理领域。它提供了强大的任务分解功能,支持多级任务分解和子任务管理,帮助团队将复杂项目拆解为可执行的小任务。GanttPRO的任务分解功能不仅支持手动分解,还支持自动分解,根据项目需求自动生成任务树,大大提高了任务分解的效率。此外,GanttPRO还支持资源管理和风险管理,帮助团队更好地进行项目规划和执行。
GanttPRO的界面设计非常专业,功能强大,适合大型企业和复杂项目的管理。它支持多种视图模式,包括甘特图、网络图和资源视图,帮助团队从不同角度进行任务分解和跟踪。GanttPRO还支持与其他常用工具的集成,如Microsoft
Project、SAP等,进一步提高工作效率。对于需要高度专业化和复杂项目管理的团队来说,GanttPRO是一个不可多得的选择。总的来说,GanttPRO是一款功能强大、专业化的任务分解工具,适合大型企业和复杂项目团队使用。
Visor
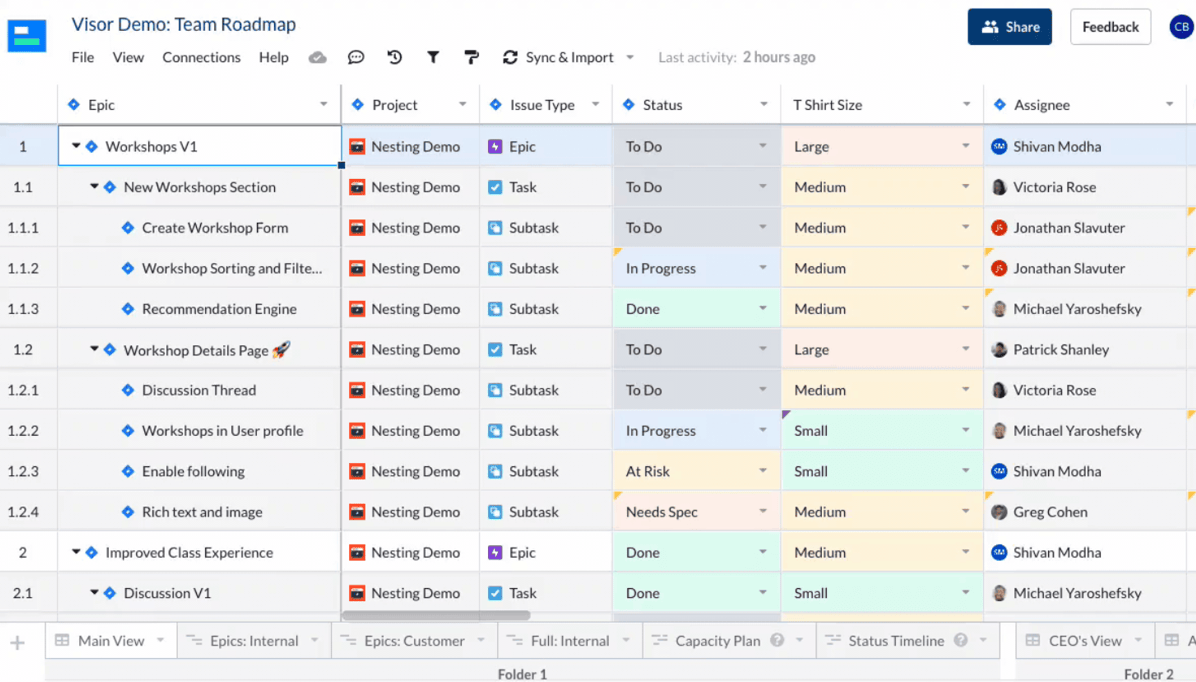
Visor是一款新兴的项目管理工具,以其创新的功能和灵活的界面著称。它提供了强大的任务分解功能,支持多级任务分解和子任务管理,帮助团队将复杂项目拆解为可执行的小任务。Visor的任务分解功能不仅支持手动分解,还支持自动分解,根据项目需求自动生成任务树,大大提高了任务分解的效率。此外,Visor还支持资源管理和风险管理,帮助团队更好地进行项目规划和执行。
Visor的界面设计非常现代化,功能强大,适合各类项目团队使用。它支持多种视图模式,包括看板、甘特图和日历视图,帮助团队从不同角度进行任务分解和跟踪。Visor还支持与其他常用工具的集成,如Slack、Google
Drive等,进一步提高工作效率。对于需要创新和灵活性的团队来说,Visor是一个理想的选择。它的用户界面设计非常友好,即使是新手也能快速上手。总的来说,Visor是一款功能强大、易于使用的任务分解工具,适合各类项目团队使用。
在选择任务分解工具时,项目团队应根据自身需求和项目特点进行选择。无论是需要高度定制化的禅道项目管理软件,还是追求简洁和灵活性的Basecamp,市场上都有适合的工具。通过合理选择和使用这些工具,项目团队可以更高效地进行任务分解,确保项目顺利进行。
FAQ
1. 如何选择适合自己团队的任务分解工具?
选择任务分解工具时,应考虑团队规模、项目复杂度、预算和团队成员的技能水平。对于小型团队,简洁易用的工具如Basecamp可能更合适;而对于大型复杂项目,专业化的工具如Planisware可能更为适合。
2. 任务分解工具是否支持与其他工具的集成?
大多数现代任务分解工具都支持与其他常用工具的集成,如Slack、Google Drive、Microsoft
Project等。在选择工具时,应确保其支持与团队常用工具的集成,以提高工作效率。
3. 如何评估任务分解工具的性能和效果?
评估任务分解工具的性能和效果可以通过试用期进行。大多数工具提供免费试用或演示版本,团队可以在试用期内评估工具的功能、易用性和性能,确保其满足项目需求。
标签:10,项目,项目管理,支持,神器,任务,分解,视图,团队 From: https://www.cnblogs.com/chanzhi/p/18586268