Gall 定律
一个有效的复杂系统通常是从一个有效的简单系统演化而来的
—— John Gall
本文将带你一步步探究 Transformer 模型中先进的位置编码技术。我们将通过迭代改进编码位置的方法,最终得出 旋转位置编码 (Rotary Postional Encoding, RoPE),这也是最新发布的 LLama 3.2 和大多数现代 transformer 模型所采用的方法。本文旨在尽量减少所需的数学知识,但理解一些基本的线性代数、三角学和自注意力机制是有帮助的。
问题陈述
你可以通过词语与其他词语的关系来理解一个词语的意义
—— John Rupert Firth
在所有问题中,首先要做的是理解 我们到底在解决什么问题。Transformer 中的自注意力机制用于理解序列中词元之间的关系。自注意力是一种 集合 操作,这意味着它是 排列等变的。如果我们不通过位置编码来丰富自注意力,许多重要的关系将 无法被确定。
下面通过一个例子更好的说明此问题。
引导示例
以下面这句话为例,单词的位置不同:
\[\text{The dog chased another dog} \]显然,“dog” 在两个位置上指代的是两个不同的实体。让我们看看如果我们首先对它们进行词元化,使用 Llama 3.2 1B 模型获得词元嵌入,并将它们传递给 torch.nn.MultiheadAttention 会发生什么。
import torch
import torch.nn as nn
from transformers import AutoTokenizer, AutoModel
model_id = "meta-llama/Llama-3.2-1B"
tok = AutoTokenizer.from_pretrained(model_id)
model = AutoModel.from_pretrained(model_id)
text = "The dog chased another dog"
tokens = tok(text, return_tensors="pt")["input_ids"]
embeddings = model.embed_tokens(tokens)
hdim = embeddings.shape[-1]
W_q = nn.Linear(hdim, hdim, bias=False)
W_k = nn.Linear(hdim, hdim, bias=False)
W_v = nn.Linear(hdim, hdim, bias=False)
mha = nn.MultiheadAttention(embed_dim=hdim, num_heads=4, batch_first=True)
with torch.no_grad():
for param in mha.parameters():
nn.init.normal_(param, std=0.1) # Initialize weights to be non-negligible
output, _ = mha(W_q(embeddings), W_k(embeddings), W_v(embeddings))
dog1_out = output[0, 2]
dog2_out = output[0, 5]
print(f"Dog output identical?: {torch.allclose(dog1_out, dog2_out, atol=1e-6)}") #True
如我们所见,如果没有任何位置编码,那么经过多头自注意力操作后, 同一个词元在不同位置的输出是相同的,尽管这些词元代表的是不同的实体。接下来,我们将开始设计一种增强自注意力位置编码的方法,使其能够根据位置来区分单词之间的关系。
理想的位置编码方案应该如何表现?
理想属性
让我们尝试定义一些理想的属性,使优化过程尽可能简单。
属性 1 - 每个位置的唯一编码 (跨序列)
每个位置都需要一个唯一的编码,无论序列长度如何,该编码保持一致 - 位置 5 的词元应该具有相同的编码,无论当前序列的长度是 10 还是 10,000。
属性 2 - 两个编码位置之间的线性关系
位置之间的关系应该是数学上简单的。如果我们知道位置 \(p\) 的编码,那么计算位置 \(p+k\) 的编码应该很简单,使模型更容易学习位置模式。
如果你考虑我们在数轴上如何表示数字,很容易理解 5 离 3 有 2 步之遥,或者 10 离 15 有 5 步之遥。相同的直观关系应该存在于我们的编码中。
属性 3 - 泛化到比训练中遇到的序列更长的序列
为了增加模型在现实世界的实用性,它们应该能够泛化到训练分布之外。因此,我们的编码方案需要足够灵活,以适应非预期的输入长度,而不会违反任何其他理想属性。
属性 4 - 由模型可以学习的确定性过程生成
如果我们的位置编码可以从确定性过程中得出,那将是理想的。这将使模型更有效地学习我们编码方案背后的机制。
属性 5 - 可扩展到多个维度
随着多模态模型的普及,我们的位置编码方案能够自然地从 \(1D\) 扩展到\(nD\) 至关重要。这将使模型能够处理图像、脑部扫描等二维和四维数据。
现在我们知道了理想的属性 (以下称为 \(Pr_n\)),让我们开始设计和迭代我们的编码方案。
整数位置编码
第一个可能的方案是简单地将词元的位置整数值添加到每个词元嵌入的分量中,值的范围从 \(0 \rightarrow L\),其中 \(L\) 是当前序列的长度。

在上面的动画中,我们利用索引值为 \(\color{#699C52}\text{chased}\) 词元创建了位置编码向量并将其添加到词元嵌入中。这里的嵌入值是 Llama 3.2 1B 中的真实值的一个子集。我们可以观察到它们集中在 0 附近。这是希望避免训练过程中的 梯度消失或梯度爆炸 问题,因此我们希望在模型中保持这一点。
很明显,我们当前的简单方法会带来问题。位置值的大小远大于输入的实际值。这意味着信噪比非常低,模型很难将语义信息与位置编码区分开。
有了这个新的认识,一个自然的后续步骤是通过 \(\frac{1}{N}\) 来规范化位置值。这样将值限制在 0 到 1 之间,但引入了另一个问题。如果我们选择 \(N\) 为当前序列的长度,那么位置值在不同长度的序列中会完全不同,从而违反了 \(Pr_1\)。
是否有更好的方法确保我们的数字在 0 到 1 之间?如果我们仔细思考一下,可能会想到从十进制转到二进制数。
二进制位置编码
与其将 (可能已经规范化的) 整数位置添加到每个词元的嵌入分量中,我们不如将位置转换成二进制表示,并将其 拉伸 以匹配我们的嵌入维度,如下所示。

我们已经将感兴趣的位置信息 (252) 转换为其二进制表示 (11111100),并将每一位加到词元嵌入的相应分量中。最低有效位 (LSB) 将在每个后续词元中在 0 和 1 之间循环,而最高有效位 (MSB) 将在每 \(2^{n-1}\) 个词元中循环,其中 \(n\) 是位数。你可以在下面的动画中看到不同索引的二进制位置编码向量 \([^1]\)。
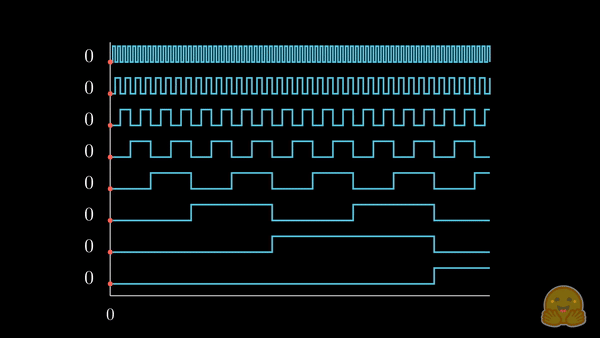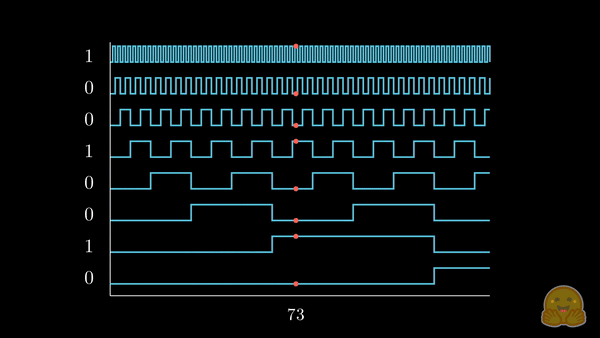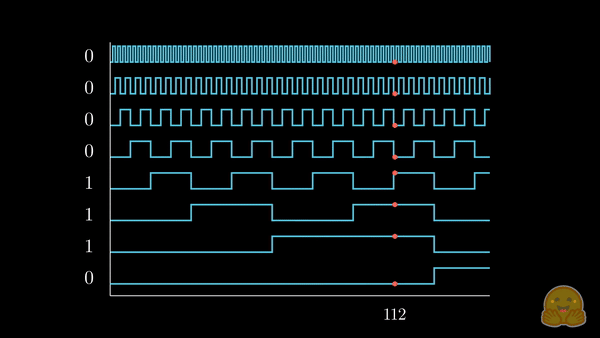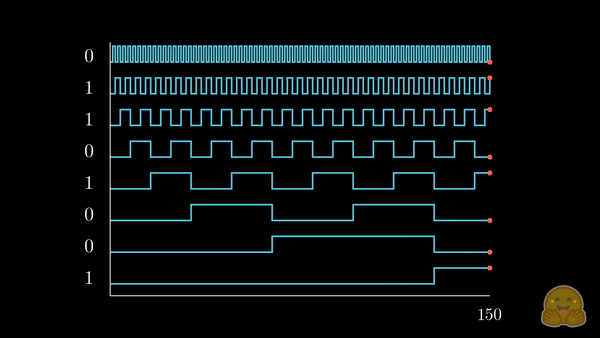
我们解决了值域的问题,并获得了在不同序列长度下都一致的唯一编码。如果我们绘制一个低维的嵌入表示,并观察对不同值加入二进制位置向量后的变化,会发生什么呢?
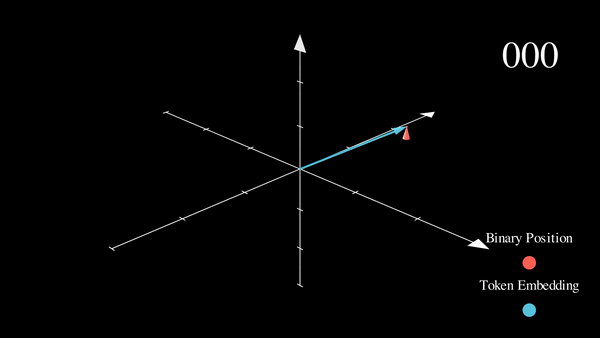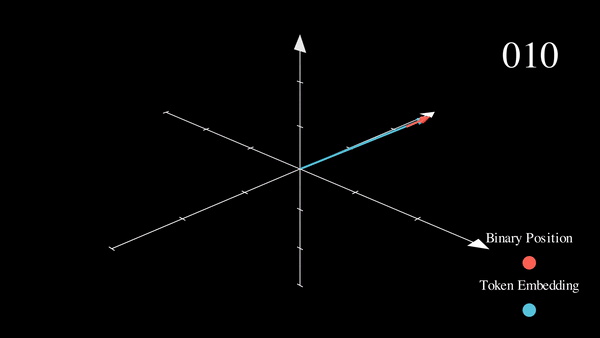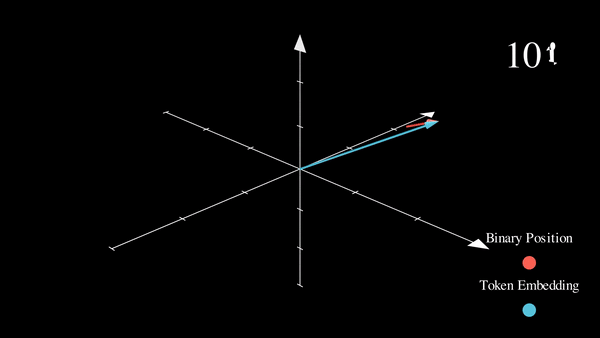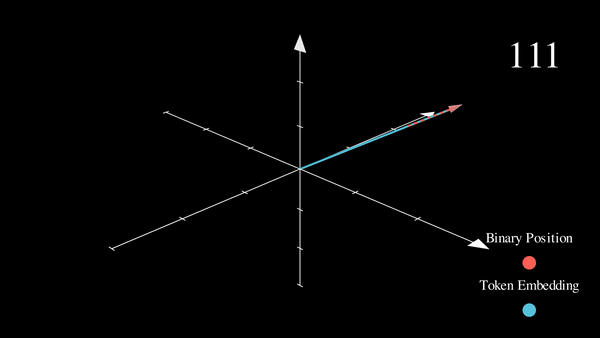
我们可以看到,结果非常“跳跃”(这符合二进制离散性的预期)。优化过程更喜欢平滑、连续和可预测的变化。我们是否知道哪些函数的具有与此类似的值域,同时也是平滑和连续的?
稍作思考就会发现,\(\sin\) 和 \(\cos\) 恰好符合这个需求!
正弦位置编码
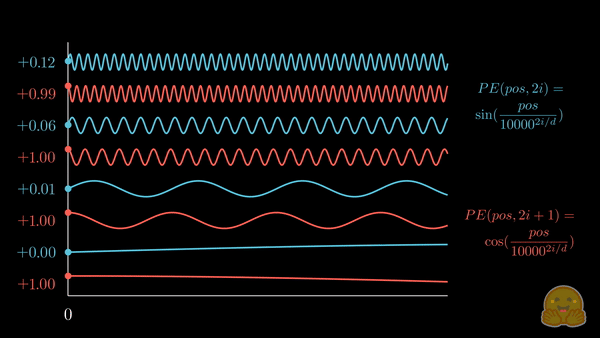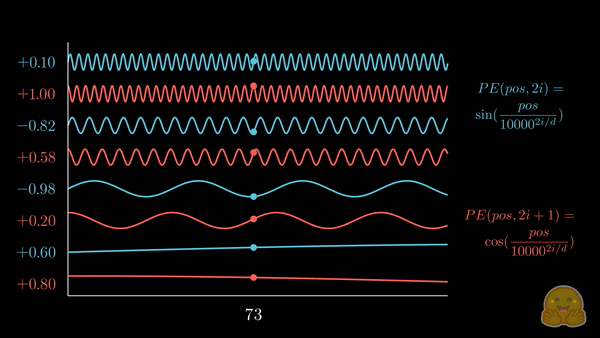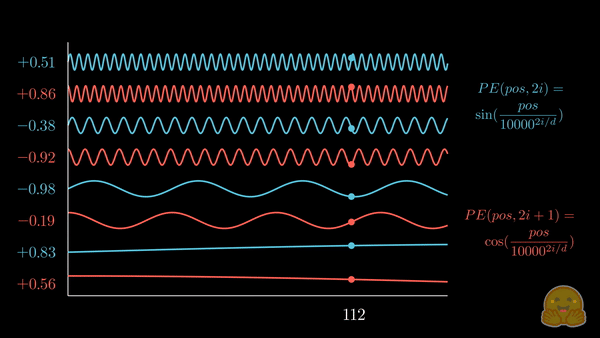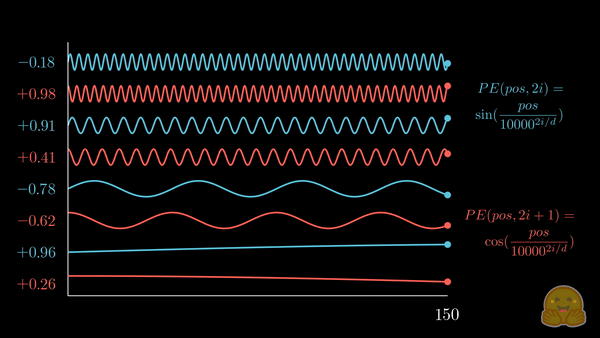
上面的动画展示了位置嵌入的可视化,其中每个分量交替来自 \(\sin\) 和 \(\cos\),并逐步增加其波长。如果将其与前一个动画对比,你会注意到惊人的相似性!
我们现在得到了 正弦嵌入,其最初在 Attention is all you need 论文中被提出。以下是相关公式:
\[PE_{(pos,2i)} = \color{#58C4DD}\sin\left(\color{black}\frac{pos}{10000^{2i/d}}\color{#58C4DD}\right)\color{black} \\ \quad \\ PE_{(pos,2i+1)} = \color{#FC6255}\cos\left(\color{black}\frac{pos}{10000^{2i/d}}\color{#FC6255}\right)\color{black} \\ \]其中,\(pos\) 是词元的位置索引,\(i\) 是位置编码向量的分量索引,\(d\) 是模型的维度,\(10,000\) 是 基波长 (以下简称为 \(\theta\)),它根据分量索引被拉伸或压缩。你可以代入一些实际的值,直观地感受这种几何级数的变化。
乍看之下,这些公式中有些部分可能会让人困惑。例如,作者为什么选择 \(10,000\)?为什么我们要对偶数和奇数位置分别使用 \(\sin\) 和 \(\cos\)?
选择 \(10,000\) 作为基准波长似乎是通过实验确定的 \([^2]\)。解读同时使用 \(\sin\) 和 \(\cos\) 的意义较为复杂,但对于我们逐步理解问题的方法却至关重要。关键在于,我们希望两个位置编码 \(Pr_2\) 之间具有线性关系。要理解使用 \(\sin\) 和 \(\cos\) 如何联合产生这种线性关系,我们需要深入了解一些三角学知识。
假设一个正弦和余弦组成的序列对,每个序列对对应一个频率 \(\omega_i\)。我们的目标是找到一个线性变换矩阵 \(\mathbf{M}\),该矩阵可以将这些正弦函数按照固定偏移量 \(k\) 进行平移:
\[\mathbf{M} \cdot \begin{bmatrix} \sin(\omega_i p) \\ \cos(\omega_i p) \end{bmatrix} = \begin{bmatrix} \sin(\omega_i(p + k)) \\ \cos(\omega_i(p + k)) \end{bmatrix} \]这些频率 \(\omega_i\) 遵循随维度索引 \(i\) 减小的几何级数,其定义为:
\[\omega_i = \frac{1}{10000^{2i/d}} \]为了找到这个变换矩阵,我们可以将其表示为一个通用的 2×2 矩阵,其系数为未知数 \(u_1\)、\(v_1\)、\(u_2\) 和 \(v_2\):
\[\begin{bmatrix} u_1 & v_1 \\ u_2 & v_2 \end{bmatrix} \cdot \begin{bmatrix} \sin(\omega_i p) \\ \cos(\omega_i p) \end{bmatrix} = \begin{bmatrix} \sin(\omega_i(p+k)) \\ \cos(\omega_i(p+k)) \end{bmatrix} \]通过对右侧应用三角函数的加法公式,我们可以将其展开为:
\[\begin{bmatrix} u_1 & v_1 \\ u_2 & v_2 \end{bmatrix} \cdot \begin{bmatrix} \sin(\omega_i p) \\ \cos(\omega_i p) \end{bmatrix} = \begin{bmatrix} \sin(\omega_i p)\cos(\omega_i k) + \cos(\omega_i p)\sin(\omega_i k) \\ \cos(\omega_i p)\cos(\omega_i k) - \sin(\omega_i p)\sin(\omega_i k) \end{bmatrix} \]通过匹配系数,我们可以得到一组方程:
\[\begin{align*} u_1\sin(\omega_i p) + v_1\cos(\omega_i p) &= \cos(\omega_i k)\sin(\omega_i p) + \sin(\omega_i k)\cos(\omega_i p) \\ u_2\sin(\omega_i p) + v_2\cos(\omega_i p) &= -\sin(\omega_i k)\sin(\omega_i p) + \cos(\omega_i k)\cos(\omega_i p) \end{align*} \]通过比较 \(\sin(\omega_i p)\) 和 \(\cos(\omega_i p)\) 的系数,我们可以解出未知系数:
\[\begin{align*} u_1 &= \cos(\omega_i k) & v_1 &= \sin(\omega_i k) \\ u_2 &= -\sin(\omega_i k) & v_2 &= \cos(\omega_i k) \end{align*} \]最终得到的变换矩阵 \(\mathbf{M_k}\) 为:
\[\mathbf{M_k} = \begin{bmatrix} \cos(\omega_i k) & \sin(\omega_i k) \\ -\sin(\omega_i k) & \cos(\omega_i k) \end{bmatrix} \]如果你曾从事过游戏编程,可能会觉得这个结果似曾相识。没错,这就是 旋转矩阵! \([^3]\)。
因此,Noam Shazeer 在 Attention is all you need 一文中设计的编码方案早在 2017 年就已经通过旋转来编码相对位置了!但从正弦位置编码到 RoPE (旋转位置编码) 却花了整整 4 年,尽管旋转的概念早已被提出……
绝对位置编码 vs 相对位置编码
认识到旋转的重要性后,让我们回到引导示例,并尝试为下一次迭代探索一些灵感。
\[\begin{align*} &\hspace{0.7em}0 \hspace{1.4em} 1 \hspace{2em} 2 \hspace{2.6em} 3 \hspace{2.4em} 4\\ &\text{The dog chased another dog} \\ \\ &\hspace{0.3em}\text{-2} \hspace{1.4em} \text{-1} \hspace{1.7em} 0 \hspace{2.6em} 1 \hspace{2.4em} 2\\ &\text{The dog chased another dog} \end{align*} \]上图展示了词元的绝对位置以及从 \(\text{chased}\) 到其他词元的相对位置。通过正弦位置编码,我们生成了一个表示绝对位置的独立向量,并利用一些三角技巧将相对位置编码了进来。
当我们试图理解这些句子时, this 单词是这篇博客中第 2157 个词的重要性有多大?或者我们更关心它与周围单词的关系?单词的绝对位置对于其意义来说很少重要——真正重要的是单词之间的相互关系。
在上下文中理解位置编码
从现在开始,我们需要将位置编码放在 自注意力机制的上下文中 中分析。再强调一次,自注意力机制让模型能够评估输入序列中不同元素的重要性,并动态调整它们对输出的影响。
\[\text{Attn}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V \]在之前的所有迭代中,我们生成了一个独立的位置信息向量,并在 \(Q\)、\(K\) 和 \(V\) 投影之前将其 加到 词元嵌入上。这样做实际上是将位置信息与语义信息混合在一起,对嵌入向量的范数进行了修改。为了避免污染语义信息,我们应该尝试使用乘法进行编码。
用词典的类比来说,当我们查找一个单词 (query) 在词典 (keys) 中的含义时,邻近的单词应该比远处的单词有更大的影响。这种影响是通过 \(QK^T\) 的点积来决定的,因此位置编码应该集中在这里!
\[\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta \]点积的几何解释为我们提供了一个极好的灵感: 我们可以通过改变两个向量之间的角度来调整点积的结果。此外,通过旋转向量,我们不会改变向量的范数,从而不会影响词元的语义信息。
现在,我们知道应该把注意力放在哪里,并从另一个视角看到了为什么旋转是一种合理的“通道”来编码位置信息——让我们把一切整合起来吧!
旋转位置编码 (RoPE)
旋转位置编码 (Rotary Positional Encoding,简称 RoPE ) 是在 RoFormer 论文 中定义的 (Jianlin Su在他的博客 这里 和 这里中独立设计了这一方法)。
如果直接跳到最终结果,可能会觉得它像是某种“魔法”。但通过将正弦位置编码放在自注意力 (尤其是点积) 的背景下思考,我们可以看出它的核心逻辑。
与正弦位置编码类似,我们将向量 \(\mathbf{q}\) 或 \(\mathbf{k}\) (而非投影前的 \(\mathbf{x}\)) 分解为二维的对/块。不同于通过将基于逐渐减小频率的正弦函数生成的向量相加来直接编码 绝对 位置,RoPE 通过 对每一对分量应用旋转矩阵 来编码 相对 位置。
令 \(\mathbf{q}\) 或 \(\mathbf{k}\) 为位置 \(p\) 处的输入向量。我们创建一个块对角矩阵,其中 \(\mathbf{M_i}\) 是对应分量对的旋转矩阵:
\[R(\mathbf{q}, p) = \begin{pmatrix} \mathbf{M_1} & & & \\ & \mathbf{M_2} & & \\ & & \ddots & \\ & & & \mathbf{M_{d/2}} \end{pmatrix} \begin{pmatrix} q_1 \\ q_2 \\ \vdots \\ q_d \end{pmatrix} \]与正弦位置编码类似,\(\mathbf{M_i}\) 的定义如下:
\[\mathbf{M_i} = \begin{bmatrix} \cos(\omega_i p) & \sin(\omega_i p) \\ -\sin(\omega_i p) & \cos(\omega_i p) \end{bmatrix} \]
实际上,我们并不直接通过矩阵乘法计算 RoPE,因为使用稀疏矩阵会导致计算效率低下。取而代之,我们可以利用计算规律直接对分量对分别应用旋转操作:
\[R_{\Theta,p}^d q = \begin{pmatrix} q_1 \\ q_2 \\ q_3 \\ q_4 \\ \vdots \\ q_{d-1} \\ q_d \end{pmatrix} \otimes \begin{pmatrix} \cos p\theta_1 \\ \cos p\theta_1 \\ \cos p\theta_2 \\ \cos p\theta_2 \\ \vdots \\ \cos p\theta_{d/2} \\ \cos p\theta_{d/2} \end{pmatrix} + \begin{pmatrix} -q_2 \\ q_1 \\ -q_4 \\ q_3 \\ \vdots \\ -q_d \\ q_{d-1} \end{pmatrix} \otimes \begin{pmatrix} \sin p\theta_1 \\ \sin p\theta_1 \\ \sin p\theta_2 \\ \sin p\theta_2 \\ \vdots \\ \sin p\theta_{d/2} \\ \sin p\theta_{d/2} \end{pmatrix} \]就是这么简单!通过在 \(\mathbf{q}\) 和 \(\mathbf{k}\) 的二维块上巧妙地应用旋转操作,并从加法切换为乘法,我们可以显著提升评估性能 \([^4]\)。
将 RoPE 扩展到 \(n\)- 维
我们已经探讨了 RoPE 的 \(1D\) 情况,到这里为止,我希望你已经对这种直观上难以理解的 Transformer 组件有了一定的认识。接下来,我们来看看如何将其扩展到更高维度的数据,例如图像。
一个直观的想法是直接使用图像的 $ \begin{bmatrix} x \ y \end{bmatrix}$ 坐标对。这看起来很合理,毕竟我们之前就是随意地将分量配对。然而,这将是一个错误!
在 \(1D\) 情况下,我们通过对输入向量中分量对的旋转来编码相对位置 \(m - n\)。对于 \(2D\) 数据,我们需要独立地编码水平和垂直的相对位置 (例如 \(m - n\) 和 \(i - j\))。RoPE 的精妙之处在于其如何处理多维度。与其尝试在单次旋转中编码所有位置信息,不如在 同一维度内配对分量并旋转,否则我们会混淆 \(x\) 和 \(y\) 偏移信息。通过分别处理每个维度,我们保持了数据的自然结构。这一方法可以推广到任意多维数据!
位置编码的未来
RoPE 是位置编码的最终形式吗?DeepMind 的 这篇论文 深入分析了 RoPE 并指出了一些根本性问题。总结: RoPE 并非完美解决方案,模型主要专注于低频分量,而对某些低频分量的旋转能够提升 Gemma 2B 的性能!
未来可能会有一些突破,或许从信号处理中汲取灵感,例如小波或分层实现。随着模型越来越多地被量化以便于部署,我也期待在低精度计算下仍然保持鲁棒性的编码方案出现。
结论
在 Transformer 中,位置编码常被视为事后的补丁。我认为我们应当改变这种看法——自注意力机制有一个“致命弱点”,它需要被反复修补。
希望这篇博客能让你明白,即便这种方法起初看起来难以直观理解,你也可以发现最新的状态 -of-the-art 位置编码。在后续文章中,我将探讨如何实践 RoPE 的具体实现细节以优化性能。
这篇文章最初发布在 这里
参考文献
- Transformer Architecture: The Positional Encoding
- Rotary Embeddings: A Relative Revolution
- How positional encoding works in transformers?
- Attention Is All You Need
- Round and round we go! What makes Rotary Positional Encodings useful?
- RoFormer: Enhanced Transformer with Rotary Position Embedding
\([^1]\): 正弦和二进制动画来源于 视频。
\([^2]\): 使用 \(\theta = 10000\) 可生成 \(2 \pi \cdot 10000\) 个唯一位置,理论上下文长度上限约为 63,000。
\([^3]\): 本文部分内容参考自 这篇精彩的文章 (作者: Amirhossein Kazemnejad。
\([^4]\): 相关实验数据请参见 EleutherAI 的这篇文章。)
标签:编码,cos,位置,bmatrix,设计,omega,sin From: https://www.cnblogs.com/huggingface/p/18585176原文链接: https://hf.co/blog/designing-positional-encoding
原文作者: Christopher Fleetwood
译者: chenin-wang