斜率优化
\(y=kx+b\) 形式维护队列,询问不单调则二分决策点。
Slope Trick
如果决策函数满足以下条件:
- 连续
- 凸包,每一段斜率为整数
- 凸包上断点之间的一次函数斜率总和为 \(\mathcal O(n)\) 级别
则称这个函数满足性质 \(T\),且如果 \(f,h\) 都满足性质 \(T\),则 \(f+h\) 也满足性质 \(T\)。
于是对于这种函数,维护凸包开头一次函数的 \(k,b\) 和后面斜率转折点,其中斜率在转折点增加多少就插入几个转折点。
于是我们可以快速维护这个决策函数:
- \(f'=f+g\):将两函数的转折点集合合并。
- \(f'(x)=\min\limits_{t\le x}/\max\limits_{t\le x} f_t\):令 \(k=0\) 时左右两边断点为 \(\ell,r\),维护 \(\le \ell\) 和 \(r\le\) 的断点集合 \(\mathcal L,\mathcal R\),两个操作分别对应去掉一个集合。
- \(f'(x)=f(x+t)\):打标记,实现平移。
习题
- CF713C
- 严格递增转不减之后,可写出转移方程 \(f(i,j)=\min\limits_{k\le i} f(k,j-1)+|a_i-j|\),随便维护。
- ABC217H
- 首先此题有明显的定义域,初始为 \([0,0]\),于是将 \((0,0)\) 两边的斜率设为 \(>n\),可以保证不会影响到答案。
- 其次有 \(f'(i)=\min\limits_{|i-j|\le 1} f(j)\) 的操作,等价于 \(\mathcal L\) 左平移 \(1\) 单位,\(\mathcal R\) 右平移 \(1\) 单位,打个标记即可实现。
- 其余两个操作相当于加类似
\_和_/的函数,讨论一下与 \(\ell, r\) 的关系并处理断点应放入的集合就好。
- ARC070C
- 与上一题很类似,只不过加的是绝对值函数,其实更好处理了。
- P3642
- 首先考虑将每个节点的函数值包含其父边,方便处理。
- 然后令父边权值为 \(w\),这个函数转移类似于 \(f'(x)=\min\limits_{0\le t}f(x-t)+|w-t|\),定义域的限制使转移比较复杂,根据分讨之后发现凸函数的变化如下所示:
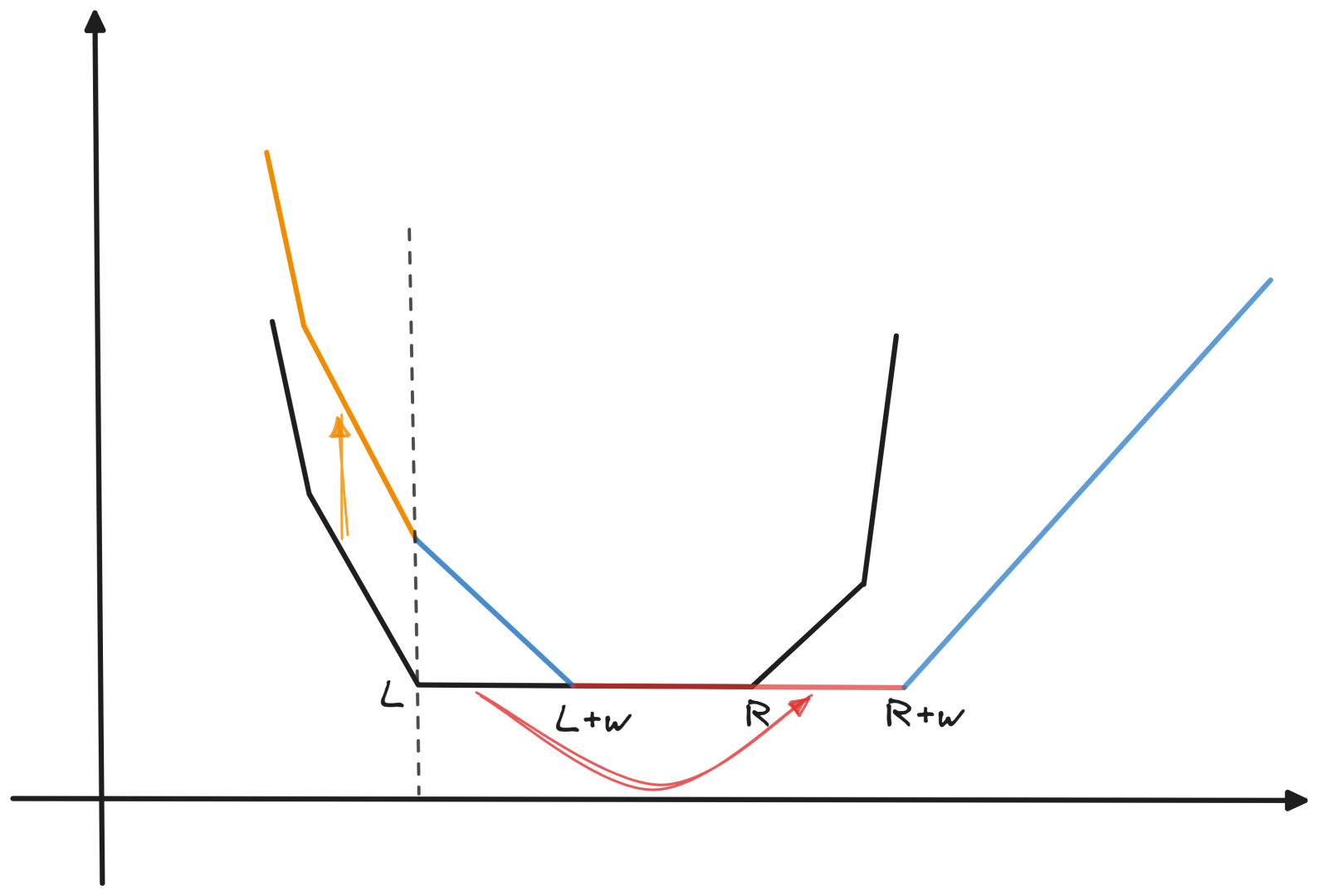
- 本质就是先保留 \(\mathcal R\) 的一个元素,之后并将 \(\ell,r\) 加 \(w\),使用左偏树即可。
wqs 二分
咕一会儿。
https://www.luogu.com/article/pf2lj18t
闵可夫斯基和
https://www.cnblogs.com/apjifengc/p/17041194.html
标签:le,修缮,limits,凸性,斜率,mathcal,断点,dp,函数 From: https://www.cnblogs.com/notears/p/18540734