图论系列:
前言:
咲いた野の花よ
ああどうか教えておくれ
人は何故傷つけあって
争うのでしょう
相关题单:
一.并查集
1.基础定义与操作
(1)定义
并查集是一种用于管理元素所属集合的数据结构,实现为一个森林,其中每棵树表示一个集合,树中的节点表示对应集合中的元素。
(2)操作
合并(merge):合并两个元素所属集合(合并对应的树)
查询(find):查询某个元素所属集合(查询对应的树的根节点),这可以用于判断两个元素是否属于同一集合
并查集在经过修改后可以支持单个元素的删除、移动;使用动态开点线段树还可以实现可持久化并查集。
2.算法流程:
在并查集中,我们将一个个元素看成一个个点,将逻辑所属关系转化为图上的连通性问题。
(1)初始化
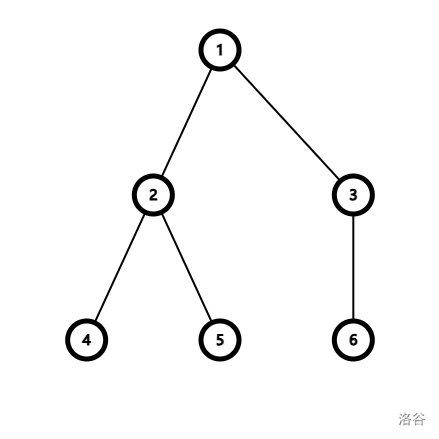
一开始每一个元素都属于一个单独的集合,将元素看作点,相当于现在有很多个只有根节点的树。方便起见,我们将根节点的父亲设为自己。(如图)

代码:
for(int i=1;i<=n;i++) fa[i]=i;
(2)查询
查询很简单,由于我们记录了每个点的父亲节点(而根节点的父亲就是自己),那么我们就一直跳父亲直到跳到一个点满足 \(fa_x=x\)。
如图,对于点 5 ,\(fa_5=2\) ,于是跳到点 2,\(fa_2=1\),于是跳到点 1,\(fa_1=1\),满足 \(fa_x=x\) 的要求,于是点 5 就属于 1 所在的这个集合。
代码:
inline int find(int x)
{
if(x!=fa[x]) return find(fa[x]);//当前不是根节点就跳根节点
return fa[x];//说明是根节点了,x=fa[x],返回的实际上就是根节点
}
(3)合并
对于两个点 \(x,y\),我们现在需要合并其所在的两个集合。由于每个点所在的集合实际上是由点所在树的根决定的,如果 \(root_x=root_y\),那么就说明 \(x,y\) 已经在同一个集合内了,反之两点不在一个集合,此时只需将其中一个点的根的父亲设为另一个点的根,即 \(fa_{root_x}=root_y\) 。
这个时候我们再去判断原本属于 \(root_x\) 所在的集合的点,它们肯定都会先跳到 \(root_x\),而此时 $fa_{root_x}=y $,于是这些点的根就成功的转化为了 \(root_y\) ,原本 \(root_y\) 所在的点的根自然也是 \(root_y\) ,于是就完成了合并。
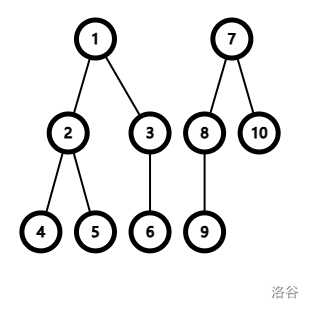
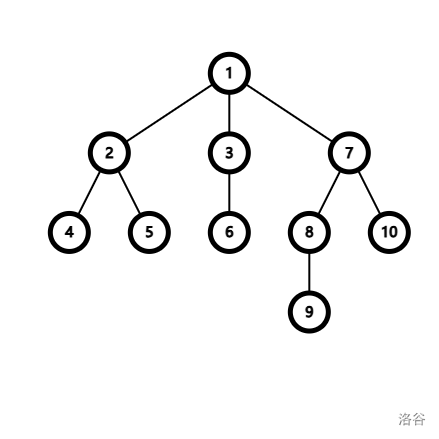
如上图,现在我们要合并 5 所在的集合与 9 所在的集合。首先找到经过跳父亲找到 \(root_5=1,root_9=7\),然后再把 \(fa_7\) 改为 \(1\),相当于就是连了一条 \(1 \to 7\) 的无向边,于是两个集合就成功合并了。(如下图)
代码:
inline void merge(int x,int y)
{
x=find(x),y=find(y);//找到两点的根节点
if(x==y) return ;//如果已经在一个集合内了就不管
fa[x]=y;//否则将其中一个根节点的父亲设为另一个点的根节点
}
(4)路径压缩
但是暴力跳父亲明显存在一定的问题,比如对于一条长为 \(n\) 的链,如果查询链尾的根节点,那么要跳 \(n\) 次,这样时间复杂度极高。
考虑优化。首先对于从链尾到根节点路径上经过的所有点,肯定都是属于根节点代表的这个集合内的,那么每次跳父亲也太费劲了。在查询的过程中,由于需要一层一层的跳父亲,于是通过递归,找到根节点之后,将路径上所有点的父亲都设为根节点,这样以后查询就只需要跳一次了。
优化过后的并查集时间复杂度是反阿克曼函数,将当作一个较小的常数即可。

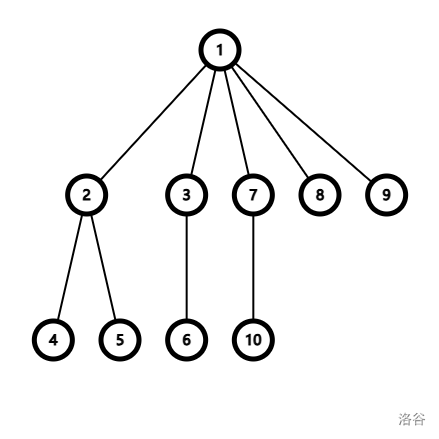
如上图,现在我们用路径压缩来查询 9 节点的根节点,跳父亲就是 \(9 \to 8 \to 7 \to 1\),然后递归回来就是 \(fa_7=fa_8=fa_9=1\)。(如下图)
代码:
inline int find(int x)
{
if(x!=fa[x]) fa[x]=find(fa[x]);
return fa[x];//如果当前是根节点,那么返回的就是根节点,如果不是(因为上面那句没有加 return ),所以路径上的所有点都会遍历这一句,此时fa[x]都被修改为根节点了,所以返回的还是根节点
}
(5)启发式合并
由于得知了并查集找根的实质与路径压缩的优化过程,所以对于一个集合代表的树,树高越小时间复杂度自然越小。对于两个集合,那么元素个数小的集合合并到元素个数大的集合时间复杂度会更优(学术上有证明,真的跑的很快,后面会介绍树上启发式合并)。
代码:
//查询的代码不变,多维护一个siz数组
inline void merge(int x,int y)
{
x=find(x),y=find(y);
if(x==y) return ;
if(siz[x]>siz[y]) swap(x,y);
fa[x]=y,siz[y]+=siz[x];//保证是小集合合并到大集合,同时记录当前集合的大小
}
for(int i=1;i<=n;i++) fa[i]=i,siz[i]=1;//初始化每个集合大小为1
(6)删除
这个很牛啊,想了很久,结果有板子题。
对于删除单点 \(x\),我们想到的第一个方法肯定是把 \(x\) 的父亲指向自己。但是这样会把 \(x\) 的下属也跟着脱离出来,这明显错了。
既然直接改变 \(x\) 点的父亲行不通,那把原先的 \(x\) 点留在那儿,成为一个虚点。然后我们再建立一个新的点 \(y\) 成为真正的 \(x\) 点,这样 \(x\) 的下属找祖宗的时候就可以正常经过虚点,但我们实际的 \(x\) 却在 \(y\)。
但是这里又产生了第二个问题:我怎么才能知道真正的 \(x\) 点在哪?
当然在 \(y\) 啦,记录一下每个点真实所在下标即可。对于一个 \(fa\) 数组, \(fa_{1 \sim n}\) 存真实点的下标,而真实点从 \(n+1\) 开始用(相当于我们钦定点 \(1\) 真实在 \(n+1\),点 \(n\) 真实在 \(2n\))。
于是初始化的时候 \(fa_i=n+i , 1 \leq i \leq n\),\(fa_i=i,n+1 \leq i \leq 2*n+q\)(第二个式子是因为真实点的 \(fa_i=i\),而操作最多 \(q\) 次,最多会用到 \(2*n+q\) 个点)。
那么删除的时候就非常简单了,初始化 \(num=2*n\),表示当前用到哪个点了。那么删除一个点 \(x\) 时,只用将 \(fa_x=++num\) 即可。
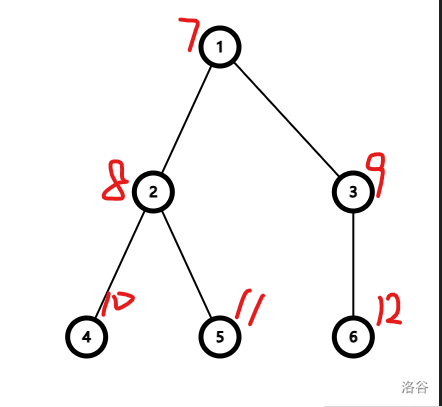
可能有点抽象,画图理解,对于上图删去点 2(红色值表示的就是 \(fa_i\) 的值,此时 \(num=12\)),\(fa_2=13\) (\(x\) 表示当前这里是个虚点)。此时查询点 4,它还是在集合 1 中。(如下图)
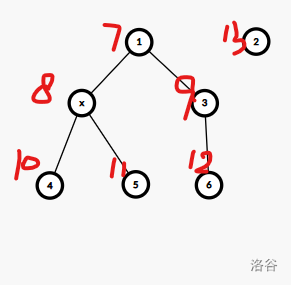
除了初始化,其余操作代码均不变。
(7)移动
将某个元素移动到另一个集合去。显然的,删了以后再加不久行了。
(8)带权/拓展域
带权并查集,这个在例题里结合来讲可能会清晰一点。
3.应用
我觉得 oi wiki 的专题已经比较全面了,其他的可能结合后面的题加深对一些并查集套路的理解。
https://oi-wiki.org/topic/dsu-app/
二.最小生成树
这里讨论的都是无向图连通图内的最小生成树,有向图最小生成树是最小树形图,以后可能会写吧。
1.相关定义
生成树:对于连通图,形态是一棵树的生成子图称为生成树。(所以生成树是一颗连通了图上所有点的树。非连通图不存在生成树。)
生成森林:由每个连通分量的生成树组成的子图称为 生成森林。
非树边:对于某棵生成树,原图的不在生成树上的边称为非树边。
给定一张带权连通图,求其边权和最小的生成树,称为 最小生成树(Minimum Spanning Tree,MST)。对于非连通图,对每个连通分量求最小生成树即得最小生成森林。
2.算法
最小生成树常见有三种(Kruskal,Prim与Boruvka)求法,其实只用学 Kruskal 与 Boruvka 就可以了(毕竟 Kruskal 后面有 Kruskal 重构树,Boruvka 可以解决一些特殊图)。
理解 Kruskal 实际上就是按边权大小从小到大排序之后,使用并查集维护当前边连接的两点是否已经在同一个集合内了,如果在就跳过,不在就加入这条边,然后在并查集中将这两点合并起来。
(我好懒啊,其实算法挺简单的,oiwiki 这部分写的挺全面的 https://oi-wiki.org/graph/mst/)
练习题: