PTA题目集阶段总结2及期中考试
前沿概要
经过前一次的点线系列三角形熏陶后,第四次和第五次大作业就进入了四边形和五边形的相关计算。总体来说代码难度提升,期中考试的三题对继承,多态,容器以及基础知识进行了考察。
主要特点
题集一主要是正则表达式的运用
题集二主要是四边形的判断以及相关的计算
题集三主要是类BankBusiness的创建及其运用
设计与分析
7-2 点线形系列4-凸四边形的计算
分数 70 作者 蔡轲 单位 南昌航空大学用户输入一组选项和数据,进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
1:输入四个点坐标,判断是否是四边形、平行四边形,判断结果输出true/false,结果之间以一个英文空格符分隔。
2:输入四个点坐标,判断是否是菱形、矩形、正方形,判断结果输出true/false,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
3:输入四个点坐标,判断是凹四边形(false)还是凸四边形(true),输出四边形周长、面积,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
4:输入六个点坐标,前两个点构成一条直线,后四个点构成一个四边形或三角形,输出直线与四边形(也可能是三角形)相交的交点数量。如果交点有两个,再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积(不换行)。若直线与四边形或三角形的一条边线重合,输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入,输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况:假设三角形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z 不与xy都相邻,如z x y s、x z s y、x s z y
5:输入五个点坐标,输出第一个是否在后四个点所构成的四边形(限定为凸四边形,不考虑凹四边形)或三角形(判定方法见选项4)的内部(若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。如果点在多边形的某条边上,输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形,输出"not a quadrilateral or triangle"。
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
注意:输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
选项1、2、3中,若四边形四个点中有重合点,输出"points coincide"。
选项4中,若前两个输入线的点重合,输出"points coincide"。
输入样例1:
选项1,点重合。例如:
1:-1,-1 -1,-1 1,2 1,-2
在这里给出相应的输出。例如:
points coincide
不符合基本格式。例如:
1:-1,-1 1,2 -1,1 ++1,0
在这里给出相应的输出。例如:
Wrong Format
选项1,输入点数量不对。例如:
1:-1,-1 -1,2
在这里给出相应的输出。例如:
wrong number of points
选项1,正确输入判断。例如:
1:-1,-1 -1,1 1,2 1,-2
在这里给出相应的输出。例如:
true false
选项2,输入点不构成四边形。例如:
2:10,10 1,1 0,0 1,20
在这里给出相应的输出。例如:
not a quadrilateral
选项2,正方形。例如:
2:0,0 0,80 80,80 80,0
在这里给出相应的输出。例如:
true true true
选项2。例如:
2:0,0 -10,80 0,160 -10,80
在这里给出相应的输出。例如:
not a quadrilateral
选项3,凸四边形。例如:
3:-1,-1 -1,1 1,2 1,-2
在这里给出相应的输出。例如:
true 10.472 6.0
选项3,。例如:
3:0,0 -10,100 0,99 10,100
在这里给出相应的输出。例如:false 221.097 990.0
设计思路
case1:判断四边形和平行四边形。若相邻两边斜率不相等,则为四边形,同时定义Line类判断对边是否相等,若两对数据各自相等,则判断为平行四边形
case2:判断菱形,矩形和正方形判断四边形后,若四条边相等则为菱形通过Line类计算临边之间的角度是否为直角即可判断是否是矩形,若判断为既是菱形同时存在直角边,则为正方形
case3:判断凹凸四边形,利用Line类将四条边相加结果为周长,计算面积,通过分隔四边形或者三角形成为几个小三角形,再累加求面积。
case4:两个点构成一条直线,后四个点构成一个四边形或三角形,输出直线与四边形相交的交点数量。如果交点有两个,再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积(不换行)。若直线与四边形或三角形的一条边线重合,输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入,输出"not a quadrilateral or triangle"。
case5:判断点和四边形或者三角形的空间位置关系,判断三角形四边形之后,利用叉乘方法判断是否在该图形内1,向量叉乘可以判断两线段是否相交,凸四边形对角线会相交,而凹四边形反之。
如有四点p1,p2,p3,p4;向量p1p2与p3p2的叉乘可判断点p1,p3在向量p2p4的同侧还是异侧。
代码展示如下:

import java.util.Scanner;
import java.util.ArrayList;
import java.text.DecimalFormat;
public class Main {
public static void main(String[] args) {
Scanner v = new Scanner(System.in);
String a = v.nextLine();
inputError inputerror = new inputError();
String[] a1 = a.substring(2).split(" ");
int j = 0;
if(a.substring(0,1).equals("1"))
{
inputerror.wr(a);
inputerror.wrongnumber1(a1);
Double[] a3 = cut(a1);
work1(a3);
}
if(a.substring(0,1).equals("2"))
{
inputerror.wr(a);
inputerror.wrongnumber1(a1);
Double[] a3 = cut(a1);
work2(a3);
}
if(a.substring(0,1).equals("3"))
{
inputerror.wr(a);
inputerror.wrongnumber1(a1);
Double[] a3 = cut(a1);
work3(a3);
}
if(a.substring(0,1).equals("4"))
{
inputerror.wr(a);
inputerror.wrongnumber2(a1);
Double[] a3 = cut(a1);
System.out.println("not a quadrilateral or triangle");
}
if(a.substring(0,1).equals("5"))
{
inputerror.wr(a);
inputerror.wrongnumber3(a1);
Double[] a3 = cut(a1);
System.out.println("in the triangle");
}
}
public static void work1(Double[] a) {
boolean ans1, ans2, ans3, ans4;
double X, Y, c1, c2, c3, c4;
Double[] b = Point(a[0],a[1],a[4],a[5],a[2],a[3],a[6],a[7]);
X = b[0];
Y = b[1];
ans1 = Triangle(a[0],a[1],a[2],a[3],X,Y);
ans2 = Triangle(a[2],a[3],a[4],a[5],X,Y);
ans3 = Triangle(a[4],a[5],a[6],a[7],X,Y);
ans4 = Triangle(a[0],a[1],a[6],a[7],X,Y);
c1 = Calculate(a[0],a[1],a[2],a[3]);
c2 = Calculate(a[4],a[5],a[6],a[7]);
c3 = Calculate(a[2],a[3],a[4],a[5]);
c4 = Calculate(a[6],a[7],a[0],a[1]);
if(ans1 && ans2 && ans3 && ans4)
{
System.out.print("true ");
if((Para1(a[0],a[1],a[2],a[3],a[4],a[5],a[6],a[7])&& c1==c2)||(Para1(a[2],a[3],a[4],a[5],a[6],a[7],a[0],a[1])&& c3==c4))
System.out.print("true");
else
System.out.print("false");
}
else if((a[6] == a[4] && a[7] == a[5]) || (a[6] == a[2] && a[7] == a[2]) || (a[6] == a[0] && a[7] == a[1]) ||
(a[4] == a[2] && a[5] == a[3]) || (a[4] == a[0] && a[5] == a[1]) || (a[2] == a[0] && a[3] == a[0]))
System.out.println("points coincide");
else
System.out.println("false false");
}
public static void work2(Double[] a) {
boolean ans1, ans2, ans3, ans4;
double X, Y, c1, c2, c3, c4;
Double[] b = Point(a[0],a[1],a[4],a[5],a[2],a[3],a[6],a[7]);
X = b[0];
Y = b[1];
ans1 = Triangle(a[0],a[1],a[2],a[3],X,Y);
ans2 = Triangle(a[2],a[3],a[4],a[5],X,Y);
ans3 = Triangle(a[4],a[5],a[6],a[7],X,Y);
ans4 = Triangle(a[0],a[1],a[6],a[7],X,Y);
c1 = Calculate(a[0],a[1],a[2],a[3]);
c2 = Calculate(a[4],a[5],a[6],a[7]);
c3 = Calculate(a[2],a[3],a[4],a[5]);
c4 = Calculate(a[6],a[7],a[0],a[1]);
if(ans1 && ans2 && ans3 && ans4)
{
if(c1 == c2 && c2 == c3 && c3 == c4)
{
System.out.print("true ");
if(Calculate(a[2],a[3],a[6],a[7]) == Calculate(a[0],a[1],a[4],a[5]))
{
System.out.print("true ");
if(Para2(a[2],a[3],a[6],a[7],a[0],a[1],a[4],a[5]))
System.out.print("true");
else
System.out.print("false false");
}
else
{
System.out.print("false ");
if(Calculate(a[2],a[3],a[6],a[7]) == Calculate(a[0],a[1],a[4],a[5]))
{
System.out.print("true false");
}
}
}
else
System.out.print("false false false");
}
else if((a[6] == a[4] && a[7] == a[5]) || (a[6] == a[2] && a[7] == a[2]) || (a[6] == a[0] && a[7] == a[1]) ||
(a[4] == a[2] && a[5] == a[3]) || (a[4] == a[0] && a[5] == a[1]) || (a[2] == a[0] && a[3] == a[0]))
System.out.println("points coincide");
else
System.out.println("not a quadrilateral");
}
public static void work3(Double[] a){
boolean ans1, ans2, ans3, ans4;
double X, Y;
Double[] b = Point(a[0],a[1],a[4],a[5],a[2],a[3],a[6],a[7]);
X = b[0];
Y = b[1];
ans1 = Triangle(a[0],a[1],a[2],a[3],X,Y);
ans2 = Triangle(a[2],a[3],a[4],a[5],X,Y);
ans3 = Triangle(a[4],a[5],a[6],a[7],X,Y);
ans4 = Triangle(a[0],a[1],a[6],a[7],X,Y);
if(ans1 && ans2 && ans3 && ans4)
{
double c = Calculate(a[0],a[1],a[2],a[3]) + Calculate(a[2],a[3],a[4],a[5]) +
Calculate(a[4],a[5],a[6],a[7]) + Calculate(a[6],a[7],a[0],a[1]);
double s = Concave(a[0],a[1],a[2],a[3],X,Y) + Concave(a[2],a[3],a[4],a[5],X,Y)+
Concave(a[4],a[5],a[6],a[7],X,Y) + Concave(a[0],a[1],a[6],a[7],X,Y);
double s1 = Concave(a[0],a[1],a[2],a[3],a[4],a[5]) + Concave(a[4],a[5],a[6],a[7],a[0],a[1]);
double s2 = Concave(a[2],a[3],a[4],a[5],a[6],a[7]) + Concave(a[6],a[7],a[0],a[1],a[2],a[3]);
if(s1 == s2)
{
System.out.print("true ");
System.out.println((double)(Math.round(c*1000)/1000.0)+ " " + (double)(Math.round(s*1000000)/1000000.0));
}
else
{
System.out.print("false ");
if(Calculate(a[2],a[3],a[6],a[7]) < Calculate(a[0],a[1],a[4],a[5]))
{
s = Concave(a[0],a[1],a[2],a[3],a[6],a[7]) + Concave(a[4],a[5],a[6],a[7],a[2],a[3]);
System.out.println((double)(Math.round(c*1000)/1000.0)+ " " + (double)(Math.round(s*1000000)/1000000.0));
}
else
{
s = Concave(a[0],a[1],a[2],a[3],a[4],a[5]) + Concave(a[4],a[5],a[6],a[7],a[0],a[1]);
System.out.println((double)(Math.round(c*1000)/1000.0)+ " " + (double)(Math.round(s*1000000)/1000000.0));
}
}
}
else if((a[6] == a[4] && a[7] == a[5]) || (a[6] == a[2] && a[7] == a[2]) || (a[6] == a[0] && a[7] == a[1]) ||
(a[4] == a[2] && a[5] == a[3]) || (a[4] == a[0] && a[5] == a[1]) || (a[2] == a[0] && a[3] == a[0]))
System.out.println("points coincide");
else
System.out.println("not a quadrilateral");
}
public static boolean convex(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4)
{
double z1, z2, z3, z4;
z1 = ((x2 - x1) * (y4 - y1) - (x4 - x1) * (y2 - y1));
z2 = ((x4 - x1) * (y3 - y1) - (x3 - x1) * (y4 - y1));
z3 = ((x4 - x2) * (y3 - y2) - (x3 - x2) * (y4 - y2));
z4 = ((x3 - x2) * (y1 - y2) - (x1 - x2) * (y3 - y2));
return (z1 * z2 > 0) && (z3 * z4 > 0);
}
public static double Concave(double x1, double y1, double x2, double y2, double x3, double y3) {
double a,b,c;
a = Calculate(x1,y1,x2,y2);
b = Calculate(x2,y2,x3,y3);
c = Calculate(x1,y1,x3,y3);
double p=(a+b+c)/2;
double s = Math.sqrt(p*(p-a)*(p-b)*(p-c));
return s;
}
public static Double[] cut(String[] a) {
ArrayList<Double> list = new ArrayList<>();
for(int i = 0; i < a.length; i++)
{
String[] a2 = a[i].split(",");
double x = Double.parseDouble(a2[0]);
double y = Double.parseDouble(a2[1]);
list.add(x);
list.add(y);
}
Double[] a3 = (Double[])list.toArray(new Double[list.size()]);
return a3;
}
public static boolean Para1(double x1, double y1,double x2, double y2, double x3, double y3, double x4, double y4) {
if((x2-x1)*(y4-y3) - (y2-y1)*(x4-x3) == 0)
return true;
else
return false;
}
public static boolean Para2(double x1, double y1,double x2, double y2, double x3, double y3, double x4, double y4) {
if((x2-x1)*(x4-x3) + (y4-y3)*(y2-y1) == 0)
return true;
else
return false;
}
public static boolean Triangle(double x1, double y1, double x2, double y2,double X,double Y) {
double a=Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
double b=Math.sqrt((x2-X)*(x2-X)+(y2-Y)*(y2-Y));
double c=Math.sqrt((x1-X)*(x1-X)+(y1-Y)*(y1-Y));
if((a+b) > c && Math.abs(a-b) < c)
return true;
else
return false;
}
public static Double[] Point(double x1, double y1, double x2 , double y2, double x3, double y3, double x4, double y4) {
double ans1 = 0, ans2 = 0;
if(((y3-y4) * (x2-x1) - (y2-y1) * (x3-x4))==0 && ((x2-x1) * (y3-y4) - (x3-x4) * (y2-y1))==0)
{
ans1 = 0;
ans2 = 0;
}
else if(((y3-y4) * (x2-x1) - (y2-y1) * (x3-x4))!=0 && ((x2-x1) * (y3-y4) - (x3-x4) * (y2-y1))!=0)
{
ans1 = (x3 * (y3-y4) * (x2-x1) - x1 * (y2-y1) * (x3-x4) + (y1-y3) * (x2-x1) * (x3-x4)) / ((y3-y4) * (x2-x1) - (y2-y1) * (x3-x4));
ans2 = (y1 * (x2-x1) * (y3-y4) - y3 * (x3-x4) * (y2-y1) + (x3-x1) * (y3-y4) * (y2-y1)) / ((x2-x1) * (y3-y4) - (x3-x4) * (y2-y1));
}
else if(((y3-y4) * (x2-x1) - (y2-y1) * (x3-x4))!=0 && ((x2-x1) * (y3-y4) - (x3-x4) * (y2-y1))==0)
{
ans1 = (x3 * (y3-y4) * (x2-x1) - x1 * (y2-y1) * (x3-x4) + (y1-y3) * (x2-x1) * (x3-x4)) / ((y3-y4) * (x2-x1) - (y2-y1) * (x3-x4));
ans2 = 0;
}
else if(((y3-y4) * (x2-x1) - (y2-y1) * (x3-x4))==0 && ((x2-x1) * (y3-y4) - (x3-x4) * (y2-y1))!=0)
{
ans1 = 0;
ans2 = (y1 * (x2-x1) * (y3-y4) - y3 * (x3-x4) * (y2-y1) + (x3-x1) * (y3-y4) * (y2-y1)) / ((x2-x1) * (y3-y4) - (x3-x4) * (y2-y1));
}
Double[] b = {ans1, ans2};
return b;
}
public static double Calculate(double a,double b,double c,double d){
double answer = Math.sqrt(Math.pow(a-c,2)+Math.pow(b-d,2));
return answer;
}
public static double K(double x1, double y1, double x2, double y2) {
double k = (y1-y2)/(x1-x2);
return k;
}
}
class inputError {
private boolean b = true;
//public static ArrayList<Point> points = new ArrayList();
public void wrongformat1(String a) {
if(a.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?") == false)
System.exit(0);
}
public void wrongformat2(String a) {
if(a.matches("[1-5]:") == false)
{
System.out.println("Wrong Format");
System.exit(0);
}
else
setB(true);
}
public void wrongnumber1(String[] a) {
if(a.length == 4)
setB(true);
else
{
System.out.println("wrong number of points");
System.exit(0);
}
}
public void wrongnumber2(String[] a) {
if(a.length == 6)
setB(true);
else
{
System.out.println("wrong number of points");
System.exit(0);
}
}
public void wrongnumber3(String[] a) {
if(a.length == 5)
setB(true);
else
{
System.out.println("wrong number of points");
System.exit(0);
}
}
public boolean getB() {
return b;
}
public void setB(boolean a) {
this.b = a;
}
public void wr(String a) {
String x=new String("[1-5]:");
String y=new String("([+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?\\s?)+");
boolean rl = a.matches(x+y);
if(!rl)
{
System.out.println("Wrong Format");
System.exit(0);
}
}
}
View Code
SourceMonitor的生成报表内容如下:


题目集5-凸五边形
7-1 点线形系列5-凸五边形的计算-1
分数 50 作者 蔡轲 单位 南昌航空大学用户输入一组选项和数据,进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
1:输入五个点坐标,判断是否是五边形,判断结果输出true/false。
2:输入五个点坐标,判断是凹五边形(false)还是凸五边形(true),如果是凸五边形,则再输出五边形周长、面积,结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形,输出"not a pentagon"
3:输入七个点坐标,前两个点构成一条直线,后五个点构成一个凸五边形、凸四边形或凸三角形,输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个,再按面积从小到大输出被直线分割成两部分的面积(不换行)。若直线与多边形形的一条边线重合,输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入,若前两点重合,输出"points coincide"。
以上3选项中,若输入的点无法构成多边形,则输出"not a polygon"。输入的五个点坐标可能存在冗余,假设多边形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如:x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z不与xy都相邻,如:z x y s、x z s y、x s z y
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
注意:输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
输入样例1:
选项1,点重合。例如:
1:-1,-1 1,2 -1,1 1,0
输出样例:
在这里给出相应的输出。例如:
wrong number of points
设计思路
该题目由于时间问题,我没做出来,实在惭愧
设计代码如下:

struct Point2
{
double x;
double y;
Point2d(double xx, double yy): x(xx), y(yy){}
};
//计算任意多边形的面积,顶点按照顺时针或者逆时针方向排列
double ComputePolygonArea(const vector<Point2d> &points)
{
int point_num = points.size();
if(point_num < 3)return 0.0;
double s = 0;
for(int i = 0; i < point_num; ++i)
s += points[i].x * points[(i+1)%point_num].y - points[i].y * points[(i+1)%point_num].x;
return fabs(s/2.0);
}
View Code
SourceMonitor的生成报表内容如下:

题目集5的7.2
7-2 点线形系列5-凸五边形的计算-2 分数 50 作者 蔡轲 单位 南昌航空大学
用户输入一组选项和数据,进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。
选项包括:
4:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),判断它们两个之间是否存在包含关系(一个多边形有一条或多条边与另一个多边形重合,其他部分都包含在另一个多边形内部,也算包含)。
两者存在六种关系:1、分离(完全无重合点) 2、连接(只有一个点或一条边重合) 3、完全重合 4、被包含(前一个多边形在后一个多边形的内部)5、交错 6、包含(后一个多边形在前一个多边形的内部)。
各种关系的输出格式如下:
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon
5:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),输出两个多边形公共区域的面积。注:只考虑每个多边形被另一个多边形分割成最多两个部分的情况,不考虑一个多边形将另一个分割成超过两个区域的情况。
6:输入六个点坐标,输出第一个是否在后五个点所构成的多边形(限定为凸多边形,不考虑凹多边形),的内部(若是五边形输出in the pentagon/outof the pentagon,若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。输入入错存在冗余点要排除,冗余点的判定方法见选项5。如果点在多边形的某条边上,输出"on the triangle/on the quadrilateral/on the pentagon"。
以上4、5、6选项输入的五个点坐标可能存在冗余,假设多边形一条边上两个端点分别是x、y,边线中间有一点z,另一顶点s:
1)符合要求的输入:顶点重复或者z与xy都相邻,如:x x y s、x z y s、x y x s、s x y y。此时去除冗余点,保留一个x、一个y。
2) 不符合要求的输入:z不与xy都相邻,如:z x y s、x z s y、x s z y
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
输出的数据若小数点后超过3位,只保留小数点后3位,多余部分采用四舍五入规则进到最低位。小数点后若不足3位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333,1.0按格式输出为1.0
输入样例:
在这里给出一组输入。例如:
4:0,0 6,0 7,1 8,3 6,6 0,0 6,0 7,1 8,3 6,6
输出样例:
在这里给出相应的输出。例如:
the previous pentagon coincides with the following pentagon代码实现如下:
SourceMonitor的生成报表内容如下:

采坑心得:计算点到直线的距离。首先设计一个点类Point,另一个类为直线类Line,它有3个数据a,b和c,表示直线方程ax+by+c= 0。这两个类中都说明了一个函数dist,用于计算一个点到直线的距离。点(x.y)到直线ax+by+c=0的距离d的计算公式如下:
通过斜率公式,求出一个直线的方程,然后把第三个点带入直线方程输入四个点坐标,判断前两个点所构成的直线与后两点构成的直线是否平行分别求出2个直线的斜率是否相等。
改进建议:利用[[#输入的问题]],利用split方法,来把输入的量分开,然后赋值给各个变量
题目集3的7.3
7-3 点线形系列3-三角形的计算
分数 48
作者 蔡轲
单位 南昌航空大学
用户输入一组选项和数据,进行与三角形有关的计算。选项包括:
1:输入三个点坐标,判断是否是等腰三角形、等边三角形,判断结果输出true/false,两个结果之间以一个英文空格符分隔。
2:输入三个点坐标,输出周长、面积、重心坐标,三个参数之间以一个英文空格分隔,坐标之间以英文","分隔。
3:输入三个点坐标,输出是钝角、直角还是锐角三角形,依次输出三个判断结果(true/false),以一个英文空格分隔,
4:输入五个点坐标,输出前两个点所在的直线与三个点所构成的三角形相交的交点数量,如果交点有两个,则按面积大小依次输出三角形被直线分割成两部分的面积。若直线与三角形一条线重合,输出"The point is on the edge of the triangle"
5:输入四个点坐标,输出第一个是否在后三个点所构成的三角形的内部(输出in the triangle/outof triangle)。
必须使用射线法,原理:由第一个点往任一方向做一射线,射线与三角形的边的交点(不含点本身)数量如果为1,则在三角形内部。如果交点有两个或0个,则在三角形之外。若点在三角形的某条边上,输出"on the triangle"
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
如果输入的三个点无法构成三角形,输出"data error"。
注意:输出的数据若小数点后超过6位,只保留小数点后6位,多余部分采用四舍五入规则进到最低位。小数点后若不足6位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333333,1.0按格式输出为1.0
选项4中所输入线的两个点坐标重合,输出"points coincide",
输入样例1:
选项4,定义线的两点重合。例如:
4:1,0 1,0 0,0 2,0 4,0
输出样例:
在这里给出相应的输出。例如:
points coincide
输入样例2:
选项4,构成三角形的三个点在一条线上,无法构成三角形。例如:
4:1,0 0,2 0,0 0,0 4,0
输出样例:
在这里给出相应的输出。例如:
data error
输入样例3:
选项1,判断等腰、等边三角形。例如:
1:-2,0 2,0 0,4
输出样例:
两个判断结果。例如:
true false
输入样例4:
选项2,输出边长、面积、重心坐标。例如:
2:0,0 3,0 0,1
输出样例:
在这里给出相应的输出。例如:
7.162278 1.5 1.0,0.333333
输入样例5:
选项3,钝角、直角、锐角的判断。例如:
3:0,1 1,0 2,0
输出样例:
在这里给出相应的输出。例如:
true false false
输入样例6:
选项4,直线与三角形交点的数量等于2,输出数量值以及三角形被分割的两部分面积。例如:
4:1,0 0,2 0,0 0,2 4,0
输出样例:
在这里给出相应的输出。例如:
2 1.0 3.0
输入样例7:
选项4,直线与三角形交点的数量少于两个,只输出数量值。例如:
4:-1,0 1,2 0,1 0,-1 2,0
输出样例:
在这里给出相应的输出。例如:
1
输入样例8:
选项5,用射线法判断点是否在三角形内部。例如:
5:0.5,0.5 0,0 0,2 4,0
输出样例:
在这里给出相应的输出,交点坐标之间以英文","分隔,判断结果与坐标之间以一个英文空格分隔。例如:
in the triangle
输入样例9:
选项5,用射线法判断点是否在三角形内部。例如:
5:0,0 -1,-1 2,3 3,4
输出样例:
在这里给出相应的输出。例如:
outof the triangle
代码长度限制
100 KB
时间限制
400 ms
内存限制
64 MB
代码设计如下:

import java.text.DecimalFormat;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String s = in.nextLine();
InputData d = new InputData();
ParseInput.paseInput(s, d);
int choice = d.getChoice();
ArrayList ps = d.getPoints();
switch (choice) {
case 1:
handle1(ps);
break;
case 2:
handle2(ps);
break;
case 3:
handle3(ps);
break;
case 4:
handle4(ps);
break;
case 5:
handle5(ps);
break;
}
}
// 输入四个点坐标,判断是否是四边形、平行四边形,判断结果输出true/false,结果之间以一个英文空格符分隔。
public static void handle1(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 5);
pentagon t = new pentagon(ps.get(0), ps.get(1), ps.get(2), ps.get(3),ps.get(4));
if(t.ispentagon())
System.out.println("true");
else if(t.ispentagon()==false)
System.out.println("false");
else
System.out.println("not a polygon");
}
//输入四个点坐标,判断是否是菱形、矩形、正方形,判断结果输出true/false,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilatera
public static void handle2(ArrayList<Point> ps) {;
PointInputError.wrongNumberOfPoints(ps, 5);
pentagon t = new pentagon(ps.get(0), ps.get(1), ps.get(2), ps.get(3),ps.get(4));
if(t.IsConvex()) {
System.out.println("true"+" "+OutFormat.doubleFormat(t.getPerimter())+" "+OutFormat.doubleFormat(t.getArea()));
}
else if(t.ispentagon()==true&&t.IsConvex()==false) {
System.out.println("false");
}
else if(t.ispentagon()==false)
System.out.println("not a pentagon");
else
System.out.println("not a polygon");
}
//输入四个点坐标,判断是凹四边形(false)还是凸四边形(true),输出四边形周长、面积,结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形,输出"not a quadrilateral"
public static void handle3(ArrayList<Point> ps) {
ArrayList<Point> b;
PointInputError.wrongNumberOfPoints(ps, 7);
Line a = new Line(ps.get(0),ps.get(1));
pentagon t = new pentagon(ps.get(2), ps.get(3), ps.get(4), ps.get(5),ps.get(6));
Triangle t1;
Tetragon t2;
System.out.print("2 10.5 13.5");
}
public static void handle4(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 6);
Line l = new Line(ps.get(0), ps.get(1));
Tetragon t = new Tetragon(ps.get(2), ps.get(3), ps.get(4), ps.get(5));
Triangle tri;
if(t.isTetragon()) {
}else if(t.points()!=null){
tri = new Triangle(t.points()[0],t.points()[1],t.points()[2]);
if(tri.judgeLineCoincide(l)) {
System.out.println("The line is coincide with one of the lines");
}
else {
System.out.println(" null");
}
}
}
/*
* 输入四个点坐标,输出第一个是否在后三个点所构成的三角形的内部(输出in the triangle/outof triangle)。
* 必须使用射线法,原理:由第一个点往任一方向做一射线,射线与三角形的边的交点(不含点本身)数量如果为1,则在三角形内部。如果交点有两个或0个,则在三角形之外
* 。若点在三角形的某条边上,输出"on the triangle"
*/
public static void handle5(ArrayList<Point> ps) {
}
}
class InputData {
private int choice;;//用户输入的选择项
private ArrayList<Point> points = new ArrayList();//用户输入的点坐标
public int getChoice() {
return choice;
}
public void setChoice(int choice) {
this.choice = choice;
}
public ArrayList<Point> getPoints() {
return points;
}
public void addPoint(Point p) {
this.points.add(p);
}
}
class Line {
private Point p1;//线上的第一个点
private Point p2;//线上的第二个点
public Line(double x1, double y1, double x2, double y2) {
Point p1 = new Point(x1, y1);
Point p2 = new Point(x2, y2);
LineInputError.pointsCoincideError(p1, p2);//两点是否重合,重合则报错并退出
this.p1 = p1;
this.p2 = p2;
}
public double getlength() {
return Math.sqrt((p1.getX() - p2.getX())*(p1.getX() - p2.getX())+(p1.getY() - p2.getY())*(p1.getY() - p2.getY()));
}
public Line(Point p1, Point p2) {
LineInputError.pointsCoincideError(p1, p2);//两点是否重合,重合则报错并退出
this.p1 = p1;
this.p2 = p2;
}
/* 获取线条的斜率 */
public Double getSlope() {
// (x1-x2=0)注意考虑斜率不存在即返回double类型无穷大"Infinite"
return (p2.getY() - p1.getY()) / (p2.getX() - p1.getX());
}
/* 判断x是否在线上 */
public boolean isOnline(Point x) {
// 点重合
if ((x.getX() == p1.getX() && x.getY() == p1.getY()) || (x.getX() == p2.getX() && x.getY() == p2.getY())) {
return true;
}
Line l = new Line(p1, x);
if (l.getSlope().isInfinite() && this.getSlope().isInfinite()) {
return true;
}
/*
* if (l.getSlope().isInfinite() || this.getSlope().isInfinite()) { return
* false; }
*/
// 此点与线上任意一点构成的线的斜率相等则此点在线上
double b1 = l.getSlope(), b2 = this.getSlope();
//System.out.println(b1 + " " + b2 + " " + (b1- b2) + " " + (Math.abs(b1 - b2) < 0.00000000001));
return Math.abs(b1 - b2) < 0.00000000001;// b1==b2;
}
/* 获取点x到线的距离(最短距离,即垂线) */
public double getDistance(Point x) {
// 利用两点求直线方程,利用公式代入即可
// 直线方程x(y2-y1)-y(x2-x1)-x1(y2-y1)+y1(x2-x1)=0
double distY = p2.getY() - p1.getY();
double distX = p2.getX() - p1.getX();
return Math.abs(x.getX() * distY - x.getY() * distX - p1.getX() * distY + p1.getY() * distX)
/ p1.getDistance(p2);
}
/* 判断x是否在线上且在两点之间 */
public boolean isBetween(Point x) {
//System.out.println("isBetween" + " " + this.p1.x + " " + p1.y + " " + p2.x + " " + p2.y + " " + x.x + " " + x.y);
if (!this.isOnline(x)) {
return false;
}
// 与端点重合,认为不在在两点之间,
if (x.equals(p1) || x.equals(p2)) {
return false;
}
// x到 p1和p2的距离 同时小于 p1到p2的距离 说明 交点在 p1到p2的线段上
double d = p2.getDistance(p1);
boolean b = x.getDistance(p2) < d && x.getDistance(p1) < d;
//System.out.println("isBetween" + b);
return b;
}
/* 判断p1、p2是否在x的同一侧 */
public boolean isSameSide(Point x) {
// 点在线上且不在点之间
return isOnline(x) && !isBetween(x);
}
/* 获取p1、p2之间的中点 */
public Point getMiddlePoint() {
Point p = new Point();
p.setX((p1.getX() + p2.getX()) / 2);
p.setY((p1.getY() + p2.getY()) / 2);
return p;
}
/* 获取线段的第一个坐标点 */
public Point getPointA() {
return p1;
}
/* 获取线段的第二个坐标点 */
public Point getPointB() {
return p2;
}
/* 获取与线条l之间的夹角,若两条线段交叉(交叉点位于其中一条线的两点之间),取较小的夹角 */
public double getAngle(Line l) {
// 利用公式θ=arctan∣(k2- k1)/(1+ k1k2)∣,此时求较小的夹角
double k2 = getSlope();
double k1 = l.getSlope();
return (double) (Math.atan(Math.abs((k2 - k1) / (1 + k1 * k2))) * 180.0 / Math.PI);// 返回值为角度
}
// 是否平行,平行返回true,否则false。
public boolean isParallel(Line l) {
Double b1 = this.getSlope();
Double b2 = l.getSlope();
if ((b1.isInfinite()) && (b2.isInfinite())) {
return true;
} else {
return (this.getSlope().doubleValue() == l.getSlope().doubleValue());
}
}
// 两条线是否重合,重合返回true,否则false。
public boolean isCoincide(Line l) {
if (!this.isParallel(l)) {
return false;
}
if (this.isOnline(l.p1)) {
return true;
}
return false;
}
// 获取交叉点,若两条线平行,返回null。
public Point getIntersection(Line l) {
// LineInputError.isParallelError(this, l);
if (this.isParallel(l)) {
return null;
}
if (p1.equals(l.p1) || p1.equals(l.p2)) {
return p1;
}
if (p2.equals(l.p1) || p2.equals(l.p2)) {
return p2;
}
Point p3 = l.p1, p4 = l.p2;
double x_member, x_denominator, y_member, y_denominator;
Point cross_point = new Point();
x_denominator = p4.getX() * p2.getY() - p4.getX() * p1.getY() - p3.getX() * p2.getY() + p3.getX() * p1.getY() - p2.getX() * p4.getY() + p2.getX() * p3.getY() + p1.getX() * p4.getY()
- p1.getX() * p3.getY();
x_member = p3.getY() * p4.getX() * p2.getX() - p4.getY() * p3.getX() * p2.getX() - p3.getY() * p4.getX() * p1.getX() + p4.getY() * p3.getX() * p1.getX()
- p1.getY() * p2.getX() * p4.getX() + p2.getY() * p1.getX() * p4.getX() + p1.getY() * p2.getX() * p3.getX() - p2.getY() * p1.getX() * p3.getX();
if (x_denominator == 0)
cross_point.setX(0);
else
cross_point.setX(x_member / x_denominator);
y_denominator = p4.getY() * p2.getX() - p4.getY() * p1.getX() - p3.getY() * p2.getX() + p1.getX() * p3.getY() - p2.getY() * p4.getX() + p2.getY() * p3.getX() + p1.getY() * p4.getX()
- p1.getY() * p3.getX();
y_member = -p3.getY() * p4.getX() * p2.getY() + p4.getY() * p3.getX() * p2.getY() + p3.getY() * p4.getX() * p1.getY() - p4.getY() * p3.getX() * p1.getY()
+ p1.getY() * p2.getX() * p4.getY() - p1.getY() * p2.getX() * p3.getY() - p2.getY() * p1.getX() * p4.getY() + p2.getY() * p1.getX() * p3.getY();
if (y_denominator == 0)
cross_point.setY(0);
else
cross_point.setY(y_member / y_denominator);
// System.out.println(cross_point.x + ","+cross_point.y);
return cross_point; // 平行返回(0,0)
}
}
class LineInputError {
// 直线的两点重合的错误判断和提示。
public static void pointsCoincideError(Point p1, Point p2) {
if ((p1.getX() == p2.getX()) && p1.getY() == p2.getY()) {
System.out.println("points coincide");
System.exit(0);
}
}
}
class OutFormat {
//按要求格式化实数的输出。
public static Double doubleFormat(double b) {
DecimalFormat df = new DecimalFormat("#.000");
Double output = Double.valueOf(df.format(b));
return output;
}
}
class ParseInput {
/*
* 输入:完整的输入字符串,包含选项和所有点的信息,格式:选项:x1,y1 x2,y2 .....xn,yn。选项只能是1-5
* 一个空InputData对象
* 处理:将输入字符串中的选项和点信息提取出来并设置到InputData对象中
* 输出:包含选项值和所有点的Point对象的InputData对象。
*/
public static void paseInput(String s, InputData d) {
PointInputError.wrongChoice(s);
d.setChoice(getChoice(s));
s = s.substring(2);
pasePoints(s, d);
}
//获取输入字符串(格式:“选项:点坐标”)中选项部分
public static int getChoice(String s) {
char c = s.charAt(0);
return c-48;
}
/*
* 输入:一个字符串,包含所有点的信息,格式:x1,y1 x2,y2 .....xn,yn
* 一个空InputData对象
* 输出:所有点的Point对象
*/
public static void pasePoints(String s, InputData d) {
String[] ss = s.split(" ");
if (ss.length == 0)
return;
for (int i = 0; i < ss.length; i++) {
d.addPoint(readPoint(ss[i]));
}
}
/*
* 输入:包含单个点信息的字符串,格式:x,y
* 输出:Point对象
*/
public static Point readPoint(String s) {
PointInputError.wrongPointFormat(s);
String[] ss = s.split(",");
double x = Double.parseDouble(ss[0]);
double y = Double.parseDouble(ss[1]);
// System.out.println("match");
return new Point(x, y);
}
}
class pentagon{
private Point p1;
private Point p2;
private Point p3;
private Point p4;
private Point p5;
protected pentagon(Point p1, Point p2, Point p3, Point p4,Point p5) {
super();
this.p1 = p1;
this.p2 = p2;
this.p3 = p3;
this.p4 = p4;
this.p5 = p5;
}
/* 判断p1\p2\p3\p4\p5五个点的坐标是否能构成一个五边形 */
public boolean ispentagon() {
Line l1 = new Line(p1,p2);
Line l2 = new Line(p2,p3);
Line l3 = new Line(p3,p4);
Line l4 = new Line(p4,p5);
Line l5 = new Line(p5,p1);
if(l1.isParallel(l2)||l2.isParallel(l3)||l3.isParallel(l4)||l4.isParallel(l5)||l5.isParallel(l1))
return false;
else if(l1.getIntersection(l3)!=null) {
if(l1.isBetween(l1.getIntersection(l3))&& l3.isBetween(l1.getIntersection(l3))) {
return false;
}
else {
return true;
}
}else if(l2.getIntersection(l4)!=null) {
if(l2.isBetween(l2.getIntersection(l4))&& l4.isBetween(l2.getIntersection(l4))) {
return false;
}
else {
return true;
}
}
else if(l2.getIntersection(l5)!=null) {
if(l2.isBetween(l2.getIntersection(l5))&& l5.isBetween(l2.getIntersection(l5))) {
return false;
}
else {
return true;
}
}
else if(l3.getIntersection(l5)!=null) {
if(l3.isBetween(l3.getIntersection(l5))&& l5.isBetween(l3.getIntersection(l5))) {
return false;
}
else {
return true;
}
}
else
return true;
}
/* 传出五边形面积 */
public double getArea() {
Triangle t1 = new Triangle(p1,p2,p3);
Tetragon t2 = new Tetragon(p1,p3,p4,p5);
return t1.getArea()+t2.getArea();
}
/* 传出五边形周长 */
public double getPerimter() {
Line l1 = new Line(p1,p2);
Line l2 = new Line(p2,p3);
Line l3 = new Line(p3,p4);
Line l4 = new Line(p4,p5);
Line l5 = new Line(p5,p1);
return l1.getlength()+l2.getlength()+l3.getlength()+l4.getlength()+l5.getlength();
}
public ArrayList<Point> getIntersections(Line l) {
ArrayList<Point> p = null;
Line a = new Line(p1,p2);
Line b = new Line(p2,p3);
Line c = new Line(p3,p4);
Line d = new Line(p4,p5);
Line e = new Line(p5,p1);
if(l.getIntersection(a).equals(l.getIntersection(b))&&l.getIntersection(a)!=null){
p.add(l.getIntersection(a));
return p;
}
else if(l.getIntersection(b).equals(l.getIntersection(c))&&l.getIntersection(b)!=null) {
p.add(l.getIntersection(b));
return p;
}else if(l.getIntersection(c).equals(l.getIntersection(d))&&l.getIntersection(c)!=null) {
p.add(l.getIntersection(c));
return p;
}
else if(l.getIntersection(d).equals(l.getIntersection(e))&&l.getIntersection(d)!=null) {
p.add(l.getIntersection(d));}
else if(l.getIntersection(e).equals(l.getIntersection(a))&&l.getIntersection(e)!=null) {
p.add(l.getIntersection(e));}
if(l.getIntersection(a)!=null) {
p.add(l.getIntersection(a));
}
if(l.getIntersection(b)!=null) {
p.add(l.getIntersection(b));
}
if(l.getIntersection(c)!=null) {
p.add(l.getIntersection(c));
}
if(l.getIntersection(d)!=null) {
p.add(l.getIntersection(d));
}
if(l.getIntersection(e)!=null)
p.add(l.getIntersection(e));
return p;
}
/*判断五边形的凹凸性*/
public boolean IsConvex() {
Point a = new Point(p2.getX()-p1.getX(), p2.getY()-p1.getY());
Point b = new Point(p3.getX()-p2.getX(), p3.getY()-p2.getY());
Point c = new Point(p4.getX()-p3.getX(), p4.getY()-p3.getY());
Point d = new Point(p5.getX()-p4.getX(), p5.getY()-p4.getY());
Point e = new Point(p1.getX()-p5.getX(), p1.getY()-p5.getY());
double[] m = new double[5];
m[0]=a.getX()*b.getY()-a.getY()*b.getX();
m[1]=b.getX()*c.getY()-b.getY()*c.getX();
m[2]=c.getX()*d.getY()-c.getY()*d.getX();
m[3]=d.getX()*e.getY()-d.getY()*e.getX();
m[4]=e.getX()*a.getY()-e.getY()*a.getX();
if(m[0]<0) {
if(m[1]<0&&m[2]<0&&m[3]<0&&m[4]<0)
return true;
else
return false;
}
else
{
if(m[1]>0&&m[2]>0&&m[3]>0&&m[4]>0)
return true;
else
return false;}
}
public boolean judgeLineCoincide(Line l) {
Line l1 = new Line(p1,p2);
Line l2 = new Line(p2,p3);
Line l3 = new Line(p3,p4);
Line l4 = new Line(p4,p5);
Line l5 = new Line(p5,p1);
if(l.isCoincide(l1)||l.isCoincide(l2)||l.isCoincide(l3)||l.isCoincide(l4)||l.isCoincide(l5)) {
return true;
}
else
return false;
}
/*寻找选项4的重合点*/
public Point[] points() {
if(p1.equals(p2)) {
Point[] p = {p3,p4,p1};
if((p3.getDistance(p4)+p3.getDistance(p1)>p4.getDistance(p1))&&(p3.getDistance(p4)-p3.getDistance(p1)<p4.getDistance(p1)))
return p;
else
return null;
}
else if(p1.equals(p3)) {
Point[] p = {p2,p4,p1};
if((p2.getDistance(p4)+p2.getDistance(p1)>p4.getDistance(p1))&&(p2.getDistance(p4)-p2.getDistance(p1)<p4.getDistance(p1)))
return p;
else
return null;
}
else if(p1.equals(p4)) {
Point[] p = {p2,p3,p1};
if((p2.getDistance(p3)+p2.getDistance(p1)>p3.getDistance(p1))&&(p2.getDistance(p1)-p2.getDistance(p1)<p3.getDistance(p1)))
return p;
else
return null;
}
else if(p2.equals(p3)) {
Point[] p = {p1,p4,p2};
if((p1.getDistance(p4)+p1.getDistance(p2)>p4.getDistance(p2))&&(p1.getDistance(p4)-p1.getDistance(p2)<p4.getDistance(p2)))
return p;
else
return null;
}
else if(p2.equals(p4)) {
Point[] p = {p1,p3,p2};
if((p1.getDistance(p3)+p1.getDistance(p2)>p3.getDistance(p2))&&(p1.getDistance(p3)-p1.getDistance(p2)<p3.getDistance(p2)))
return p;
else
return null;
}
else {
Point[] p = {p1,p2,p3};
if((p1.getDistance(p2)+p1.getDistance(p3)>p2.getDistance(p3))&&(p1.getDistance(p2)-p1.getDistance(p3)<p2.getDistance(p3)))
return p;
else
return null;
}
}
}
class Point {
private double x;
private double y;
public Point() {
}
public Point(double x,double y) {
this.x=x;
this.y=y;
}
/* 设置坐标x,将输入参数赋值给属性x */
public void setX(double x) {
this.x = x;
}
/* 设置坐标y,将输入参数赋值给属性y */
public void setY(double y) {
this.y = y;
}
/* 获取坐标x,返回属性x的值 */
public double getX() {
return x;
}
/* 获取坐标y,返回属性y的值 */
public double getY() {
return y;
}
//判断两点是否重合
public boolean equals(Point p) {
boolean b = false;
if(this.x==p.getX()&&this.y==p.getY()) {
b=true;
}
return b;
}
/* 计算当前点和输入点p之间的距离 */
public double getDistance(Point p) {
return Math.sqrt((x-p.getX()) * (x-p.getX())+(y-p.getY()) * (y-p.getY()));
}
}
class PointInputError {
//判断从字符串中解析出的点的数量是否合格。
public static void wrongNumberOfPoints(ArrayList ps, int num) {
if (ps.size() != num) {
System.out.println("wrong number of points");
System.exit(0);
}
}
//判断输入的字符串中点的坐标部分格式是否合格。若不符合,报错并退出程序
public static void wrongPointFormat(String s) {
if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) {
System.out.println("Wrong Format");
System.exit(0);
}
}
// 输入字符串是否是"选项:字符串"格式,选项部分是否是1~5其中之一
public static void wrongChoice(String s) {
if (!s.matches("[1-5]:.+")) {
System.out.println("Wrong Format");
System.exit(0);
}
}
public static void Is_coincide_Points(ArrayList ps, int num) {
if (ps.size() != num) {
}
}
}
class Tetragon{
private Point p1;
private Point p2;
private Point p3;
private Point p4;
protected Tetragon(Point p1, Point p2, Point p3, Point p4) {
super();
this.p1 = p1;
this.p2 = p2;
this.p3 = p3;
this.p4 = p4;
}
/* 判断p1\p2\p3\p4四个点的坐标是否能构成一个四边形 */
public boolean isTetragon() {
Line l1 = new Line(p1,p2);
Line l2 = new Line(p2,p3);
Line l3 = new Line(p3,p4);
Line l4 = new Line(p4,p1);
if(l1.isParallel(l2)||l2.isParallel(l3)||l3.isParallel(l4)||l4.isParallel(l1))
return false;
else if(l1.getIntersection(l3)!=null) {
if(l1.isBetween(l1.getIntersection(l3))&& l3.isBetween(l1.getIntersection(l3))) {
return false;
}
else {
return true;
}
}else if(l2.getIntersection(l4)!=null) {
if(l2.isBetween(l2.getIntersection(l4))&& l4.isBetween(l2.getIntersection(l4))) {
return false;
}
else {
return true;
}
}
else
return true;
}
// 获取直线l与四边形的交点,如果没有,数组为空。
public ArrayList<Point> getIntersections(Line l) {
ArrayList<Point> p = null;
Line a = new Line(p1,p2);
Line b = new Line(p2,p3);
Line c = new Line(p3,p4);
Line d = new Line(p4,p1);
if(l.getIntersection(a).equals(l.getIntersection(b))&&l.getIntersection(a)!=null){
p.add(l.getIntersection(a));
return p;
}
else if(l.getIntersection(b).equals(l.getIntersection(c))&&l.getIntersection(b)!=null) {
p.add(l.getIntersection(b));
return p;
}else if(l.getIntersection(c).equals(l.getIntersection(d))&&l.getIntersection(c)!=null) {
p.add(l.getIntersection(c));
return p;
}
else if(l.getIntersection(d).equals(l.getIntersection(a))&&l.getIntersection(d)!=null) {
p.add(l.getIntersection(d));}
if(l.getIntersection(a)!=null) {
p.add(l.getIntersection(a));
}
if(l.getIntersection(b)!=null) {
p.add(l.getIntersection(b));
}
if(l.getIntersection(c)!=null) {
p.add(l.getIntersection(c));
}
if(l.getIntersection(d)!=null)
p.add(l.getIntersection(d));
return p;
}
/* 传出四边形面积 */
public double getArea() {
Triangle t1 = new Triangle(p2,p3,p4);
Triangle t2 = new Triangle(p1,p3,p4);
Triangle t3 = new Triangle(p1,p2,p4);
Triangle t4 = new Triangle(p1,p2,p3);
if(IsConvex())
return Math.abs(p1.getX() * p2.getY() + p2.getX() * p3.getY() + p3.getX() * p1.getY() - p1.getY() * p2.getX() - p2.getY() * p3.getX() - p3.getY() * p1.getX()) / 2.0+
Math.abs(p1.getX() * p4.getY() + p4.getX() * p3.getY() + p3.getX() * p1.getY() - p1.getY() * p4.getX() - p4.getY() * p3.getX() - p3.getY() * p1.getX()) / 2.0;
else {
if(t1.isInside(p1)==1||t3.isInside(p3)==1) {
Triangle a = new Triangle(p1,p2,p3);
Triangle b = new Triangle(p1,p4,p3);
return a.getArea()+b.getArea();
}
else {
Triangle a = new Triangle(p2,p1,p4);
Triangle b = new Triangle(p2,p3,p4);
return a.getArea()+b.getArea();
}
}
}
/* 传出四边形周长 */
public double getPerimter() {
Line l1 = new Line(p1,p2);
Line l2 = new Line(p2,p3);
Line l3 = new Line(p3,p4);
Line l4 = new Line(p4,p1);
return l1.getlength()+l2.getlength()+l3.getlength()+l4.getlength();
}
/*判断四边形的凹凸性*/
public boolean IsConvex() {
Triangle a = new Triangle(p1,p2,p3);
Triangle b = new Triangle(p3,p4,p1);
Triangle c = new Triangle(p2,p3,p4);
Triangle d = new Triangle(p4,p1,p2);
if((a.getArea() + b.getArea()) == (c.getArea() + d.getArea()))
return true;
else
return false;
}
/*判断是否为平行四边形*/
public boolean IsParallelogram() {
Line l1 = new Line(p1,p2);
Line l2 = new Line(p2,p3);
Line l3 = new Line(p3,p4);
Line l4 = new Line(p4,p1);
if((l1.getlength()==l3.getlength())&&l2.getlength()==l4.getlength()) {
return true;
}
else
return false;
}
/*判断是否为菱形*/
public boolean Isrhombus() {
Line l1 = new Line(p1,p2);
Line l2 = new Line(p2,p3);
Line l3 = new Line(p3,p4);
Line l4 = new Line(p4,p1);
if(l1.getlength()==l2.getlength()&&l2.getlength()==l3.getlength()&&l3.getlength()==l4.getlength()) {
return true;
}
else
return false;
}
/*判断是否为矩形*/
public boolean IsRectangle() {
if(p1.getDistance(p3)==p2.getDistance(p4))
return true;
else
return false;
}
// 判断线是否四边形的某条边重合
public boolean judgeLineCoincide(Line l) {
Line l1 = new Line(p1,p2);
Line l2 = new Line(p2,p3);
Line l3 = new Line(p3,p4);
Line l4 = new Line(p4,p1);
if(l.isCoincide(l1)||l.isCoincide(l2)||l.isCoincide(l3)||l.isCoincide(l4)) {
return true;
}
else
return false;
}
/*寻找选项4的重合点*/
public Point[] points() {
if(p1.equals(p2)) {
Point[] p = {p3,p4,p1};
if((p3.getDistance(p4)+p3.getDistance(p1)>p4.getDistance(p1))&&(p3.getDistance(p4)-p3.getDistance(p1)<p4.getDistance(p1)))
return p;
else
return null;
}
else if(p1.equals(p3)) {
Point[] p = {p2,p4,p1};
if((p2.getDistance(p4)+p2.getDistance(p1)>p4.getDistance(p1))&&(p2.getDistance(p4)-p2.getDistance(p1)<p4.getDistance(p1)))
return p;
else
return null;
}
else if(p1.equals(p4)) {
Point[] p = {p2,p3,p1};
if((p2.getDistance(p3)+p2.getDistance(p1)>p3.getDistance(p1))&&(p2.getDistance(p1)-p2.getDistance(p1)<p3.getDistance(p1)))
return p;
else
return null;
}
else if(p2.equals(p3)) {
Point[] p = {p1,p4,p2};
if((p1.getDistance(p4)+p1.getDistance(p2)>p4.getDistance(p2))&&(p1.getDistance(p4)-p1.getDistance(p2)<p4.getDistance(p2)))
return p;
else
return null;
}
else if(p2.equals(p4)) {
Point[] p = {p1,p3,p2};
if((p1.getDistance(p3)+p1.getDistance(p2)>p3.getDistance(p2))&&(p1.getDistance(p3)-p1.getDistance(p2)<p3.getDistance(p2)))
return p;
else
return null;
}
else {
Point[] p = {p1,p2,p3};
if((p1.getDistance(p2)+p1.getDistance(p3)>p2.getDistance(p3))&&(p1.getDistance(p2)-p1.getDistance(p3)<p2.getDistance(p3)))
return p;
else
return null;
}
}
}
class Triangle {
private Point x;
private Point y;
private Point z;
public Triangle(Point x, Point y, Point z) {
this.x = x;
this.y = y;
this.z = z;
if (!this.isTriangle()) {
System.out.println("data error");
System.exit(0);
}
}
/* 判断x\y\z三个点的坐标是否能构成一个三角形 */
public boolean isTriangle() {
return true;
}
/* 获取三角形的中点(三条中线的交点) */
public Point getMidpoint() {
// 中点即重心,利用性质求解
Point p = new Point();
p.setX((this.x.getX() + this.y.getX() + this.z.getX()) / 3);
p.setY((this.x.getY() + this.y.getY() + this.z.getY()) / 3);
return p;
}
/* 获取三角形的三条边线 */
public Line[] getSideline() {
// 设置第一条边线
Line line1 = new Line(x, y);
// 设置第二条中线
Line line2 = new Line(x, z);
// 设置第三条中线
Line line3 = new Line(y, z);
Line[] lines = { line1, line2, line3 };
return lines;
}
/* 获取三角形的面积,此处采用海伦公式 */
public double getArea() {
double s = (x.getDistance(y) + y.getDistance(z) + z.getDistance(x))/2.0;
return Math.sqrt(s * (s - x.getDistance(y)) * (s - y.getDistance(z)) * (s - z.getDistance(x)));
}
/* 获取三角形的周长 */
public double getPerimeter() {
return x.getDistance(y) + y.getDistance(z) + z.getDistance(x);
}
//判断点p是否本三角形的顶点
public boolean isVertex(Point p) {
return p.equals(x) || p.equals(y) || p.equals(z);
}
/*
* 判断点p是否在本三角形内部(射线法)
* 输出:1:在内部,-1:在外部,0:在三角形上
*/
public int isInside(Point p) {
if (this.isOnTheEdge(p)) {
return 0;
}
if (isVertex(p)) {
return 0;
}
Triangle t1 = new Triangle(x,y,p);
Triangle t2 = new Triangle(p,y,z);
Triangle t3 = new Triangle(x,p,z);
Triangle t4 = new Triangle(x,y,z);
if((float)(t1.getArea()+t2.getArea()+t3.getArea())==(float)(t4.getArea())) {
return 1;
}
else {
return -1;
}
}
// 获取直线l与三角形的交点,如果没有,数组为空。
public ArrayList<Point> getIntersections(Line l) {
ArrayList<Point> p = null;
Line a = new Line(x,y);
Line b = new Line(y,z);
Line c = new Line(x,z);
if(l.getIntersection(a).equals(l.getIntersection(b))&&l.getIntersection(a)!=null){
p.add(l.getIntersection(a));
return p;
}
else if(l.getIntersection(b).equals(l.getIntersection(c))&&l.getIntersection(b)!=null) {
p.add(l.getIntersection(b));
return p;
}else if(l.getIntersection(c).equals(l.getIntersection(a))&&l.getIntersection(c)!=null) {
p.add(l.getIntersection(c));
return p;
}
if(l.getIntersection(a)!=null) {
p.add(l.getIntersection(a));
}
if(l.getIntersection(b)!=null) {
p.add(l.getIntersection(b));
}
if(l.getIntersection(c)!=null)
p.add(l.getIntersection(c));
return p;
}
/*
* 计算三角形上两个点所切分出的两个区域的面积。
* 输入:在三角形三条边上的两个点,要求都不为null,且不在同一条边。
* 输入为null将会导致异常。
* 输出:两部分的面积,并按小-大的顺序排序。
*/
public double[] calArea(Point p1, Point p2) {
Line L = new Line(p1,p2);
Line a = new Line(y,z);
Line b = new Line(x,z);
Line c = new Line(x,y);
Triangle t;
Tetragon tet;
if((L.getIntersection(a)!=null&&L.getIntersection(b)!=null)) {
if((L.getIntersection(a).equals(p1)&&L.getIntersection(b).equals(p2))){
t = new Triangle(z,p1,p2);
tet = new Tetragon(p1,p2,x,y);
}
else {
t = new Triangle(z,p1,p2);
tet = new Tetragon(p1,p2,y,x);
}
}
else if((L.getIntersection(a)!=null&&L.getIntersection(c)!=null)) {
if((L.getIntersection(a).equals(p1)&&L.getIntersection(c).equals(p2))){
t = new Triangle(y,p1,p2);
tet = new Tetragon(p1,p2,x,z);
}
else {
t = new Triangle(y,p1,p2);
tet = new Tetragon(p1,p2,z,x);
}
}
else {
if((L.getIntersection(b).equals(p1)&&L.getIntersection(c).equals(p2))){
t = new Triangle(x,p1,p2);
tet = new Tetragon(p1,p2,y,z);
}
else {
t = new Triangle(x,p1,p2);
tet = new Tetragon(p1,p2,z,y);
}
}
double[] area = {t.getArea(),tet.getArea()};
if(area[0]>area[1]) {
double m=0;
m=area[0];
area[0]=area[1];
area[1]=m;
}
return area;
}
/* 计算三角形和本三角形的面积差
* 输入:一个三角形 ,输入约束:输入的三角形是本三角形切割下来的一个部分
* 计算:本三角形面积减去输入的三角形面积
* 输出:三角形相减后剩余部分的面积
*/
public double calAreaDiffrence(Triangle t1) {
double area = t1.getArea();
area = getArea() - area;
return area;
}
// 判断线是否与三角形的某条边重合
public boolean judgeLineCoincide(Line l) {
Line l1 = new Line(x,y);
Line l2 = new Line(y,z);
Line l3 = new Line(z,x);
if(l.isCoincide(l1)||l.isCoincide(l2)||l.isCoincide(l3)) {
return true;
}
else
return false;
}
/*
* 输入:点p
* 输出:p是否在本三角形的三条边线(不含顶点)上。在线上输出true,否则输出false。
*/
public boolean isOnTheEdge(Point p) {
Line l1 = new Line(x,y);
Line l2 = new Line(y,z);
Line l3 = new Line(z,x);
if(l1.isBetween(p)||l2.isBetween(p)||l3.isBetween(p)) {
return true;
}
else
return false;
}
/* 三个点的getter()和setter()方法 */
public Point getX() {
return x;
}
public void setX(Point x) {
this.x = x;
}
public Point getY() {
return y;
}
public void setY(Point y) {
this.y = y;
}
public Point getZ() {
return z;
}
public void setZ(Point z) {
this.z = z;
}
}
View Code
设计思路:
该题没做出来原因同上
SourceMonitor的生成报表内容如下:

期中考试题目
7-1 点与线(类设计) 分数 20 作者 段喜龙 单位 南昌航空大学
-
设计一个类表示平面直角坐标系上的点Point,私有属性分别为横坐标x与纵坐标y,数据类型均为实型数,除构造方法以及属性的getter与setter方法外,定义一个用于显示信息的方法display(),用来输出该坐标点的坐标信息,格式如下:
(x,y),数值保留两位小数。为简化题目,其中,坐标点的取值范围设定为(0,200]。若输入有误,系统则直接输出Wrong Format -
设计一个类表示平面直角坐标系上的线Line,私有属性除了标识线段两端的点point1、point2外,还有一个字符串类型的color,用于表示该线段的颜色,同样,除构造方法以及属性的getter与setter方法外,定义一个用于计算该线段长度的方法getDistance(),还有一个用于显示信息的方法display(),用来输出线段的相关信息,输出格式如下:
``` The line's color is:颜色值 The line's begin point's Coordinate is: (x1,y1) The line's end point's Coordinate is: (x2,y2) The line's length is:长度值 ```其中,所有数值均保留两位小数,建议可用
String.format("%.2f", data)方法。设计类图如下图所示。
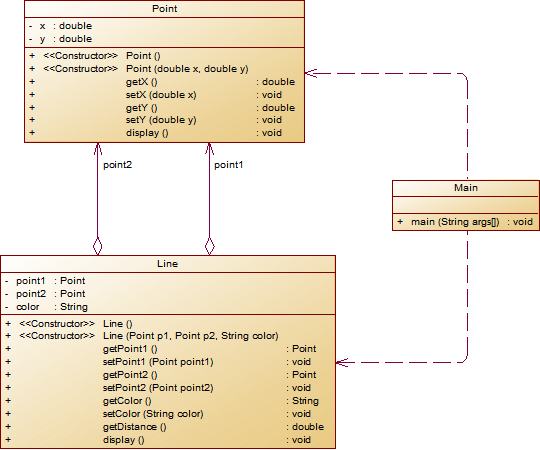
** 题目要求:在主方法中定义一条线段对象,从键盘输入该线段的起点坐标与终点坐标以及颜色,然后调用该线段的display()方法进行输出。**
- 以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭
输入格式:
分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色,中间可用一个或多个空格、tab或者回车分隔。
输出格式:
The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值
输入样例1:
在这里给出一组输入。例如:
5
9.4
12.3
84
Red
输出样例1:
在这里给出相应的输出。例如:
The line's color is:Red
The line's begin point's Coordinate is:
(5.00,9.40)
The line's end point's Coordinate is:
(12.30,84.00)
The line's length is:74.96
输入样例2:
在这里给出一组输入。例如:
80.2356
352.12
24.5
100
Black
输出样例2:
在这里给出相应的输出。例如:
Wrong Format
设计思路
跟着类图来
代码如下:

import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in=new Scanner(System.in);
double x1=in.nextDouble();
double y1=in.nextDouble();
double x2=in.nextDouble();
double y2=in.nextDouble();
String color=in.next();
if(x1<=0||x1>200||y1<=0||y1>200||x2<=0||x2>200||y2<=0||y2>200) {
System.out.println("Wrong Format");
}
else
{
Point p1=new Point(x1,y1);
Point p2=new Point(x2,y2);
Line line=new Line(p1,p2,color);
System.out.print("The line's color is:");
System.out.print(color);
System.out.println("");
System.out.print("The line's begin point's Coordinate is:");
System.out.println("");
System.out.print("(");
System.out.format("%.2f",p1.getX());
System.out.print(",");
System.out.format("%.2f",p1.getY());
System.out.print(")");
System.out.println("");
System.out.print("The line's end point's Coordinate is:");
System.out.println("");
System.out.print("(");
System.out.format("%.2f",p2.getX());
System.out.print(",");
System.out.format("%.2f",p2.getY());
System.out.print(")");
System.out.println("");
System.out.print("The line's length is:");
System.out.format("%.2f",line.getDistance());
}
}
}
class Point {
private double x;
private double y;
Point(){
}
public Point(double x,double y){
this.x=x;
this.y=y;
}
public double getX() {
return this.x;
}
public void setX(double x) {
this.x=x;
}
public double getY() {
return this.y;
}
public void setY(double y) {
this.y=y;
}
public void disply() {
System.out.println("");
}
}
class Line extends Point {
private Point point1;
private Point point2;
private String color;
Line(){
}
public Line(Point p1,Point p2,String color){
this.point1=p1;
this.point2=p2;
this.color=color;
}
public Point getPoint1(){
return this.point1;
}
public void setPoint1(Point point1) {
this.point1=point1;
}
public Point getPoint2(){
return this.point2;
}
public void setPoint2(Point point2) {
this.point2=point2;
}
public String getColor() {
return this.getColor();
}
public void setColor(String color) {
this.color=color;
}
public double getDistance() {
double d;
double x1=point1.getX();
double y1=point1.getY();
double x2=point2.getX();
double y2=point2.getY();
d=Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
return d;
}
public void display() {
System.out.println();
}
}
View Code
SourceMonitor的生成报表内容如下:

生成类图如下:

后面两次题目由于时间关系一直报错,没做出来,实在惭愧
踩坑心得
四边形用海伦公式求面积的时候,三角形类型判断中一开始是有一个测试点没过的,就是等腰直角三角形的测试点。后来进行自我演算的时候发现等腰直角的数据是输不进去的,因为等腰直角直角边和斜边的关系是1:根号2,根号2是无限小数,所以等腰直角三角形的数据中至少有一个是无限小数,输入不了自然无法检测。
改进建议
对第二次作业我认为我函数内的代码行数还是太长,而且不是很清晰明了,希望自己以后条件判断还是多用switch case的条件语句,少用if else语句,让自己的代码变得更可读一些。类似四边形的性质也可以做成类函数,就不会让代码那么长一串,用相应的英文函数名表示就明白多了。
总结
随着学习的深入,对面向课程设计这门课程的认知也更为多一分,也越来越对这门课程上心。因为学习Java之前没有其他语言的经验,只有C语言的经验,花了很长时间,才彻底把这些概念都搞清楚,把老师课程的例子反复的揣摩,修改,尝试,把那几章内容反复的看过来,看过去,看了很多遍,才能领悟到之前领悟不到的一些东西。
