「Luogu P2501」[HAOI2006] 数字序列

题目

现在我们有一个长度为 \(n\) 的整数序列 \(a\)。但是它太不好看了，于是我们希望把它变成一个单调严格上升的序列。但是不希望改变过多的数，也不希望改变的幅度太大。

Luogu

分析

首先考虑 subtask 1: 最小化要修改的数。

如果正面思考一个数修改或不修改的答案，会发现答案的更新依赖于前一个数具体的修改方案，问题就变得非常棘手。这时不妨反过来考虑，什么样的数可以不修改？假设我们保留 \(a_{i}\) 和 \(a_{j}\) 不变，其中 \(i<j\)，根据条件必然有 \(a_{j} - a_{i} \geq j - i\), 移项之后可以得到 \(a_{j}-j\geq a_{i}-i\), 在 \(a\) 数组中所有邻项分别满足这个不等式子序列就是可以不修改的子序列，令 \(b_{i}=a_{i}-i\)，于是问题转化为了求 \(b\) 数组的最长不下降子序列，这个直接套公式就可以了。

然后考虑 subtask 2: 最小化改变量的绝对值。

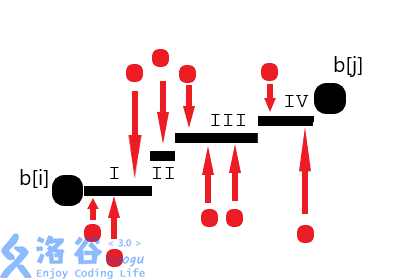
修改 \(a\) 为严格上升序列相当于修改 \(b\) 为不下降序列，不妨直接在 \(b\) 上修改。设 \(b_{l}\) 与 \(b_{r}\) 是求出的最长不下降子序列中相邻的两个数，我们的任务是修改 \(l+1 \sim r-1\) 这部分的数。直接 DP 枚举可能的取值仍然依赖于前一个数的具体值，非常麻烦，不妨先随便选一个合法的方案然后试着对它做修改来尽可能减小修改量。对于这种序列大小相关的题，常将其看作为柱状图、折线图等来视觉化方便进一步思考，这里邻项可以相等的情况不妨考虑下列阶梯图的形式：

^[1]

从图中很容易看出，如果一个阶梯上的点，位于其上方的点和下方的点数目一致的话（方便起见，记这个条件为 \(A\)），那么这个阶梯上下移动的过程中这些点修改量之和都不会变化，而阶梯的高度必然是递增的，此时我们可以想一个极端情况：将 \(l+1 \sim r-1\) 所有数都修改为 \(b_{l}\), 然后依次考虑拔高 \(i \sim r-1\) 表示的阶梯。显然一开始的点若小于等于 \(b_{l}\) 的话肯定不会拔高这个阶梯，若 \(b_{i} > b_{l}\)，我们考虑拔高 \(i \sim r-1\), 显然只有拔高到能使这个阶梯满足 \(A\) 时才是最优，如果不管怎么拔高都无法满足 \(A\) 的话说明一开始就低于阶梯的点要多于高于阶梯的点，拔高只会使答案更大，因此此时就保持不变继续考虑下一个点直到能满足 \(A\). 假设在点 \(m\) 处成功通过拔高 \(m \sim r-1\) 的阶梯满足了 \(A\), 就会发现此时已经是最优解了：将上图旋转 90° 看，\(m \sim r - 1\) 这一段的答案就是将阶梯左边的点与右边的点任意两两配对得到的线段长度之和，显然这些点的答案之和不可能小于这个值，因此我们只要找到第一个能满足 \(A\) 的点即可得到答案，恰好是左右两段阶梯（不包括 \(b_{r}\) 的话）。

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

int gi() { // 还在用 gi() 是因为这是 23 年的代码（
    int x = 0, f = 1; char c = getchar();
    for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
    for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
    return x * f;
}

const int N = 35005;
const int INF = 1e9;

int n;
ll f[N], pre[N], suf[N];
int a[N], b[N], len[N], dp[N];

vector <int> vec[N];

int main() {
    n = gi();
    for (int i = 1; i <= n; ++i) a[i] = gi(), b[i] = a[i] - i;
    b[0] = -INF, b[n + 1] = INF;
    int mx = 0;
    for (int i = 1; i <= n + 1; ++i) {
        int l = 1, r = mx;
        while (l <= r) {
            int mid = l + r >> 1;
            if (len[mid] <= b[i]) l = mid + 1;
            else r = mid - 1;
        }
        dp[i] = l, len[l] = b[i];
        vec[l].push_back(i);
        mx = max(mx, l);
    }
    mx--;
    vec[0].push_back(0);
    memset(f, 0x3f3f3f3f, sizeof f);
    f[0] = 0;
    for (int i = 1; i <= n + 1; ++i) {
        for (int j = 0; j < vec[dp[i] - 1].size(); ++j) {
            int from = vec[dp[i] - 1][j];
            if (b[from] > b[i] || from > i) continue;
            pre[from] = 0, suf[i] = 0;
            for (int k = from + 1; k < i; ++k) pre[k] = pre[k - 1] + abs(b[k] - b[from]);
            for (int k = i - 1; k > from; --k) suf[k] = suf[k + 1] + abs(b[k] - b[i]);
            for (int k = from; k < i; ++k) f[i] = min(f[i], f[from] + pre[k] + suf[k + 1]);
        }
    }
    printf("%d\n%lld\n", n - mx, f[n + 1]);
    return 0;
}