前言

J 组本来可以 AK 的，但是对于 DP 的敏感度太低了，导致 T4 赛时没有往 DP 上面想。

正片

T1：扑克牌

题目描述

小 P 从同学小 Q 那儿借来一副 \(n\) 张牌的扑克牌。
本题中我们不考虑大小王，此时每张牌具有两个属性：花色和点数。花色共有 \(4\) 种：方片、草花、红桃和黑桃。点数共有 \(13\) 种，从小到大分别为 \(\tt{A 2 3 4 5 6 7 8 9 T J Q K}\)。注意：点数 \(10\) 在本题中记为 \(\tt T\)。
我们称一副扑克牌是完整的，当且仅当对于每一种花色和每一种点数，都恰好有一张牌具有对应的花色和点数。由此，一副完整的扑克牌恰好有 \(4 \times 13 = 52\) 张牌。以下图片展示了一副完整的扑克牌里所有的 52 张牌。

小 P 借来的牌可能不是完整的，为此小 P 准备再向同学小 S 借若干张牌。可以认为小 S 每种牌都有无限张，因此小 P 可以任意选择借来的牌。小 P 想知道他至少得向小 S 借多少张牌，才能让从小 S 和小 Q 借来的牌中，可以选出 \(52\) 张牌构成一副完整的扑克牌。
为了方便你的输入，我们使用字符 \(\tt D\) 代表方片，字符 \(\tt C\) 代表草花，字符 \(\tt H\) 代表红桃，字符 \(\tt S\) 代表黑桃，这样每张牌可以通过一个长度为 \(2\) 的字符串表示，其中第一个字符表示这张牌的花色，第二个字符表示这张牌的点数，例如 \(\tt{CA}\) 表示草花 \(\tt A\)，\(\tt{ST}\) 表示黑桃 \(\tt T\)（黑桃 10）。

思路

STL 的板子题，把输入当作一个字符串就可以了，用 map 或者 set 都可以过。

代码就不放了。

T2：地图探险

题目描述

小 A 打算前往一片丛林去探险。丛林的地理环境十分复杂，为了防止迷路，他先派遣了一个机器人前去探路。
丛林的地图可以用一个 \(n\) 行 \(m\) 列的字符表来表示。我们将第 \(i\) 行第 \(j\) 列的位置的坐标记作 \((i, j)(1 \leq i \leq n, 1 \leq j \leq m)\)。如果这个位置的字符为 \(\tt x\)，即代表这个位置上有障碍，不可通过。反之，若这个位置的字符为 \(\tt.\)，即代表这个位置是一片空地，可以通过。
这个机器人的状态由位置和朝向两部分组成。其中位置由坐标 \((x, y)(1 \leq x \leq n, 1 \leq y \leq m)\) 刻画，它表示机器人处在地图上第 \(x\) 行第 \(y\) 列的位置。而朝向用一个 \(0 \sim 3\) 的 整数 \(d\) 表示，其中 \(d = 0\) 代表向东，\(d = 1\) 代表向南，\(d = 2\) 代表向西，\(d = 3\) 代表向北。
初始时，机器人的位置为 \((x_0, y_0)\)，朝向为 \(d_0\)。保证初始时机器人所在的位置为空地。接下来机器人将要进行 \(k\) 次操作。每一步，机器人将按照如下的模式操作：

1. 假设机器人当前处在的位置为 \((x, y)\)，朝向为 \(d\)。则它的方向上的下一步的位置 \((x^′, y^′)\) 定义如下：若 \(d = 0\)，则令 \((x^′, y^′) = (x, y + 1)\)，若 \(d = 1\)，则令 \((x^′, y^′) = (x + 1, y)\)，若 \(d = 2\)，则令 \((x^′, y^′) = (x, y - 1)\)，若 \(d = 3\)，则令 \((x^′, y^′) = (x - 1, y)\)。
2. 接下来，机器人判断它下一步的位置是否在地图内，且是否为空地。具体地说，它判断 \((x^′, y^′)\) 是否满足 \(1 \leq x^′ \leq n, 1 \leq y^′ \leq m\)，且 \((x^′, y^′)\) 位置上是空地。如果条件成立，则机器人会向前走一步。它新的位置变为 \((x^′, y^′)\)，且朝向不变。如果条件不成立，则它会执行“向右转”操作。也就是说，令 \(d^′ = (d + 1) \bmod 4\)（即 \(d + 1\) 除以 \(4\) 的余数），且它所处的位置保持不变，但朝向由 \(d\) 变为 \(d^′\)。
   小 A 想要知道，在机器人执行完 \(k\) 步操作之后，地图上所有被机器人经过的位置（包括起始位置）有几个。

思路

直接模拟即可，注意变量名的取名，不然可能就会编译出错。

T3：小木棍

题目描述

小 S 喜欢收集小木棍。在收集了 \(n\) 根长度相等的小木棍之后，他闲来无事，便用它们拼起了数字。用小木棍拼每种数字的方法如下图所示。

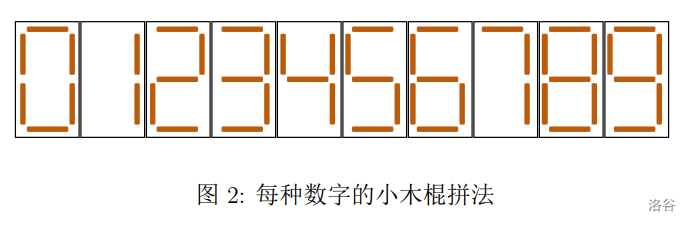
现在小 S 希望拼出一个正整数，满足如下条件：

• 拼出这个数恰好使用 \(n\) 根小木棍；
• 拼出的数没有前导 \(0\)；
• 在满足以上两个条件的前提下，这个数尽可能小。
  小 S 想知道这个数是多少，可 \(n\) 很大，把木棍整理清楚就把小 S 折腾坏了，所以你需要帮他解决这个问题。如果不存在正整数满足以上条件，你需要输出 \(-1\) 进行报告。

思路

根据特殊性质 A 和 B，可以发现这道题目要求数最小的前提条件下就是数的位数首先要最小，并且在 \(0,1,2,3,4,5,6,7,8,9\) 中 \(8\) 占用的木棍条数是最多的。那么优先考虑一直放 \(8\)，我们就按照 \(n\) 对于 \(7\) 的模数进行分类讨论：

以下的除法都默认为向下取证。

\(n\equiv 0\) \(mod\) \(7\)，输出 \(\frac{n}{7}\) 个 \(8\)。

\(n\equiv 1\) \(mod\) \(7\)，输出 \(\frac{n-7}{7}\) 个 \(8\) 然后拼凑出 \(8\) 个木棍即可。

以此类推。

T4：接龙

题目描述

在玩惯了成语接龙之后，小 J 和他的朋友们发明了一个新的接龙规则。
总共有 \(n\) 个人参与这个接龙游戏，第 \(i\) 个人会获得一个整数序列 \(S_i\) 作为他的词库。
一次游戏分为若干轮，每一轮规则如下：

• \(n\) 个人中的某个人 \(p\) 带着他的词库 \(S_p\) 进行接龙。若这不是游戏的第一轮，那么这一轮进行接龙的人不能与上一轮相同，但可以与上上轮或更往前的轮相同。
• 接龙的人选择一个长度在 \([2, k]\) 的 \(S_p\) 的连续子序列 \(A\) 作为这一轮的接龙序列，其中 \(k\) 是给定的常数。若这是游戏的第一轮，那么 \(A\) 需要以元素 \(1\) 开头，否则 \(A\) 需要以上一轮的接龙序列的最后一个元素开头。
• 序列 \(A\) 是序列 \(S\) 的连续子序列当且仅当可以通过删除 \(S\) 的开头和结尾的若干元素（可以不删除）得到 \(A\\\)。\(\\\)为了强调合作，小 J 给了 \(n\) 个参与游戏的人 \(q\) 个任务，第 \(j\) 个任务需要这 \(n\) 个人进行一次游戏，在这次游戏里进行恰好 \(r_j\) 轮接龙，且最后一轮的接龙序列的最后一个元素恰好为 \(c_j\)。为了保证任务的可行性，小 J 请来你判断这 \(q\) 个任务是否可以完成的，即是否存在一个可能的游戏过程满足任务条件。

思路

注意到 \(r\le 100\) 说明这道题目可以用 DP 来实现。

定义 \(f_{i,j}\) 表示第 \(i\) 轮结束位置是 \(j\) 的方案数。

暴力转移每次查找上一次 \(j\) 出现的位置进行转移，那么这样做的时间复杂度是 \(O((\sum l_i)^2r)\)，肯定直接会 TLE。