标签：总结 环上 mathit 笛卡尔 基环树 序列 节点

一个图论，一个半数据结构。咱也不知道为啥这两个毫无关联的东西会放在一块。

---

基环树（环套树）

一些定义

• 基环树：一张有 \(N\) 个点和 \(N\) 条边的图，如果不保证连通的话，那么整张图是一张基环树森林。并且如果将环上的任意一条边去除，那么整棵基环树会成为一棵普通的树。
• 内向树：一棵所有节点出度为 \(1\) 的有向基环树，如图：
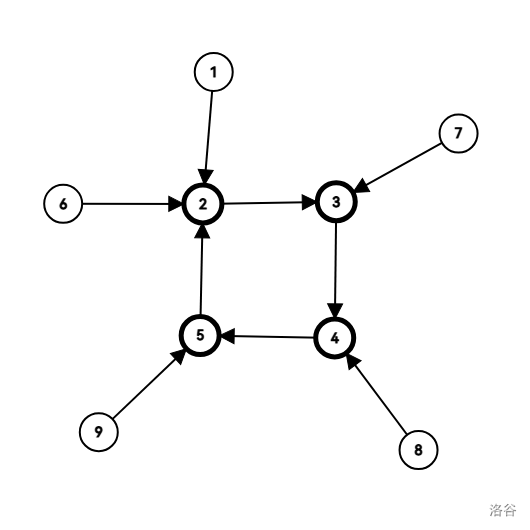
• 外向树：一棵所有节点入度为 \(1\) 的有向基环树，如图：

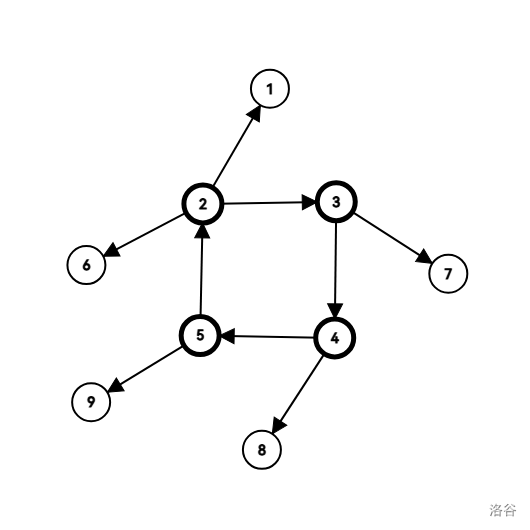
处理方法

基环树一般用于给普通的树上问题增加难度。

树形 DP

找到环，断开环上一边，使之成为普通的树，然后进行树形 DP。又因为断开了一条边，于是这条边连接的两个端点无法处理，所以通常需要进行两次树形 DP。

典型例题：P2607，P5022，创世纪。

环形 DP

找到环，由于环上每一点都相当于根节点引导一棵子树，于是将子树信息合并到环上点，于是基环树就变成了一个环，然后跑环形 DP。

典型例题：P4381，P3533。

找环

基环树就如上两种处理方法，但不论哪种，第一步都是找到环，下面看如何找环。

对于无向图

拓扑排序：可以很方便地找出环上所有节点。

void toposort() {
    queue<int> q;
    for (int i = 1; i <= n; i++) if (in[i] == 1) q.push(i);
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (auto vv : g[u]) {
            int v = vv.first, w = vv.second;
            if (in[v] > 1) {
                in[v]--;
                s[tr[v]] = max(s[tr[v]], dis[v] + dis[u] + w);
                dis[v] = max(dis[v], dis[u] + w);
                if (in[v] == 1) q.push(v);
            }
        }
    }
}

DFS：也可找出环上所有节点，在无向图上不如拓扑排序简洁。

void isring(int u, int fno) {
    if (ins[u]) {
        ring[u] = 1;
        for (int i = top; stk[i] != u; i--) ring[stk[i]] = 1;
        return;
    }
    if (vis[u]) return;
    vis[u] = 1;
    stk[++top] = u;
    ins[u] = 1;
    for (auto v : g[u]) if (v != fno) isring(v);
    --top;
    ins[u] = 0;
}

对于有向图

DFS：和无向图的 DFS 类似，不需像无向图一样判断父节点。

void isring(int u) {
    if (ins[u]) {
        ring[u] = 1;
        for (int i = top; stk[i] != u; i--) ring[stk[i]] = 1;
        return;
    }
    if (vis[u]) return;
    vis[u] = 1;
    stk[++top] = u;
    ins[u] = 1;
    for (auto v : g[u]) isring(v);
    --top;
    ins[u] = 0;
}

DFS 找出环上一点

有向图和无向图皆可用。如果有一个点 \(v\) 被两次访问，那么就存在环，且 \(v\) 是环上一点。代码很好写，以下代码仅供参考。

int check(int u) {
    vis[u] = 1;
    if (vis[fa[u]]) return fa[u];
    return check(fa[u]);
}

例 1 [ZJOI2008] 骑士

题意

骑士团有很多骑士，一些骑士之间相互有矛盾，每个骑士有且仅有一个他讨厌的骑士，且绝对不和自己讨厌的骑士一起出征。为了组成一个战斗力最大的军团，要求这个团内所有人都没有矛盾且战斗力最大。骑士按 \(1\sim n\) 编号，每个人有一个战斗力，军团的战斗力是所有骑士战斗力之和。

\(1\le n\le10^6\)，每人战斗力是不大于 \(10^6\) 的整数。

解析

本题和 P1352 没有上司的舞会 相似，但本题给出了一个基环树。考虑把 \(x\) 讨厌的人 \(y\) 设为 \(x\) 的父节点，形成一条有向边 \((y,x)\)，记为 \(\mathit{fa}(x)=y\)。用 DFS 找出环上一点 \(u\)，断开 \((\mathit{fa}(u),u)\) 使其成为两棵树，分别同 P1352 一样进行树形 DP。又考虑到 \(u\) 和 \(\mathit{fa}(u)\) 不可以都去，那么一定有一个人不去，所以在跑完两次树形 DP 后，只需取 \(\min(\mathit{dp}[u,0],\mathit{dp}[\mathit{fa}(u),0])\) 即可。

AC Code

例 2 [NOIP2018 提高组] 旅行

看到数据范围中的 \(m=n-1\) 和 \(m=n\)，就知道应该分类讨论。当年的 NOIP 这么良心，只考虑树的情况就能有 60pts。

\(\boldsymbol{m=n-1}\)

此时整张图为一棵树，因为题目要求路径序列字典序最小，所以对邻接表进行从小到大排序，从节点 \(1\) 开始 DFS 完整棵树即可。此时的路径序列字典序一定是最小的。

\(\boldsymbol{m=n}\)

此时整张图为一棵基环树。看到数据范围：\(n\le5000\)，允许 \(O(n^2)\) 的复杂度，于是我们就暴力找环、删边，把环上的所有边都删一遍，取字典序最小的路径序列即可。DFS 里稍加一些剪枝，妥妥过掉这道题。

当然有更高级的 \(O(n\log n)\) 的算法，对标此题加强版。

AC Code

例 3 [IOI2008] Island

题意

给定一个基环树森林，求每个基环树的最长链长度。

解析

08 年的 IOI 啊。

题意如此直接。

从此题开始难度骤升，让你认识到基环树的魅力。

回归题目。所谓 “最长链”，让你想到了什么？没错，树的直径。

但是树的直径只是针对树，而本题给的是基环树。

那么基环树无非多了什么？一个环。所以有两种情况。

1. 最长链两端点全部位于环上同一点的子树内。换句话说，不经过环。那么此时的最长链直接就是该子树的直径。
2. 最长链两端点位于不同子树。那么此时的最长链 = 两个端点在各自子树中到根节点的距离 + 环上两点的最短距离。

思路就以上这些。打到代码上，我们需要维护：

• \(\mathit{tr}(i)\)，表示节点 \(i\) 位于哪棵基环树，用于遍历森林；
• \(\mathit{dis}(i)\)，表示当前子树中从节点 \(i\) 出发向下的最长距离，用于查询环上节点到最长链端点的距离（相当于将子树信息合并到环上节点）；
• \(s(i)\)，表示第 \(i\) 棵基环树在情况一下的最长链，其实就是每棵子树的直径取最大值，用于分类讨论；
• \(d(i)\)，表示从环上任意一点到环上节点 \(i\) 的距离，其实是前缀和数组：用 \(d(j)-d(i)\) 表示 \(i,j\) 两点在环上的距离。
• 在实际实现中，最终我们将基环树合并为一个环，所以我们用一个 \(f(i)\) 同样表示 \(d(i)\) 的维护内容，只不过这里的 \(\boldsymbol i\) 仅限于环上节点，即将环上节点重新编号为 \(\boldsymbol{1\dots \textbf{\mathit{len}}}\)，\(\textbf{\mathit{len}}\) 为环长。

环形 DP 的时候需要单调队列维护，具体不讲了。

然后，梳理一遍思路：

1. 读入。
2. 一个 DFS 跑出所有基环树，对不同基环树上的点作标记。
3. 拓扑排序求出每棵基环树的环，顺便可以求出 \(s\) 和 \(\mathit{dis}\)。
4. 对于每个基环树跑一遍环形 DP，其中用到单调队列解决。

AC Code

例 4 [POI2012] RAN-Rendezvous

题解在此。

例 5 创世纪

题意

上帝手中有着 \(n\) 种被称作 “世界元素” 的东西，现在他要把它们中的一部分投放到一个新的空间中去以建造世界。每种世界元素都可以限制另外一种世界元素，所以说上帝希望所有被投放的世界元素都有至少一个没有被投放的世界元素能够限制它，这样上帝就可以保持对世界的控制。

上帝希望知道他最多可以投放多少种世界元素。\(n\le10^6\)。

题解

这里解子挺多的，思路基本就是这个思路，不再多说了。

笛卡尔树

什么是笛卡尔树？

我们先回顾 Treap 树，它的每个节点有两个属性：键值和优先级。笛卡尔树是一种特殊、简化的 Treap，它的每个节点的键值预先给定，但是优先级或预先给定、或随机生成。

笛卡尔树主要用于处理一个确定的序列，序列中的数有两个属性：在序列中的位置和数值。把位置看作键值，数值看作优先级，构造出来的笛卡尔树符合 Treap 的特征，即：

1. 以每个数的位置（记作 \(k\)）为键值，它是一棵 BST。
2. 把数值（记作 \(w\)）看作优先级，它是一个堆。

性质

除了以上的性质，笛卡尔树还有其他的一些有用的性质。

1. 对于一棵笛卡尔树，它的中序遍历就是原序列。
   由 Treap 的性质不难证明。
2. 在原序列中的区间 \(\boldsymbol{[l,r]}\) 的最小值（或最大值），就是这个序列的笛卡尔树上 \(\boldsymbol l\) 和 \(\boldsymbol r\) 的 LCA。
   因为 \(l\) 和 \(r\) 的 LCA 一定在区间 \([l,r]\) 中，且在整个区间中深度最小。因为笛卡尔树关于 \(w\) 是堆，如果是小根堆则 \([l,r]\) 的最小值是 LCA，如果是大根堆则最大值是 LCA。
3. 对于一个序列，如果其 \(\boldsymbol{k,w}\) 均互不重复，则其所构建的笛卡尔树是唯一的。
   因为 \(k\) 互不重复，所以能构建出唯一无根 BST。又因为笛卡尔树关于 \(w\) 是堆，所以 \(w\) 最小/最大的节点为根。因为 \(w\) 互不重复，所以根确定，所以笛卡尔树确定。

建树

如果用 Treap 的建树方法，逐一加入节点，再通过 FHQ 维护，时间复杂度为 \(O(N\log N)\)。

笛卡尔树是简化的 Treap，它所有节点均预先给定，所以有 \(O(N)\) 的建树方法。

由于所有节点均预先给定，每次插入新的节点，横向的位置是固定的，新的点总是插入最右边，而且需要调整的是纵向位置，所以只需考虑 “最右链”，可以用单调栈维护。在最右链上，从上一个插入的点开始，若栈顶节点的 \(w\) 值比当前大/小，就将其放在当前节点的左子树，否则直接将当前节点接在栈顶节点的右子树上。如图：

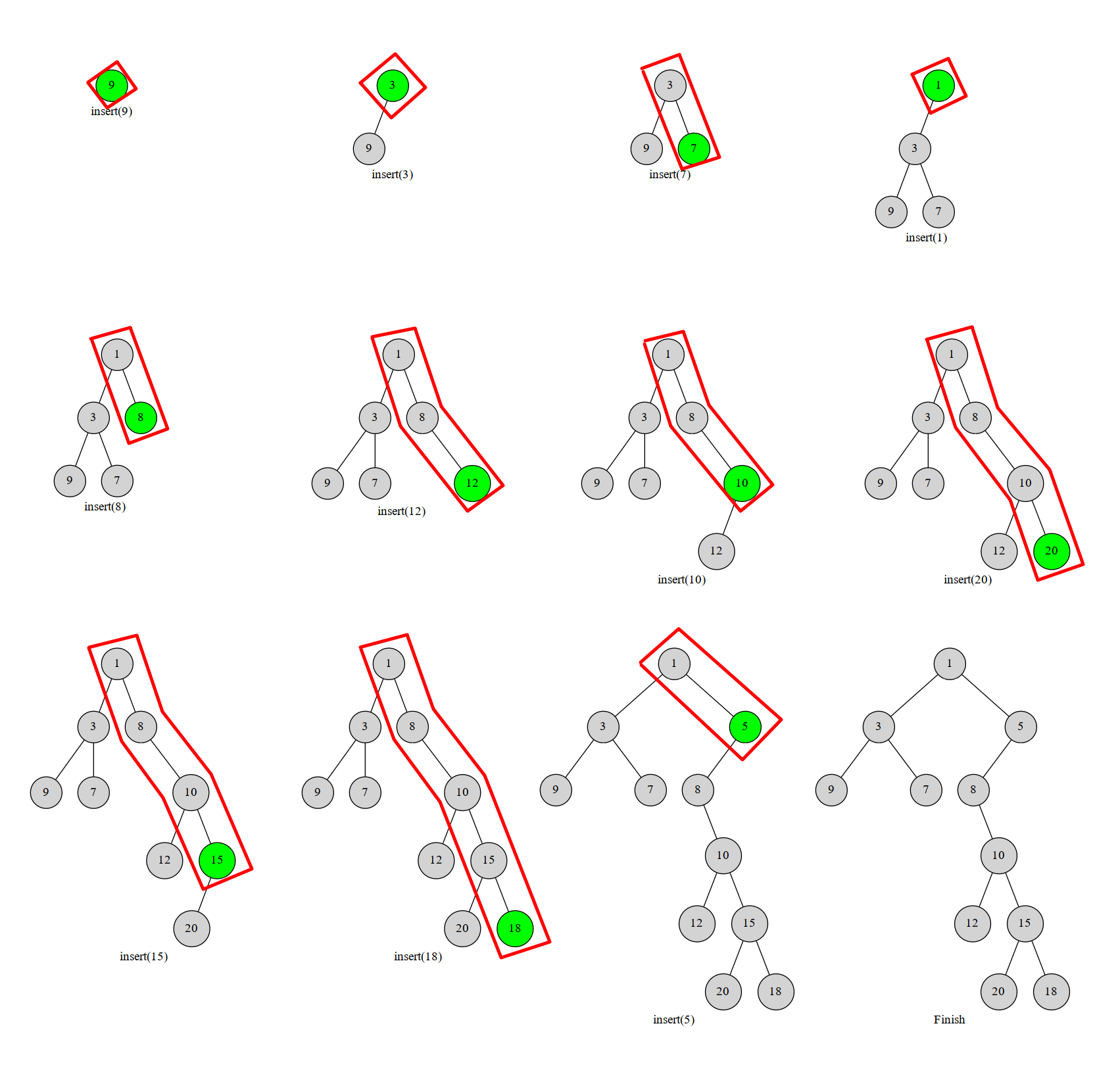
void insert(int k, int w) {
    while (!st.empty() && w < a[st.top()].second) {
        ls[k] = st.top();
        st.pop();
    }
    if (!st.empty()) rs[st.top()] = k;
    st.push(k);
}

维护笛卡尔树时，只需维护一个 \(\mathit{ls}(i)\) 表示节点 \(i\) 的左儿子，\(\mathit{rs}(i)\) 表示节点 \(i\) 的右儿子，外加一个栈用来建树即可。

例 1 [TJOI2011] 树的序

题目相当于给了 \(k\)，我们将 \(k\) 维护成一棵 BST。因为必须先加父亲节点再加儿子节点，又要求字典序最小，所以父亲的加入顺序应比儿子小，所以顺序构成一个堆。所以这是一棵标准的笛卡尔树，题目给定 \(k\)，输入顺序为 \(w\)。建成一棵笛卡尔树，答案就是 \(w\) 的先序遍历。

AC Code

例 2 RMQ Similar Sequence

题意

定义 \(\operatorname{RMQ}(A,l,r)\) 表示序列 \(A\) 中 \([l,r]\) 的区间最大值的 \(i\)。

两个序列 \(A\) 和 \(B\) 被称作是 “RMQ 相似的” 当且仅当 \(\forall1\le l\le r\le n\)，\(\operatorname{RMQ}(A,l,r)=\operatorname{RMQ}(B,l,r)\)。

给定一个序列 \(A\)，假设一个与 \(A\) RMQ 相似的序列 \(B=\{b_1,b_2,\dots,b_n\}\) 的权值为 \(\sum_{i=1}^nb_i\)，否则序列 \(B\) 的权值为 \(0\)。如果序列 \(B\) 中的每个元素都是区间 \([0,1]\) 之间的一个随机实数，求序列 \(B\) 的期望权值。

题解 from @Dyc780511

因为序列 \(A,B\) 的所有子区间的 RMQ 相同，那么序列 \(A,B\) 的笛卡尔树应该是同构的。又因为序列 \(B\) 中的元素都是区间 \([0,1]\) 内的实数，所以序列 \(B\) 内有重复元素的概率无限趋近于 \(0\)。我们假设序列 \(B\) 中没有重复元素，那么根据性质 3，序列 \(B\) 的笛卡尔树应该是唯一的。接着考虑对于每一个序列 \(B\) 的笛卡尔树与序列 \(A\) 的笛卡尔树同构的概率。因为数字从左往右的顺序不变，根据性质 1，只要确定了根节点，那么两边的元素集合一定相等，所以只要所有子树的根节点都相同，那么两个笛卡尔树就是同构的。设以 \(i\) 为根节点的子树大小为 \(\mathit{siz}_i\)，那么笛卡尔树同构的概率为 \(\dfrac{1}{\prod_{i=1}^n\mathit{siz}_i}\)。而序列 \(B\) 内每一个元素的期望都是 \(1/2\)，所以符合条件序列 \(B\) 的权值期望为 \(n/2\)，所以序列 \(B\) 的权值期望为 \(\dfrac{n}{2\times\prod_{i=1}^n\mathit{siz}_i}\)。

AC Code

例 3 [COCI2008-2009#4] PERIODNI

题解在此。

例 4 Moles

一看就知道是笛卡尔树。题目中给的顺序相当于 \(k\)，值相当于 \(w\)，按照题意构建笛卡尔树。所谓 “记录性别”，不过是对笛卡尔树进行 DFS，记录欧拉序即可。由于笛卡尔树的 \(w\) 相当于一个小根堆，所以是符合题意的。最后对你记录的欧拉序和题目给定匹配串进行匹配，Hash 和 KMP 均可。

部分人会认为此题卡 Hash，实际上是不卡的，完全是你自己打炸了，请自行检查。比如，请检查你的欧拉序字符数组是否开了二倍。

AC Code

例 5 Kcats

题解 from @Dyc780511

考虑到 \(a_i\) 本质上是最后的笛卡尔树上，第 \(i\) 个节点的所有祖先中 \(k\) 值比自己小的节点的数量。接着考虑区间 DP，令 \(f(l,r,d)\) 表示区间 \([l,r]\) 所对应的笛卡尔树的根节点的祖先中有 \(d\) 个 \(k\) 值比自己小。那么它的左儿子节点，即区间 \([l,\mathit{rt}]\) 的根节点的有贡献的祖先节点一定和它的祖先节点是一样的。但是它的右儿子节点，即区间 \((\mathit{rt},r]\) 的根节点不仅有它有的祖先节点，还包含它本身。因为笛卡尔树满足小根堆，所以它的左子树一定比他大且按顺序排列，因此数字的组合可能为 \(\dbinom{j-i}{k-i}\)。转移方程为：

\[f(i,j,d)=\sum_{k=i}^{j} \begin{cases} \displaystyle\sum_{d=a_k}f(i,k-1,d)\times f(k+1,j,d+1)\times\binom{j-i}{k-i}&a_k\ne-1 \\ \displaystyle\sum_{d=1}^{n}f(i,k-1,d)\times f(k+1,j,d+1)\times\binom{j-1}{k-i}&a_k=-1 \end{cases} \]

AC Code

标签：总结,环上,mathit,笛卡尔,基环树,序列,节点
From： https://www.cnblogs.com/laoshan-plus/p/18565810