专题:分段函数+函数性质 \(\qquad \qquad\) 题型:新定义问题 \(\qquad \qquad\) 难度系数:★★★
【题目】
所谓图形\(D\)完全覆盖曲线\(G\)是指\(G\)中的每一个点都落在\(D\)的内部或边界,现用一个有两个顶点在\(x\)轴上的矩形区域完全覆盖函数\(f(x)=\left\{\begin{array}{l} -4 x(x-1), 0 \leq x \leq 1 \\ 4 x(x+1),-1 \leq x<0 \end{array}\right.\),\(x\in\left[-1,1\right]\)的图像,则这个矩形对角线长的最小值为( ).
A.\(\dfrac{256}{205}\) \(\qquad \qquad\) B.\(\dfrac{256}{225}\) \(\qquad \qquad\) C.\(\dfrac{289}{240}\) \(\qquad \qquad\) D.\(\dfrac{289}{120}\)
【详解】
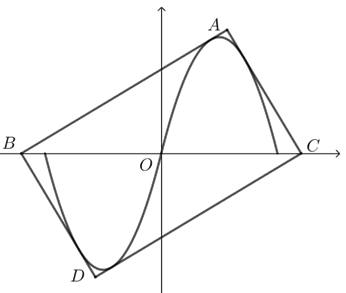
依题意,可知所求矩形也是关于原点对称.
设矩形在\(x\)轴上方的点为\(A\),\(x\)轴上两点分别为\(B\)、\(C\)(\(B\)在\(C\)左侧).
由对称性:只考虑\(y>0\),
利用对称性,减少讨论范围,减少计算.
依题意可知,当矩形的对角线\(|BC|\)取到最小值时,矩形四边均与\(f\left(x\right)\)的图像相切.
还是由于对称性,对角线\(\left|BC\right|=2\left|OB\right|=-2x_B\),即求出点的横坐标便可.
设直线\(AB:y=k_1x+m_1\),\(x_B=-\dfrac{m_1}{k_1} \)
联立方程\(\left\{\begin{array}{c} y=k_1 x+m_1 \\ y=-4 x(x-1) \end{array}\right.\)得\(4x^2+\left(k_1-4\right)x+m_1=0\),
由于相切则\(\Delta=0\Rightarrow\left(k_1-4\right)^2-4\cdot4\cdot m_1=0\Rightarrow m_1=\dfrac{\left(k_1-4\right)^2}{16}\),
利用高二学的导数,会简单些.
此时\(x_B=-\dfrac{m_1}{k_1}=-\dfrac{\left(k_1-4\right)^2}{16k_1}\), 求\(k_1\)便可得出答案.
设直线设直线\(AC:y=k_2x+m_2\),
同理可得\(x_C=-\dfrac{m_2}{k_2}=-\dfrac{\left(k_2-4\right)^2}{16k_2}\),
由于点\(B\)与点\(C\)关于原点对称,所以\(x_B+x_C=0\),
即\(-\dfrac{\left(k_1-4\right)^2}{16k_1}+-\dfrac{\left(k_2-4\right)^2}{16k_2}=0\Rightarrow k_1+k_2=-\dfrac{16}{15}\),
由于\(AB\bot AC\),则有\(k_1k_2=-1\),
直线\(l_1\bot l_2\),则\(k_1k_2=-1\);直线\(l_1||l_2\),则\(k_1=k_2\).
又\(k_1+k_2=-\dfrac{16}{15}\),
所以\(k_1\),\(k_2\)是方程\(k^2+\dfrac{16}{15}k-1=0\)的两个实数根,
解得\(k_1=\dfrac{3}{5},k_2=-\dfrac{5}{3}.\)
所以矩形对角线的最小值为\(\left|BC\right|=2\left|OB\right|=-2x_B=-2\left[-\dfrac{\left(k_1-4\right)^2}{16k_1}\right]=\dfrac{289}{120}\).
故选:\(D\).
总结
- 对于涉及图象,多数形结合,注意观察图像的特点,比如点\(B\)与点\(C\)关于原点对称得\(x_B+x_C=0\)是关键;
- 对于函数有中心对称或轴对称,均可讨论一边情况便可;在运算中,遇到同理问题,要避免重复计算;
- 充分利用已知条件,比如题中的矩形,前面用了对称性只用了“平行四边形”的性质,那容易想到要用上\(AB\bot AC\)或对角线相等;
- 对问题的分析,要懂得层层“转化”:要求什么只需求什么,由难化简;
- 本题还是其他想法,比如\(AB\bot AC\)的利用能否求出点\(A\)的坐标呢?不用\(k_1k_2=-1\),用射影定理是否可行?一题多解有助于思维的提高!