炼石计划 10 月 04 日 NOIP 模拟赛 #8【补题】 - 比赛 - 梦熊联盟 (mna.wang)
复盘
T1 有种 div.2 B 的风格,没秒,想看题。
T2。只判是否无解?\(k \le 100\)?把 \(200\) 个关键连通块拿出来建图跑传递闭包不就做完了。
一遍过大样例?简直不可思议,但还是把 T2 关了吧。
用分析 CF 题的方式分析 T1。发现两个隔着比较远的数如果能合并就以为着它们中间隔着的数一定是奇数个。所以它们的下标一定同奇偶。
所以把奇数位置的正数取出来,或把偶数位置的正数取出来,这不就是第一问?第二问的答案难道不是固定?难道不是做完了?
细节有点多,打不是很多。开场 40 分钟切掉。
对拍启动。发现第一个点就挂。于是调暴力程序。Two Hundred years later...
T3 T4 好复杂。正解肯定不会的啦。暴力启动。
最终预期 \(100+100+20+20=240\),实际 T4 爆零了。原因未知。话说为什么比较复杂的题的爆搜总写不对呢???
总结
好的:
- 挂分不多(这也算优点???)
- 比较稳,前两题没有挂分。
不足:
- 写对拍时过于不仔细,暴力程序挂了好多次,浪费了很多时间。
- 爆搜经常写不对。
知识点
- T1:贪心;
- T2:搜索,图论,传递闭包;
- T3:归并排序,线段树(正解用到线段树但我还没补出来)。
题解
A. 养蛊神器
首先判掉,如果全是负数,那么第一问的答案一定是 \(\max a_i\)。对于第二问枚举所有最大值,然后算将两边全部清空的步数即可。将长 \(x\) 的全部清空的最小步数是 \(\lfloor x / 2 \rfloor+1\)。
操作二相当于选择一个长度为 \(3\) 的区间,将其合并为两个端点的和。
注意到若区间长度为 \(5\),那么我们可以先对中间三个元素做一次操作,然后将整个区间再做一次操作,也能做到上面的效果——将整个区间合并成两个端点的和。同理,只要长度为大于 \(1\) 的奇数,都能完成这个操作。
所以我们考虑最终答案的可能的组成,即答案可能是哪些数的加和。不难发现,令最终答案为 \(a_{i_1}+a_{i_2}+\dots+a_{i_k}\)(\(i_1<i_2<\dots<i_k\)),那么这个答案合法的充要条件是 \(i_1 \equiv i_2 \equiv \dots \equiv i_k \pmod 2\)。
所以我们可以全选奇数位上的正数,或全选偶数位上的正数。这两者的较大值就是第一问。这里我们不妨将 \(0\) 也视作正数。
对于第二问,不难发现将 \([i_j+1,i_{j+1}-1]\)(\(1 \le j < k\))内的数删掉的方案是唯一的,其步数为 \((i_{j+1}-i_j)/2\)。两侧单独处理即可,与上面全是负数的特判类似。
B. 导航神器
首先 flood fill 求出每个点所在的连通块。如果有一个传送门的起点在连通块-\(x\) 内,终点在连通块-\(y\) 内,那么我们连一条边 \(x \to y\)。然后跑传递闭包即可。
但是连通块数很大,也即图中点数很大,直接跑肯定不行。注意到传送门的数量 \(\le 100\),这意味着图中度不为 \(0\) 的点至多 \(200\) 个。所以只对这 \(200\) 个点跑传递闭包,查询时分讨一下是否是关键点即可。
C. 扰乱神器
还不会,但是会了 Subtask3,即将每个块都翻转。
注意到,将这 \(2^q\) 个长 \(2^{n-q}\) 的块翻转,相当于 \(\operatorname{swap}(a_i, a_{i \oplus (2^{n-q}-1)})\),即将 \(i\) 的后 \(n-q\) 位翻转。考虑将所有的 \(i\) 都执行这样的操作后,逆序对会发生什么变化。
不妨将整个序列做一遍归并排序(或者说画一颗递归树)。例如当 \(n = 3\):
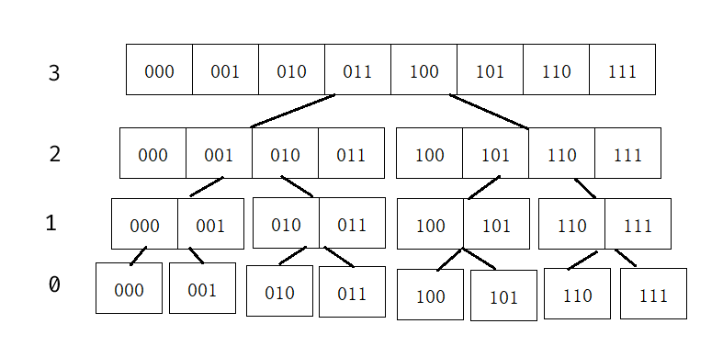
不难发现,这颗树上的第 \(d\) 层中,每一个区间所对应的点,在二进制视角下,从第 \(d\) 位到最高位都全部相同。
所以如果我们要把所有 \(i\) 的后 \(n-q\) 位都翻转,就意味着这棵树中,把所有层数 \(\le d\) 的节点的左右儿子互换。例如当 \(n - q = 2\) 时上图变为:
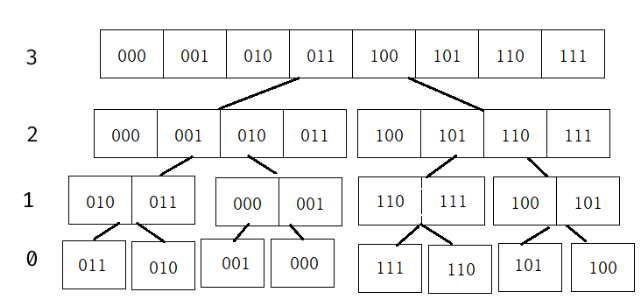
然后考虑如何处理逆序对。我们令 \(f(d)\) 表示有多少对逆序对 \((i,j)\),使得存在一个层数为 \(d\) 的点,使得其左儿子包含 \(i\),右儿子包含 \(j\)(实际上类似 cdq 分治,考虑每个层数为 \(d\) 的点里,跨过中点的对的贡献)。\(g(d)\) 同理表示顺序对。那么将层数为 \(d\) 的所有点的左右儿子交换后,其效果等价于 \(\operatorname{swap}(f(d),g(d))\)。所以预处理 \(f,d\) 即可。显然答案为 \(\sum f(d)\)。
标签:闭包,连通,le,10.18,层数,100,正数,模拟 From: https://www.cnblogs.com/2huk/p/18474874