Problem Link

[HNOI2005] 数三角形

题意

输入一个大三角形的各个边存在情况，输出里面有多少个正三角形。

Solution

简单暴力即可，用 \(4\) 个数组维护每条边能延伸的最大长度，然后逐个判断三角形是否可行即可。

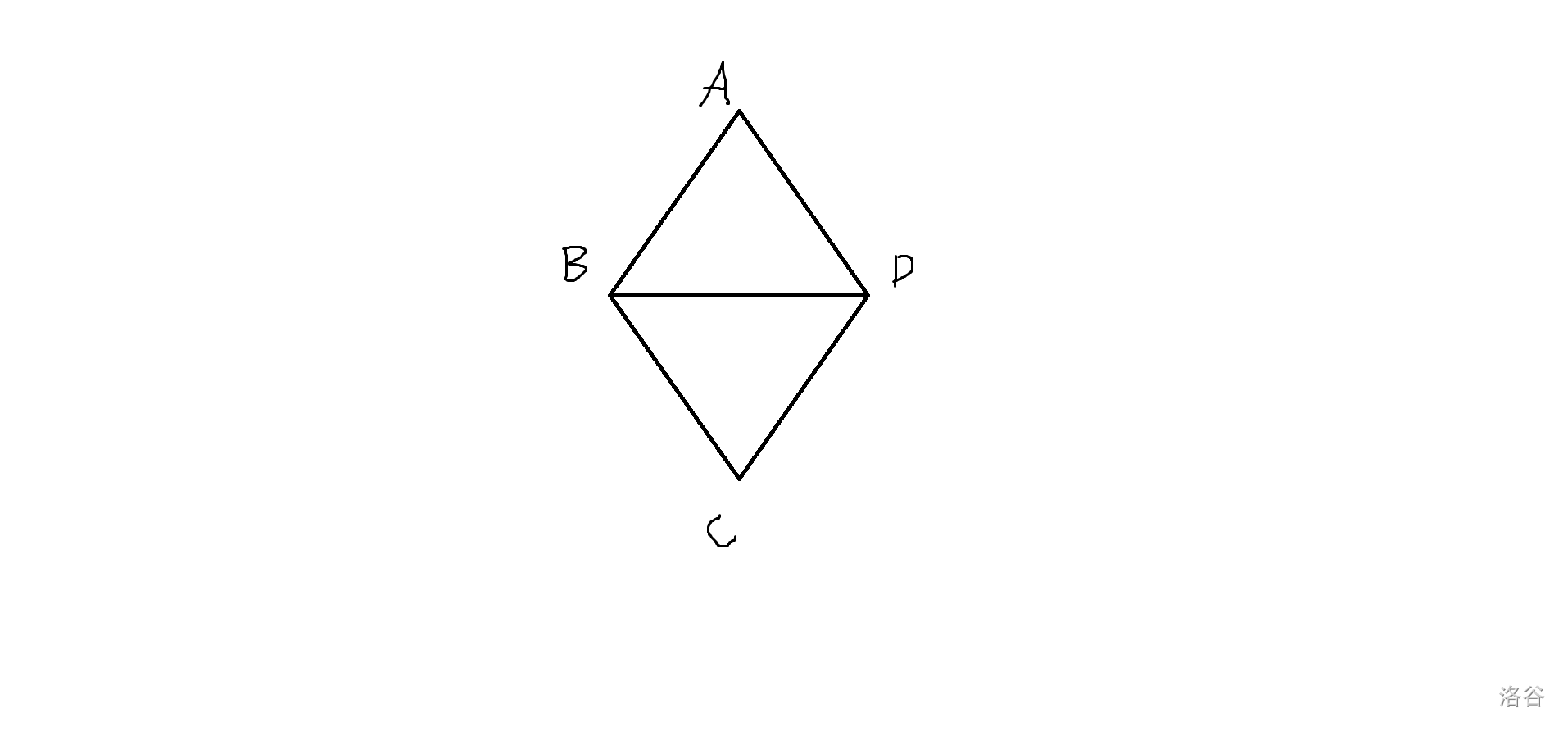
如图，l_upper 维护左端点向上（即 $\ell_{BA} $），l_lower 维护左端点向下（即 $\ell_{BC} $），r_upper 维护右端点向上（即 $\ell_{DA} $），r_lower 维护右端点向下（即 $\ell_{DC} $。

Code

//wriiten by Naught
#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
#define Maxn 1005
#define fo(i, l, r) for(int i = l; i <= r; ++i)
#define fr(i, r, l) for(int i = l; i >= r; --i)
#define getchar()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21], *p1 = buf, *p2 = buf;
inline int read(int x=0, bool f=0, char c=getchar()) {for(;!isdigit(c);c=getchar()) f^=!(c^45);for(;isdigit(c);c=getchar()) x=(x<<1)+(x<<3)+(c^48);return f?-x:x;}

struct Trangle
{
    bool l, r, d;
}a[Maxn][Maxn];

int n, ans, l_upper[Maxn][Maxn], r_upper[Maxn][Maxn], l_lower[Maxn][Maxn], r_lower[Maxn][Maxn];

int main()
{
    n = read();
    fo(i, 1, n) fo(j, 1, i) a[i][j] = {(bool)read(), (bool)read(), (bool)read()};
    fo(i, 1, n) fo(j, 1, i) if(a[i][j].l) l_upper[i][j] = l_upper[i-1][j]+1;
    fo(i, 1, n) fo(j, 1, i) if(a[i][j].r) r_upper[i][j] = r_upper[i-1][j-1]+1;
    fr(i, 1, n) fo(j, 1, n) if(a[i+1][j].r) l_lower[i][j] = l_lower[i+1][j+1]+1;
    fr(i, 1, n) fo(j, 1, i) if(a[i+1][j+1].l) r_lower[i][j] = r_lower[i+1][j]+1;
    fo(i, 1, n) fo(j, 1, n)
        for(int k = j; k <= n && a[i][k].d && k-j+1 <= l_upper[i][j]; ++k) 
            ans += (k-j+1) <= r_upper[i][k];
    fo(i, 1, n) fo(j, 1, n)
        for(int k = j; k <= n && a[i][k].d && k-j+1 <= l_lower[i][j]; ++k)
            ans += (k-j+1) <= r_lower[i][k];
    printf("%d", ans);
    return 0;
}