题目:
在约10000m高空的某边长160km的正方形区域内,经常有若干架飞机作水平飞行。区域内每架飞机的位置和速度向量均由计算机记录其数据,以便进行飞行管理。当一架欲进入该区域的飞机到达区域边缘时,记录其数据后,要立即计算并判断是否会与区域内的飞机发生碰撞。如果会碰撞,则应计算如何调整各架(包括新进入的)飞机飞行的方向角,以避免碰撞。现假定条件如下:
(1)不碰撞的标准为任意两架飞机的距离大于8km。
(2)飞机飞行方向角调整的幅度不应超过30°。
(3)所有飞机飞行速度均为800km/h。
(4)进入该区域的飞机在到达区域边缘时,与区域内飞机的距离应在60km以上。
(5)最多需考虑6架飞机。
(6)不必考虑飞机离开此区域后的状况。
求解:
首先对模型进行假设:
- 假设区域内所有飞机都沿水平直线正常飞行(不考虑意外坠毁等情况)。
- 若飞机需要进行飞行角度调整,则假定在角度调整过程中飞机速度不变。
- 假设新的飞机进入区域边缘时,区域内其他飞机的飞行方向和角度都合适。
- 假设每架飞机最多只改变一次飞行角度。
- 飞机进入边缘时就对飞机的方向角进行调整。
- 不考虑天气状况(不稳定气流,暴雨等)对飞机飞行造成的影响。
然后假设一些符号方便我们分析这个问题:

符号解释
每架飞机初始位置及初始角度见代码部分。
假设两架飞机先在 (x1,y1), (x2,y2) ,t时间后, \(x_i(t)=x_i(0)+vtcos\theta_i\) , \(y_i(t)=y_i(0)+vtcos\theta_i\) , \(\theta_i=\theta_i(0)+\Delta\theta_i\)
两飞机间的间距 \(d_{ij}=\sqrt{(x_i^2-x_j^2)+(y_i^2-y_j^2)}\) , 为方便计算,将其转化为 : \(d_{ij}^2=(x_i^2-x_j^2)+(y_i^2-y_j^2)\)
解模型
求导算critical point. 然后在临界点不相撞
以12两架飞机为例,借鉴b站大师兄数学建模的求导过程:

添加图片注释,不超过 140 字(可选)
由于需要每两架飞机间都不小于8m,所以可得到非线性规划
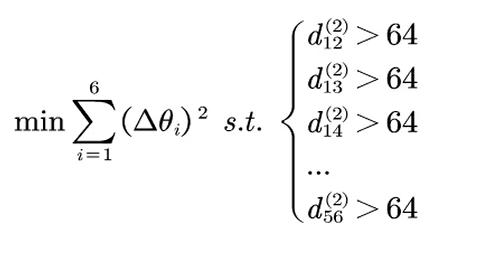
添加图片注释,不超过 140 字(可选)
或者 直接按时间模拟,每个时间点都不相撞,见代码部分
代码部分
% 目标函数
function y=hwf1(seta)
for i=1:6
y=seta(i).^2;
end
end
% 主程序
clear,clc;
x0=zeros(1,6);%初值限定
lb=zeros(1,6);%下界
ub=[(pi/6).^2 (pi/6).^2 (pi/6).^2 (pi/6).^2 (pi/6).^2 (pi/6).^2];%上界
[x,fval]=fmincon(@hwf1,x0,[],[],[],[],lb,ub,@hwf2)
% 非线性约束
function [c,ceq]=hwf2(seta)
% m,n,seta为初始位置(x, y)及初始角度
m=[150 85 150 145 130 0];
n=[140 85 155 50 150 0];
seta0 = [243 236 220.5 159 230 52]*pi/180;
c=[];x=[];y=[];
cosTheta=cos(seta0+seta);sinTheta=sin(seta0+seta);
for t=0:0.001:160*sqrt(2)/800 %按时间一直向下模拟,直到飞出该限制区
for i=1:length(m)
for j=i+1:length(m)
c=[c 64-((m(i)-m(j)+800*t*(cosTheta(i)-cosTheta(j)))^2+(n(i)-n(j)+800*t*(sinTheta(i)-sinTheta(j)))^2)];
end
end
end
ceq=0;
end