[WC2013] 糖果公园

题目描述

Candyland 有一座糖果公园，公园里不仅有美丽的风景、好玩的游乐项目，还有许多免费糖果的发放点，这引来了许多贪吃的小朋友来糖果公园游玩。

糖果公园的结构十分奇特，它由 \(n\) 个游览点构成，每个游览点都有一个糖果发放处，我们可以依次将游览点编号为 \(1\) 至 \(n\)。有 \(n - 1\) 条双向道路连接着这些游览点，并且整个糖果公园都是连通的，即从任何一个游览点出发都可以通过这些道路到达公园里的所有其它游览点。

糖果公园所发放的糖果种类非常丰富，总共有 \(m\) 种，它们的编号依次为 \(1\) 至 \(m\)。每一个糖果发放处都只发放某种特定的糖果，我们用 \(C_i\) 来表示 \(i\) 号游览点的糖果。

来到公园里游玩的游客都不喜欢走回头路，他们总是从某个特定的游览点出发前往另一个特定的游览点，并游览途中的景点，这条路线一定是唯一的。他们经过每个游览点，都可以品尝到一颗对应种类的糖果。

大家对不同类型糖果的喜爱程度都不尽相同。 根据游客们的反馈打分，我们得到了糖果的美味指数， 第 \(i\) 种糖果的美味指数为 \(V_i\)。另外，如果一位游客反复地品尝同一种类的糖果，他肯定会觉得有一些腻。根据量化统计，我们得到了游客第 \(i\) 次品尝某类糖果的新奇指数 \(W_i\)。如果一位游客第 \(i\) 次品尝第 \(j\) 种糖果，那么他的愉悦指数 \(H\) 将会增加对应的美味指数与新奇指数的乘积，即 \(V_j \times W_i\)。这位游客游览公园的愉悦指数最终将是这些乘积的和。

当然，公园中每个糖果发放点所发放的糖果种类不一定是一成不变的。有时，一些糖果点所发放的糖果种类可能会更改（也只会是 \(m\) 种中的一种），这样的目的是能够让游客们总是感受到惊喜。

糖果公园的工作人员小 A 接到了一个任务，那就是根据公园最近的数据统计出每位游客游玩公园的愉悦指数。但数学不好的小 A 一看到密密麻麻的数字就觉得头晕，作为小 A 最好的朋友，你决定帮他一把。

输入格式

从文件 park.in 中读入数据。

第一行包含三个正整数 \(n, m, q\)， 分别表示游览点个数、 糖果种类数和操作次数。

第二行包含 \(m\) 个正整数 \(V_1, V_2, \ldots, V_m\)。

第三行包含 \(n\) 个正整数 \(W_1, W_2, \ldots, W_n\)。

第四行到第 \(n + 2\) 行，每行包含两个正整数 \(A_i, B_i\)，表示这两个游览点之间有路径可以直接到达。

第 \(n + 3\) 行包含 \(n\) 个正整数 \(C_1, C_2, \ldots, C_n\)。

接下来 \(q\) 行， 每行包含三个整数 \(Type, x, y\)，表示一次操作：

• 若 \(Type\) 为 \(0\)，则 \(1 \leq x \leq n\)， \(1 \leq y \leq m\)，表示将编号为 \(x\) 的游览点发放的糖果类型改为 \(y\)；
• 若 \(Type\) 为 \(1\)，则 \(1 \leq x, y \leq n\)，表示对出发点为 \(x\)，终止点为 \(y\) 的路线询问愉悦指数。

输出格式

输出到文件 park.out 中。

按照输入的先后顺序，对于每个 \(Type\) 为 \(1\) 的操作输出一行，用一个正整数表示答案。

样例 #1

样例输入 #1

4 3 5
1 9 2
7 6 5 1
2 3
3 1
3 4
1 2 3 2
1 1 2
1 4 2
0 2 1
1 1 2
1 4 2

样例输出 #1

84
131
27
84

提示

【样例解释】

我们分别用

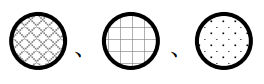
代表 \(C_i\) 为 \(1\)、 \(2\)、 \(3\) 的节点，在修改之前：

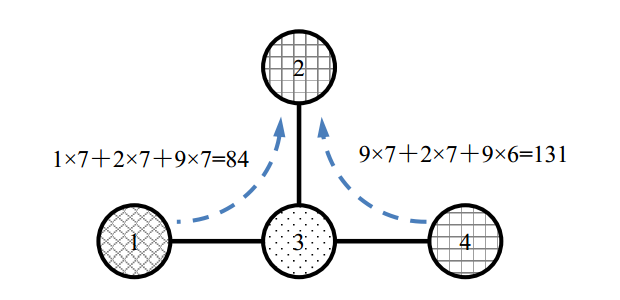
在将 \(C_2\) 修改为 \(1\) 之后：

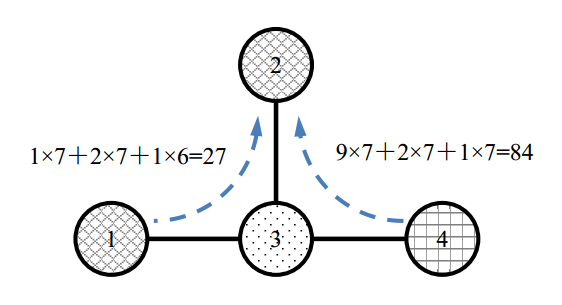
【数据规模与约定】

对于所有的数据： \(1 \leq V_i, W_i \leq 10^6\)，\(1 \leq A_i, B_i \leq n\)， \(1 \leq C_i \leq m\)， \(W_1, W_2, \ldots, W_n\) 是非递增序列，即对任意 \(1 < i \leq n\)， 满足 \(W_i \le W_{i-1}\)。

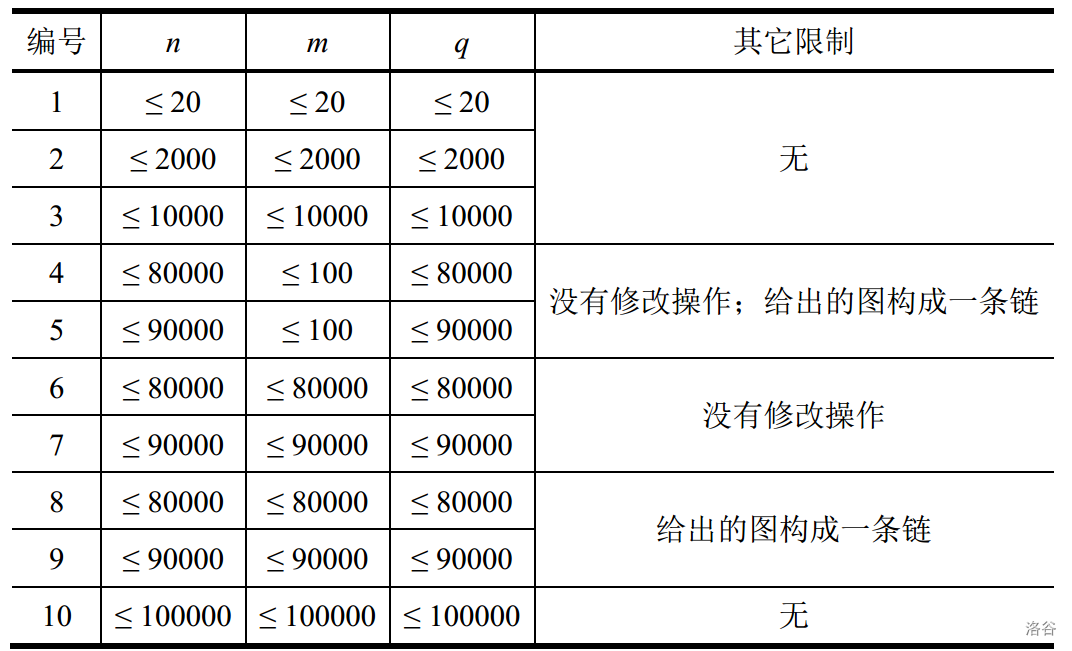
其它的限制条件如下表所示：

普通带修莫队,不太卡常数,TLE多半程序问题

时间复杂度 约 O(n^1.3)

#include<bits/stdc++.h>
using namespace std;

typedef __int128 i128;
typedef long long ll;
//#define int long long 
int read() {
	int res=0;char c=getchar();
	while(!isdigit(c)) c=getchar();
	while(isdigit(c)) 
		res=(res<<1)+(res<<3)+(c^48),c=getchar();
	return res;
}
const int N=2e5+7; 
int n,m,q,len;
int cq,cp;//询问次数  修改次数 
int a[N];
int v[N],w[N],col[N];
ll res,ans[N];
struct Q{
	int id,l,r,x,y,t;
    inline bool operator<(const Q b)const{
        if(x^b.x)return x<b.x;
        if(y^b.y)return x&1?y<b.y:y>b.y;
        return t<b.t;
    }
}q1[N];
struct C{
	int x,y;
}q2[N];
int cnt[N],vis[N];


int head[N],ne[N],to[N],idx;


int fa[N],top[N],dep[N],siz[N],son[N],pos[N],dfn;


inline void add(int u,int v){
	to[++idx]=v;
	ne[idx]=head[u];
	head[u]=idx;
}

/*-----------------------图部分--------------------------*/

void dfs1(int u){
	siz[u]=1;
	dep[u]=dep[fa[u]]+1;
	for(int i=head[u];i;i=ne[i]){
		int v=to[i];
		if(v==fa[u]) continue ;
		fa[v]=u;
		dfs1(v);
		siz[u]+=siz[v];
		if(siz[v]>siz[son[u]]) son[u]=v;
	}
}
void dfs2(int u,int p){
	top[u]=p;
	a[++dfn]=u;
	pos[u]=dfn;//树上节点在序列中的下标 
	if(son[u]) dfs2(son[u],p);
	for(int i=head[u];i;i=ne[i]){
		int v=to[i];
		if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
	}
	a[++dfn]=u;//欧拉序(不同于dfn序,每个点在序列中出现两次,中间的节点就是子树)
}
inline int lca(int u,int v){//lca 
	for(;top[u]^top[v];dep[top[u]]>dep[top[v]]?u=fa[top[u]]:v=fa[top[v]]);
    return dep[u]<dep[v]?u:v;
}


/*-----------------------莫队部分--------------------------*/

inline void sol(int x){
	vis[x]^=1;
	if(vis[x]) res+=1ll*w[++cnt[col[x]]]*v[col[x]];
	else res-=1ll*w[cnt[col[x]]--]*v[col[x]];
}
inline void upd(int id){
	int u=q2[id].x,x=q2[id].y,y=col[u];
	if(vis[u]) res+=(ll)w[++cnt[x]]*v[x]-(ll) w[cnt[y]--]*v[y];//更改带来的贡献 
	q2[id].y=y,col[u]=x;//swap操作 
}

/*-----------------------主函数--------------------------*/

signed main() {
	n=read(),m=read(),q=read();
	for(int i=1;i<=m;++i) v[i]=read();
	for(int i=1;i<=n;++i) w[i]=read();
	for(int i=2;i<=n;++i){
		int u=read(),v=read();
		add(u,v),add(v,u);
	}
	for(int i=1;i<=n;++i) col[i]=read();
	dfs1(1),dfs2(1,1);
	int x,y,t;
	for(int i=1;i<=q;++i){
		x=read();
		if(x){
			x=read(),y=read();
			if(pos[x]>pos[y]) swap(x,y);
			q1[++cq]=(Q){cq,x,y,pos[x],pos[y],cp};
		}
		else{
			x=read(),y=read();
			q2[++cp]=(C){x,y};
		}
	}
	len=pow(n,0.67);
	for(int i=1;i<=cq;++i) 
		q1[i].x/=len,q1[i].y/=len;
	sort(q1+1,q1+1+cq);
	int lcur=pos[q1[1].l],rcur=pos[q1[1].l]-1,tcur=0;
	for(int i=1;i<=cq;++i){
		x=pos[q1[i].l],y=pos[q1[i].r],t=q1[i].t;
		while(lcur>x) sol(a[--lcur]);
		while(lcur<x) sol(a[lcur++]);
		while(rcur<y) sol(a[++rcur]);
		while(rcur>y) sol(a[rcur--]);
		while(tcur>t) upd(tcur--);
		while(tcur<t) upd(++tcur);
		
		int u=q1[i].l,v=q1[i].r;
		int p=lca(u,v);
		if(u!=p){//如果起点不是lca,贡献不会被计算的
		//例如序列12443321 询问4->3 也就是[3,5]  2节点不会被访问 
			sol(u);
			if(v!=p) sol(p);
		}
        ans[q1[i].id]=res;
        if(u!=p){
			sol(u);
			if(v!=p) sol(p);
		}
	}
	for(int i=1;i<=cq;++i)
		printf("%lld\n",ans[i]);
	return 0;
}