定义
树形 \(DP\),这个挺明显的,我认为 \(DP\) 让读者理解的最重要的一步是:定义。
所以我先详细说明 \(f\) 数组的定义,至于为什么这么定义后面再讲。
\(f_{u, type}\),其中 \(type=0,1,2\)
\(f_{u,0}\) 表示:在原森林中,以 \(u\) 为根节点的子树变成链的最小代价,其中 \(u\) 必须被炸掉。
\(f_{u,1}\) 表示:在原森林中,以 \(u\) 为根节点的子树变成链的最小代价,其中 \(u\) 必须不被炸掉,且 \(u\) 最多有一个儿子。
\(f_{u,2}\) 表示:在原森林中,以 \(u\) 为根节点的子树变成链的最小代价,其中 \(u\) 必须不被炸掉,且 \(u\) 最多有两个儿子。
为什么这样定义
首先,一个节点炸或者不炸,是会影响它向父亲节点转移的,所以必须分类:炸掉、不炸掉。
而一个点如果不被炸掉,那么它应该有几个儿子呢?可以一个都没有,所有儿子都被炸掉;可以有一个或者两个,对应链的情况。如果有超过三个儿子,那么不可能形成链。
所以就先这么定义,看看能不能转移。
状态转移方程
类型 0
考虑 \(f_{u,0}\) 的状态转移方程。
首先,\(u\) 点必须被炸掉,所以代价加一。
其次,炸了 \(u\) 之后,\(u\) 有几个儿子就需要再连几条边,因为最后要形成链,所以代价加上 \(u\) 的儿子数量。
最后,你还需要把儿子节点的信息传递上来,由于炸了 \(u\) 之后,\(u\) 和它的所有儿子都不联通,那么 \(u\) 的儿子的类型是几并不重要,那么代价还需要加上 \(\sum\limits_{v\in son_u } \min(f_{v,0}-1, f_{v,1}, f_{v,2})\)
为什么有一项是 \(f_{v,0}-1\)?为啥要减一?因为在之前遍历到 \(v\) 的时候,\(u,v\) 之间的边被炸了一次;现在炸 \(u\) 的时候,\(u,v\) 之间的边又被炸了一次,重复了。
我们令 \(d_u\) 表示 \(u\) 的儿子的数量,那么 \(f_{u,0} = \sum\limits_{v\in son_u } \min(f_{v,0}-1, f_{v,1}, f_{v,2}) + d_u + 1\)
类型 1
首先,\(u\) 不能被炸,如果让 \(u\) 只剩下 \(1\) 个儿子,我们可以来一个简单的容斥。
先把 \(u\) 的所有儿子都炸掉,然后选择一个儿子恢复,当然有可能不选,因为是最多一个儿子。
考虑第一步,代价很简单,为 \(\sum\limits_{v\in son_u} f_{v,0}\)
对于第二步,我们要挑选一个 \(v\),先将代价减去 \(f_{v,0}\) ,表示我不炸这个 \(v\) 了,让它留着做 \(u\) 的儿子;再将代价加上 \(f_{v,1}\),表示将信息转移到父亲,至于为什么和 \(f_{v,2}\) 没有关系,后面再说。
所以儿子都炸完之后,我们要找一个最大的 \(f_{v,0} - f_{v,1}\),让原来的代价减去它,即为最终代价,如果所有的 \(f_{v,0} - f_{v,1}\) 都小于零,那就不要儿子了,因为要上儿子只能使代价变大。
为什么和 \(f_{v,2}\) 没有关系?因为不可能由 \(f_{v,2}\) 转移过来,因为一个点有一个儿子,而这个儿子又有两个儿子,那么肯定不可能组成一条链,如果还不懂的话,我画个图:
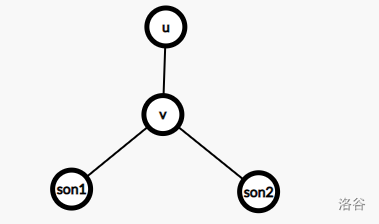
所以状态转移方程为:\(f_{u,1} = \sum\limits_{v\in son_u} f_{v,0} - \max(0, \max_{v\in son_u}(f_{v,0} - f_{v,1}))\)
类型 2
这个简单,在类型 1 的基础上再减去一个次大的大于零的 \(f_{v,0} - f_{v,1}\) 即可。
即 \(f_{u,2} = f_{u,1} - \max(0, SEC_{v \in son_u}(f_{v,0} - f_{v,1}))\) (这里的 \(SEC\) 指第二大的数)
整理
\(f_{u,0} = \sum\limits_{v\in son_u } \min(f_{v,0}-1, f_{v,1}, f_{v,2}) + d_u + 1\)
\(f_{u,1} = \sum\limits_{v\in son_u} f_{v,0} - \max(0, \max_{v\in son_u}(f_{v,0} - f_{v,1}))\)
\(f_{u,2} = f_{u,1} - \max(0, SEC_{v \in son_u}(f_{v,0} - f_{v,1}))\)
求答案
首先对于每一棵树,我们的答案很显然:为 \(\min(f_{u,0}, f_{u,1}, f_{u,2})\),但这是一个森林,所以我们还需要加上一些边让整森林变成一颗大树,加边数量为:\(n-1-m\),即总共需要 \(n-1\) 条边,题目给了 \(m\) 条边,那么还需要再加上 \(n-1-m\) 条边
所以 \(Ans = \sum\limits_{u\in root} \min(f_{u,0}, f_{u,1}, f_{u,2}) + n - 1 - m\)
code
#include <iostream>
#include <cstring>
using namespace std;
const int N = 2e6 + 10, M = 2 * N;
int n, m, ans;
int h[N], e[M], ne[M], idx;
int d[N], f[N][3];
bool vis[N];
int read()
{
int s = 0, w = 1;
char c = getchar();
while (c < '0' || c > '9')
{
if (c == '-') w = -1;
c = getchar();
}
while (c >= '0' && c <= '9')
{
s = s * 10 + c - '0';
c = getchar();
}
return s * w;
}
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++ ;
return;
}
void dfs(int u)
{
vis[u] = true;
int fir = 0, sec = 0;
for (int i = h[u]; ~i; i = ne[i])
{
int ver = e[i];
if (vis[ver]) continue;
dfs(ver);
int delta = f[ver][0] - f[ver][1];
if (delta > fir) sec = fir, fir = delta;
else if (delta > sec) sec = delta;
f[u][0] += min(f[ver][0] - 1, min(f[ver][1], f[ver][2]));
f[u][1] += f[ver][0];
}
f[u][0] += d[u] + 1;
f[u][1] -= fir;
f[u][2] = f[u][1] - sec;
return;
}
int main()
{
n = read(), m = read();
ans = (n - 1) - m;
memset(h, -1, sizeof h);
for (int i = 1; i <= m; i ++ )
{
int a, b;
a = read(), b = read();
add(a, b);
add(b, a);
d[a] ++ ;
d[b] ++ ;
}
for (int i = 1; i <= n; i ++ )
{
if (!vis[i])
{
dfs(i);
ans += min(f[i][0], min(f[i][1], f[i][2]));
}
}
cout << ans << endl;
return 0;
}
/*
_____
/ \
/ 'v' \
/ __O__ \
\____|____/
*/
完结撒花!
标签:02,炸掉,洛谷,int,题解,sum,son,儿子,代价 From: https://www.cnblogs.com/LittleMoMol-kawayi/p/solution_LuoGu_P8595.html